
Condiții de echilibru translațional, exemple, exerciții
Se pretinde că se află un obiect echilibru translațional când suma forțelor care acționează asupra ei este zero. Acest lucru nu înseamnă că există neapărat odihnă, dar mișcarea, dacă există, ar fi uniformă rectilinie sau exclusiv rotațională, în cazul unui obiect mare..
Condițiile de echilibru mecanic se bazează pe Legile mecanicii lui Newton. Într-adevăr, prima lege ne spune că un obiect este în repaus sau se mișcă cu o mișcare rectilinie uniformă MRU, cu condiția să nu acționeze o forță netă asupra acestuia.

Acum, forța netă sau forța rezultantă este pur și simplu suma vectorială a tuturor forțelor care acționează asupra obiectului. Conform celei de-a doua legi a lui Newton, această sumă trebuie să fie egală cu produsul dintre masă și accelerație, dar dacă obiectul nu este accelerat, această sumă dispare.
Și în absența accelerației, există cele două posibilități menționate anterior: corpul este în repaus, adică nu se mișcă sau, dacă se întâmplă, trebuie să fie cu MRU. În primul caz vorbim de echilibru transnațional static, iar în al doilea, dinamic.
Echilibrul translațional este un factor important în multe aspecte ale ingineriei, de exemplu în construcții. Elementele care alcătuiesc o clădire: grinzi, cabluri, cadre și multe altele, trebuie să fie în echilibru pentru a garanta stabilitatea incintei.
Echilibrul translațional este căutat și în structurile mobile, cum ar fi scările rulante, benzile transportoare și în practicarea a numeroase sporturi..
Indice articol
- 1 Condiția echilibrului translațional
- 1.1 Diagrame cu corp liber
- 2 Exemple de echilibru translațional
- 2.1 Clădiri și drumuri
- 2.2 Cărți și obiecte pe rafturi
- 2.3 Mobila
- 2.4 Semafoare
- 2.5 Iluminatul public
- 3 Exercițiul a fost rezolvat
- 3.1 Soluție
- 4 Referințe
Condiție de echilibru translațional
Să presupunem că mai multe forțe acționează asupra unui corp, pe care le denumim ca fiind F1, FDouă, F3... . Fn, folosind tipul aldin pentru a evidenția faptul că forțele sunt vectori și trebuie adăugate ca atare.
Suma vectorială a tuturor acestor forțe se numește forță rezultantă sau forta neta. Dacă această însumare are ca rezultat vectorul nul, condiția pentru echilibrul translațional este îndeplinită:
F1+ FDouă+ F3... .+ Fn = 0
Această condiție poate fi scrisă compact folosind notația de însumare:
∑ Feu = 0
În ceea ce privește componentele forței rezultante, ecuația de mai sus, care este vectorială, poate fi împărțită în trei ecuații scalare, una pentru fiecare componentă a forței rezultante:
∑ Fix = 0; ∑ FDa = 0 și ∑ Fz = 0
În practică, nu este ușor să anulați suma forțelor, deoarece fricțiunea este o forță de contact între suprafețe care este cu greu anulată complet de orice altă forță..
Acesta este motivul pentru care obiectele reale nu sunt aproape niciodată scutite de forțele externe și, în consecință, este dificil să se obțină un echilibru translațional.
Astfel, inginerii folosesc mecanisme pentru a reduce frecarea, cum ar fi rulmenții și utilizarea uleiurilor lubrifiante..
Diagrame cu corp liber
Diagrama corpului liber este o diagramă în care sunt trasate forțele care acționează asupra corpului. Când se caută un echilibru translațional, aceste forțe trebuie să fie echilibrate. De exemplu, dacă acționează o forță verticală îndreptată în jos, cum ar fi greutatea, atunci trebuie să existe o forță verticală în sus care să aibă exact aceeași magnitudine.
Această forță poate fi furnizată de mâna care susține obiectul astfel încât să nu cadă, o frânghie sau pur și simplu suprafața unei mese.
Dacă există o forță tangențială la suprafață, cum ar fi frecare cinetică sau statică, trebuie să existe o altă forță opusă pentru ca echilibrul să existe. De exemplu, să ne uităm la greutatea atârnată de corzile prezentate în figura următoare.
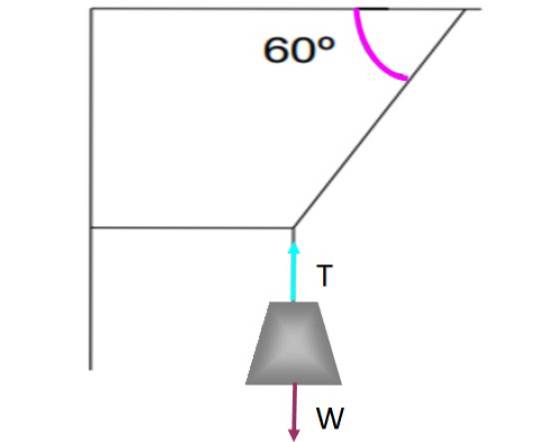
Greutatea este menținută în echilibru translațional și fără mișcare, datorită frânghiei verticale care o ține exercitând o tensiune T care compensează greutatea W. Fiecare forță a fost reprezentată pe greutate printr-o săgeată, fiecare de dimensiuni egale și cu aceeași direcție, dar direcție opusă..
Forța de echilibrare
Să presupunem că un set de forțe acționează asupra unui obiect. Aceasta se numește a sistemul de forță din care rezultatul poate fi găsit așa cum s-a explicat mai sus: prin adăugarea vectorială a fiecărei forțe a sistemului.
Ei bine, se numește forța opusă acestui rezultat forța de echilibrare. Dacă forța rezultată este FR iar forța de echilibrare este ȘI, atunci:
ȘI + FR = 0
Prin urmare:
ȘI = - FR
Exemple de echilibru translațional
Multe obiecte pe care le găsim zilnic, în interiorul și în afara casei, se află în echilibru translațional:
Clădiri și drumuri
Clădirile și drumurile sunt construite pentru a rămâne stabile și a nu se răsturna sau a prăbuși. Cu toate acestea, în zgârie-nori și, în general, în clădiri foarte înalte, este necesară o anumită flexibilitate pentru a rezista acțiunii vântului..
Cărți și obiecte pe rafturi
Cărțile dintr-o bibliotecă și produsele de pe rafturile magazinelor sunt obiecte care rămân în echilibru translațional și nu se mișcă..
Mobila
Mobilierul, televizorul cu ecran plat și imaginile de pe perete, precum și lămpile agățate de tavan, ca să menționăm câteva obiecte, sunt în echilibru translațional..
Semafor
Semaforele sunt fixate de stâlpi și cabluri, astfel încât să nu cadă. Știm totuși că vântul îi face să se legene.
Iluminat public
Farurile sunt, de asemenea, în echilibru translațional, fixate pe stâlpi, cum ar fi farul din imaginea principală..
Exercițiul a fost rezolvat
Cât de mare trebuie să fie forța Fs de frecare statică astfel încât caseta din figură să rămână în repaus la mijlocul planului înclinat la un unghi α de 37º? Masa cutiei este m = 8 kg.
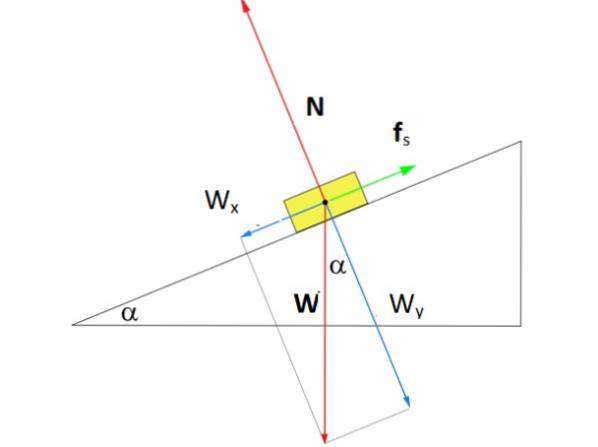
Soluţie
Figura arată schema corpului liber al cutiei de pe plan. Există trei forțe care acționează asupra sa: greutatea W, direcționat vertical în jos, normalul N, care este forța perpendiculară exercitată de suprafața planului asupra cutiei și, în cele din urmă, forța statică de frecare Fs ceea ce se opune cutiei care alunecă în jos.
Condiția de echilibru translațional afirmă că:
W + N + Fs = 0
Dar trebuie să ne amintim că aceasta este o sumă vectorială și pentru a o realiza este necesară descompunerea forțelor în componente de-a lungul axelor de coordonate.
În figură a fost desenat un sistem de coordonate în care axa x rulează paralel cu suprafața planului înclinat. Cu această alegere, fricțiunea statică cade pe axa menționată, în timp ce normalul este pe axa y. Greutatea este singura forță înclinată și trebuie descompusă cu ajutorul trigonometriei:
WX = W. sin α
WDa = W. cos α
Suma forțelor de-a lungul fiecărei axe este:
∑ FDa = N - WDa = 0
∑ FX = fs - WX = 0
Din această ultimă ecuație rezultă că:
Fs = WX
Și ca WX = W. sin α și magnitudinea greutății la rândul său este W = m.g, unde g este valoarea greutății, atunci magnitudinea fricțiunii statice este pur și simplu:
Fs = m⋅g⋅sen α = 8 kg × 9,8 m / sDouă × sin 37º = 47,2 N.
Referințe
- Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill.
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 2. Dinamica. Editat de Douglas Figueroa (USB).
- Giambattista, A. 2010. Fizică. Al 2-lea. Ed. McGraw Hill.
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7ma. Ed. Cengage Learning.
- Tippens, P. 2011. Fizică: concepte și aplicații. Ediția a VII-a. Dealul Mcgraw.



Nimeni nu a comentat acest articol încă.