
Istoricul statisticilor descriptive, caracteristici, exemple, concepte
Statisticile descriptive este ramura Statisticii care este responsabilă pentru colectarea și organizarea informațiilor despre comportamentul sistemelor cu multe elemente, cunoscute generic sub numele de populației.
Pentru a face acest lucru, folosește tehnici numerice și grafice, prin care prezintă informații, fără a face predicții sau inferențe despre populația din care provine..

Indice articol
- 1 Istorie
- 1.1 Epoca antică
- 1.2 Renașterea
- 1.3 Epoca Modernă
- 2 Caracteristicile statisticii descriptive
- 3 La ce servește statisticile descriptive?
- 3.1 Economie
- 3.2 Fizică și mecanică
- 3.3 Medicină
- 3.4 Nutriție
- 4 Exemple de statistici descriptive
- 4.1 Exemplul 1
- 4.2 Exemplul 2
- 4.3 Exemplul 3
- 5 Concepte de bază ale statisticii descriptive
- 5.1 Populația
- 5.2 Eșantion
- 5.3 Variabilă
- 5.4 Măsuri ale tendinței centrale
- 5.5 Măsurători ale dispersiei
- 6 Subiecte de interes
- 7 Referințe
Poveste
In varsta
Statistica își are originea în nevoia umană de a organiza informațiile necesare supraviețuirii și bunăstării sale, precum și de a anticipa evenimentele care o afectează. Marile civilizații ale antichității au lăsat evidențe ale coloniștilor, impozitelor colectate, cantitatea de recolte și mărimea armatelor.
De exemplu, în timpul lungii sale domnii, Ramses al II-lea (1279-1213 î.Hr.) a ordonat recensământul pământurilor și locuitorilor din Egipt, care până atunci avea în jur de 2 milioane de locuitori.
La fel, Biblia povestește că Moise a efectuat un recensământ pentru a afla câți soldați aveau cele douăsprezece triburi ale lui Israel.
De asemenea, în Grecia antică erau numărați oameni și resurse. Romanii, remarcabili prin organizarea lor înaltă, înregistrau periodic populația, întocmind recensământuri la fiecare cinci ani, inclusiv teritorii și resurse..
Renaştere
După declinul Romei, înregistrările statistice importante au fost rare, până la venirea Renașterii, când Statistica a reapărut ca un ajutor în luarea deciziilor.
La sfârșitul secolului al XVII-lea, s-a născut teoria probabilităților, rezultatul înclinației oamenilor pentru jocurile de noroc, care i-au conferit Statisticii rigoarea matematică care a făcut din ea o știință în sine..
Epoca modernă
Un nou impuls a venit cu teoria erorilor și a celor mai mici pătrate în secolul al XIX-lea, care a fost urmată de metoda corelației dintre variabile, pentru a evalua cantitativ relația dintre ele..
Până în cele din urmă, în secolul al XX-lea, statisticile s-au răspândit în fiecare ramură a științei și ingineriei ca instrument indispensabil în rezolvarea problemelor..
Caracteristici statistice descriptive
Statisticile descriptive se caracterizează prin:
- Organizați informațiile colectate sub formă de date și grafice. Graficele pot fi diverse: histograme, poligoane de frecvență, diagrame în formă de plăcintă, printre altele..
- Distribuiți datele în intervale de frecvență pentru a facilita gestionarea acestora. Folosiți aritmetica pentru a găsi cele mai reprezentative valori ale datelor, prin măsuri de tendință centrală, precum și pentru a analiza dispersia acestora.
- Determinați forma distribuțiilor, simetria lor, dacă sunt centrate sau înclinate și dacă sunt ascuțite sau mai degrabă turtite.
La ce servește statisticile descriptive?
Ori de câte ori datele trebuie colectate, organizate și prezentate, statisticile descriptive sunt esențiale în domeniile științei care se ocupă de multe elemente și cantități, precum și în mare parte din activitățile umane: economie, politică, sănătate, sport și multe altele..
Aici sunt cateva exemple:
Economie
Statisticile descriptive se referă la înregistrarea și organizarea consecventă a datelor despre populații și vârstele, veniturile, investițiile, veniturile și cheltuielile acestora. În acest fel, guvernele și instituțiile planifică îmbunătățiri și investesc resursele în mod corespunzător..
Cu ajutorul acestuia, achizițiile, vânzările, returnările și eficiența serviciilor sunt monitorizate. Din acest motiv, statisticile sunt esențiale în luarea deciziilor.
Fizică și mecanică
Fizica și mecanica folosesc statisticile pentru a studia mediile continue, care constau dintr-un număr mare de particule, cum ar fi atomii și moleculele. Se pare că nu este posibil să le urmăriți separat..
Dar studiind comportamentul global al sistemului (o porțiune de gaz, de exemplu) din punct de vedere macroscopic, este posibil să se găsească medii și să se definească variabile macroscopice pentru a le cunoaște proprietățile. Un exemplu în acest sens este teoria cinetică a gazelor.
Medicament
Este un instrument esențial atunci când se monitorizează bolile, de la originile lor și pe parcursul evoluției lor, precum și eficacitatea tratamentelor.
Statisticile care descriu ratele de morbiditate, ratele de vindecare, incubația sau timpii de dezvoltare a unei boli, vârsta la care apare de obicei și date similare, sunt necesare atunci când se proiectează cele mai eficiente tratamente..
Nutriție
Una dintre numeroasele aplicații ale statisticilor descriptive este de a înregistra și comanda date despre consumul de alimente în diferite populații: cantitatea, calitatea și care sunt cele mai consumate, printre multe alte observații care interesează experții..
Exemple de statistici descriptive
Iată câteva exemple care ilustrează cât de utile sunt instrumentele statistice descriptive pentru a lua decizii:
Exemplul 1

Autoritățile educaționale ale unei țări planifică îmbunătățiri instituționale. Să presupunem că veți implementa un nou sistem de cantină școlară.
Pentru aceasta, este necesar să aveți date despre populația studențească, de exemplu numărul de elevi pe clasă, vârsta, sexul, înălțimea, greutatea și statutul socio-economic. Aceste informații sunt apoi prezentate sub formă de tabele și grafice..
Exemplul 2
Pentru a ține evidența echipei locale de fotbal și a face noi semnături, managerii țin evidența numărului de jocuri jucate, câștigate, egalate și pierdute, precum și a numărului de goluri, a marcatorilor și a modului în care au reușit să înscrie: lovitură liberă, jumătate instanță, penalități, cu piciorul stâng sau drept, printre alte detalii.
Exemplul 3
O înghețată are mai multe arome de înghețată și dorește să-și îmbunătățească vânzările, de aceea proprietarii efectuează un studiu în care numără numărul clienților, îi separă pe grupe după sex și interval de vârstă.
În acest studiu, se înregistrează, de exemplu, aroma preferată de înghețată și cea mai bine vândută prezentare. Iar cu datele colectate, ei planifică achizițiile de arome și recipientele și accesoriile necesare pregătirii lor..
Bazele statisticii descriptive
Aceste concepte fundamentale sunt necesare pentru aplicarea tehnicilor statistice, să vedem:
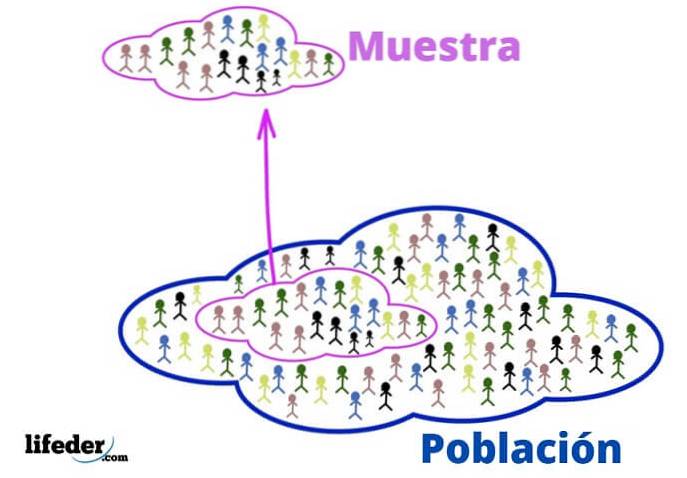
Populația
În contextul statistic, populația se referă la universul sau grupul din care provin informațiile.
Nu sunt întotdeauna legate de oameni, deoarece pot fi grupuri de animale, plante sau obiecte precum mașini, atomi, molecule și chiar evenimente și idei..
Spectacol
Atunci când populația este foarte mare, se extrage un eșantion reprezentativ din acesta și se analizează, fără a pierde informații relevante..
Poate fi ales la întâmplare sau conform unor criterii stabilite anterior de analist. Avantajul este că, fiind un subset al populației, este mult mai ușor de gestionat.
Variabil
Se referă la setul de valori pe care le poate lua o anumită caracteristică a populației. Un studiu poate conține mai multe variabile, cum ar fi vârsta, sexul, greutatea, nivelul academic, starea civilă, venitul, temperatura, culoarea, timpul și multe altele.
Variabilele pot fi de natură diferită, deci există criterii pentru a le clasifica și a le oferi cel mai adecvat tratament.
Variabile categorice și variabile numerice
În funcție de modul în care sunt măsurate, variabilele pot fi:
-Categoric
-Numeric
Variabile categorice, numite și calitativ, reprezintă calități precum starea civilă a unei persoane, care poate fi singură, căsătorită, divorțată sau văduvă.
În schimb, variabile numerice sau cantitativ, pot fi măsurate, cum ar fi vârsta, timpul, greutatea, venitul și multe altele.
Variabile discrete și variabile continue
Variabilele discrete iau doar valori discrete, așa cum sugerează și numele lor. Exemple dintre acestea sunt numărul de copii dintr-o familie, câți subiecți sunt într-un anumit curs și numărul de mașini dintr-o parcare.
Aceste variabile nu iau întotdeauna valori întregi, deoarece există și fracționare.
Pe de altă parte, variabilele continue admit valori infinite într-un anumit interval, cum ar fi greutatea unei persoane, pH-ul sângelui, timpul unei consultații telefonice și diametrul mingilor de fotbal..
Măsuri de tendință centrală
Ele dau o idee despre tendința generală urmată de date. Vom menționa cele mai utilizate trei măsuri centrale:
-Jumătate
-Median
-Modă
Jumătate
Echivalent cu media valorilor. Se calculează prin adăugarea tuturor observațiilor și împărțirea la numărul total:

Modă
Este valoarea care se repetă cel mai mult într-un set de date, cea mai frecventă sau cea mai frecventă, deoarece într-o distribuție poate exista mai mult de un mod.
Median
Când sortați un set de date, mediana este valoarea centrală a tuturor acestora.
Măsuri de dispersie
Ele subliniază variabilitatea datelor și dau o idee despre cât de departe sau de împrăștiate sunt de măsurile centrale. Cele mai utilizate sunt:
Rang
Este diferența dintre cea mai mare valoare xM iar cel mai mic xm dintr-un set de date:
Rang = xM - Xm
Varianța
Măsurează cât de departe sunt datele de valoarea medie. Pentru a face acest lucru, se face o medie, dar cu diferențele dintre orice valoare xeu și media, pătrat pentru a le împiedica să se anuleze reciproc. De obicei se notează cu litera greacă σ pătrat sau cu sDouă:

Varianța nu are aceleași unități ca datele, deci abaterea standard este definită ca rădăcina pătrată a varianței și este notată ca σ sau s:

În loc să țineți cont de fiecare dată în mod individual, este de preferat să le grupați în intervale, ceea ce facilitează munca, mai ales dacă există multe valori. De exemplu, atunci când lucrați cu copii într-o școală, aceștia pot fi grupați în categorii de vârstă: 0 la 6 ani, 6 la 12 ani și 12 la 18 ani.
Diagramele
Acestea sunt o modalitate excelentă de a vedea distribuția datelor dintr-o privire și conțin toate informațiile culese în tabele și tabele, dar mult mai accesibile.
Există o mare varietate a acestora: cu bare, liniare, circulare, stem și frunze, histograme, poligoane de frecvență și pictograme. Exemple de grafice statistice sunt prezentate în Figura 3..
Teme de interes
Ramuri de statistici.
Variabile statistice.
Populație și eșantion.
Statistici deduse.
Referințe
- Faraldo, P. Statistică și metodologie de cercetare. Recuperat de pe: eio.usc.es.
- Fernández, S. 2002. Statistici descriptive. Al 2-lea. Ediție. Editorial ESIC. Recuperat din: Google Cărți.
- Istoria Statisticii. Recuperat de pe: eumed.net.
- Ibañez, P. 2010. Matematică II. Abordarea competențelor. Cengage Learning.
- Monroy, S. 2008. Statistici descriptive. Primul. Ediție. Institutul Politehnic Național din Mexic.
- Formulele Universului. Statisticile descriptive. Recuperat de pe: universoformulas.com.



Nimeni nu a comentat acest articol încă.