Se vorbește despre experiment aleatoriu atunci când rezultatul fiecărui proces particular este imprevizibil, chiar dacă poate fi stabilită probabilitatea apariției unui anumit rezultat.
Cu toate acestea, trebuie clarificat faptul că nu este posibil să se reproducă același rezultat al unui sistem aleatoriu cu aceiași parametri și condiții inițiale în fiecare test al experimentului..
Un bun exemplu de experiment aleatoriu este rostogolirea unei matrițe. Chiar dacă se are grijă să arunci matrița în același mod, fiecare încercare va produce un rezultat imprevizibil. De fapt, singurul lucru care se poate spune este că rezultatul poate fi unul dintre următoarele: 1, 2, 3, 4, 5 sau 6.
Aruncarea unei monede este un alt exemplu de experiment aleatoriu cu doar două rezultate posibile: capete sau cozi. Deși moneda este aruncată de la aceeași înălțime și în același mod, factorul șansă va fi întotdeauna prezent, rezultând incertitudine la fiecare nouă încercare..
Opusul unui experiment aleatoriu este un experiment determinist. De exemplu, se știe că de fiecare dată când apa este fiartă la nivelul mării, temperatura de fierbere este de 100 ° C. Dar nu se întâmplă niciodată ca, păstrând aceleași condiții, rezultatul să fie uneori de 90 ° C, altele 12 0 ° C și alteori 100 ° C..
Indice articol
Se numește setul tuturor rezultatelor posibile ale unui experiment aleatoriu spațiu de probă. În experimentul aleatoriu al aruncării unei matrițe, spațiul eșantionului este:
D = 1, 2, 3, 4, 5, 6.
Pe de altă parte, în aruncarea unei monede spațiul eșantionului este:
M = capete, ștampilă.
Într-un experiment aleatoriu, a eveniment este apariția sau nu a unui anumit rezultat. De exemplu, în cazul unei aruncări de monede, un eveniment sau o întâmplare este că se ridică.
Un alt eveniment dintr-un experiment aleatoriu ar putea fi următorul: că un număr mai mic sau egal cu trei este aruncat pe rolul unei matrițe.
În cazul în care apare evenimentul, atunci setul de rezultate posibile este setul:
E = 1, 2, 3
La rândul său, acesta este un subset al spațiului sau setului de probă:
M = 1, 2, 3, 4, 5, 6.
Iată câteva exemple care ilustrează cele de mai sus:
Să presupunem că două monede sunt aruncate, una după alta. Întrebă:
a) Indicați dacă este un experiment aleatoriu sau, dimpotrivă, un experiment determinist.
b) Care este spațiul eșantion S al acestui experiment?
c) Indicați setul evenimentului A, corespunzător faptului că experimentul are ca rezultat capete și cozi.
d) Calculați probabilitatea ca evenimentul A să apară.
e) În cele din urmă, găsiți probabilitatea ca evenimentul B să apară: în rezultat nu apar capete.
a) Este un experiment aleatoriu, deoarece nu există nicio modalitate de a prezice care va fi rezultatul unei aruncări a celor două monede.
b) Spațiul eșantion este ansamblul tuturor rezultatelor posibile:
S = (c, c), (c, s), (s, c), (s, s)
c) Evenimentul A, dacă are loc, poate avea următoarele rezultate:
A = (c, s), (s, c)
d) Probabilitatea apariției evenimentului A se obține prin împărțirea numărului de elemente ale mulțimii A la numărul de elemente ale mulțimii S corespunzător spațiului eșantion:
P (A) = 2/4 = ½ = 0,5 = 50%
e) Setul de rezultate posibile care corespund evenimentului B (care nu apar capete în rezultat) este:
B = (s, s)
Prin urmare, probabilitatea ca evenimentul B să apară într-un proces este coeficientul dintre numărul de rezultate posibile ale lui B și numărul total de cazuri:
P (B) = ¼ = 0,25 = 25%.
O pungă conține 10 baloane albe și 10 baloane negre. Trei bile consecutiv sunt scoase din pungă la întâmplare și fără a privi înăuntru.
a) Determinați spațiul eșantionului acestui experiment aleatoriu.
b) Determinați setul de rezultate corespunzătoare evenimentului A, care constă în a avea două marmuri negre după experiment.
c) Evenimentul B este de a obține cel puțin două marmuri negre, determinați setul B de rezultate pentru acest eveniment.
d) Care este probabilitatea ca evenimentul A să apară?
e) Aflați probabilitatea ca evenimentul B să apară.
f) Determinați probabilitatea ca rezultatul experimentului aleatoriu să fie că aveți cel puțin o marmură neagră. Acest eveniment se va numi C.
Pentru a construi spațiul de eșantionare, este util să realizați o diagramă arborescentă, ca cea prezentată în Figura 3:
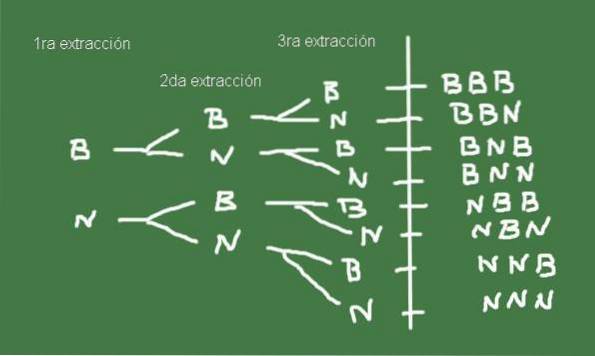
Setul Ω al posibilelor rezultate ale extragerii a trei bile dintr-o pungă cu același număr de bile alb-negru, este tocmai spațiul eșantionului acestui experiment.
Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)
Setul de rezultate posibile corespunzător evenimentului A, care constă în a avea două bile negre este:
A = (b, n, n), (n, b, n), (n, n, b)
Evenimentul B este definit ca: „având cel puțin două bile negre după ce a desenat aleator trei dintre ele”. Setul de rezultate posibile pentru evenimentul B este:
B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)
Probabilitatea de a avea evenimentul A este coeficientul dintre numărul de rezultate posibile pentru acest eveniment și numărul total de rezultate posibile, adică numărul de elemente din spațiul eșantion.
P (A) = n (A) / n (Ω) = 3/8 = 0,375 = 37,5%
Deci, există o șansă de 37,5% de a avea două bile negre după ce au extras aleatoriu trei bile din geantă. Dar rețineți că în niciun caz nu putem prezice rezultatul exact al experimentului.
Probabilitatea apariției evenimentului B, constând în obținerea a cel puțin unei marmuri negre este:
P (B) = n (B) / n (Ω) = 4/8 = 0,5 = 50%
Aceasta înseamnă că posibilitatea apariției evenimentului B este egală cu probabilitatea ca acesta să nu aibă loc.
Probabilitatea de a obține cel puțin o marmură neagră, după extragerea a trei dintre ele, este egală cu 1 minus probabilitatea ca rezultatul să fie „cele trei marmuri albe”.
P (C) = 1 - P (b b b) = 1 - ⅛ = ⅞ = 0,875 = 87,5%
Acum, putem verifica acest rezultat, observând că numărul posibilităților pe care le are evenimentul C este egal cu numărul de elemente ale rezultatelor posibile pentru evenimentul C:
C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)
n (C) = 7
P (C) = n (C) / n (Ω) = ⅞ = 87,5%
Nimeni nu a comentat acest articol încă.