
Factor comun prin gruparea de termeni exemple, exerciții

factor comun prin gruparea termenilor este o procedură algebrică care vă permite să scrieți câteva expresii algebrice sub formă de factori. Pentru a atinge acest obiectiv, este mai întâi necesar să grupați expresia în mod corespunzător și să observați că fiecare grup astfel format are, de fapt, un factor comun.
Aplicarea corectă a tehnicii necesită o anumită practică, dar în scurt timp o puteți stăpâni. Să vedem mai întâi un exemplu ilustrativ descris pas cu pas. Apoi, cititorul poate aplica ceea ce a învățat în fiecare dintre exercițiile care vor apărea mai târziu.

De exemplu, să presupunem că trebuie să luați în calcul următoarea expresie:
2xDouă + 2xy - 3zx - 3zy
Această expresie algebrică constă din 4 monomii sau termeni, separați prin semne + și -, și anume:
2xDouă, 2xy, -3zx, -3zy
Privind cu atenție, x este comun pentru primele trei, dar nu pentru ultimul, în timp ce y este comun pentru al doilea și al patrulea și z este comun pentru al treilea și al patrulea..
Deci, în principiu, nu există un factor comun pentru cei patru termeni în același timp, dar dacă aceștia sunt grupați așa cum se va arăta în secțiunea următoare, este posibil să apară unul care să ajute la scrierea expresiei ca produsul a doi sau mai mulți factori.
Indice articol
- 1 Exemple
- 2 Întrebări importante despre factorul comun prin grupare
- 3 Exerciții
- 3.1 - Exercițiul 1
- 3.2 - Exercițiul 2
- 4 Referințe
Exemple
Factorizați expresia: 2xDouă + 2xy - 3zx - 3zy
Pasul 1: grup
2xDouă + 2xy - 3zx - 3zy = (2xDouă + 2xy) + (-3zx - 3zy)
Pasul 2: Găsiți factorul comun al fiecărui grup
2xDouă + 2xy - 3zx - 3zy =
= (2xDouă + 2xy) - (3zx + 3zy) =
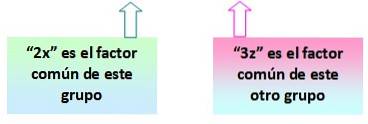
= 2x (x + y) - 3z (x + y)
Euimportant: semnul negativ este, de asemenea, un factor comun care trebuie luat în considerare.
Acum rețineți că parantezele (x + y) se repetă în cei doi termeni obținuți prin grupare. Acesta este factorul comun care se căuta.
Pasul 3: luați în calcul întreaga expresie
2xDouă + 2xy - 3zx - 3zy = (x + y) (2x - 3z)
Cu rezultatul anterior, s-a atins obiectivul factorizării, care nu este altul decât transformarea unei expresii algebrice bazate pe adunări și scăderi de termeni, în produsul a doi sau mai mulți factori, în exemplul nostru, al: (x + y) y (2x - 3z).
Întrebări importante despre factorul comun prin grupare
Numărul 1: Cum să știți că rezultatul este corect?
Răspuns: Proprietatea distributivă se aplică rezultatului obținut și după reducere și simplificare, expresia astfel obținută trebuie să se potrivească cu originalul, dacă nu, există o eroare.
În exemplul anterior, lucrăm invers cu rezultatul, pentru a verifica dacă este corect:
(x + y) (2x - 3z) = 2xDouă -3zx + 2xy - 3zy
Deoarece ordinea completărilor nu modifică suma, după aplicarea proprietății distributive se returnează toți termenii originali, semnele incluse, prin urmare, factorizarea este corectă.
Intrebarea 2: Ar fi putut fi grupate în alt mod?
Răspuns: Există expresii algebrice care permit mai multe forme de grupare și altele care nu. În exemplul selectat, cititorul poate încerca singur alte posibilități, de exemplu grupând astfel:
2xDouă + 2xy - 3zx - 3zy = (2xDouă- 3zx) + (2xy - 3zy)
Și puteți verifica dacă rezultatul este același cu cel obținut aici. Găsirea grupării optime este o chestiune de practică.
Întrebarea 3: De ce este necesar să se ia un factor comun dintr-o expresie algebrică?
Răspuns: Pentru că există aplicații în care expresia factorizată face calculele mai ușoare. De exemplu, să presupunem că doriți să faceți 2xDouă + 2xy - 3zx - 3zy egal cu 0. Care ar fi posibilitățile?
Pentru a răspunde la această întrebare, versiunea factorizată este mult mai utilă decât dezvoltarea inițială în termeni. Se spune astfel:
(x + y) (2x - 3z) = 0
O posibilitate ca expresia să fie 0 este că x = -y, indiferent de valoarea lui z. Iar cealaltă este că x = (3/2) z, indiferent de valoarea lui y.
Instruire
- Exercitiul 1
Luați un factor comun al următoarei expresii prin gruparea de termeni:
ax + ay + bx + by
Soluţie
Primele două sunt grupate, cu factorul comun „a” și ultimele două cu factorul comun „b”:
ax + ay + bx + by = a (x + y) + b (x + y)
Odată ce acest lucru este făcut, se dezvăluie un nou factor comun, care este (x + y), astfel încât:
ax + ay + bx + by = a (x + y) + b (x + y) = (x + y) (a + b)
Un alt mod de grupare
Această expresie susține un alt mod de grupare. Să vedem ce se întâmplă dacă termenii sunt rearanjați și se face un grup cu cei care conțin x și un altul cu cei care conțin y:
ax + ay + bx + by = ax + bx + ay + by = x (a + b) + y (a + b)
În acest fel, noul factor comun este (a + b):
ax + ay + bx + by = ax + bx + ay + by = x (a + b) + y (a + b) = (x + y) (a + b)
Ceea ce duce la același rezultat din prima grupare care a fost testată.
- Exercițiul 2
Următoarea expresie algebrică trebuie să fie scrisă ca produs al doi factori:
A treia3 - A treiaDouăb + 9abDouă-laDouă+ab-3bDouă
Soluţie
Această expresie conține 6 termeni. Să încercăm să grupăm primul și al patrulea, al doilea și al treilea și în cele din urmă al cincilea și al șaselea:
A treia3 - A treiaDouăb + 9abDouă-laDouă+ab-3bDouă = (3a3 -laDouă) + (- 3aDouăb + 9abDouă) + (ab-3bDouă)
Acum fiecare paranteză este luată în considerare:
= (3a3 -laDouă) + (- 3aDouăb + 9abDouă) + (ab -3bDouă) = aDouă (3a - 1) + 3ab (3b -a) + b (a-3b)
La prima vedere se pare că situația a fost complicată, dar cititorul nu ar trebui să fie descurajat, deoarece vom rescrie ultimul termen:
laDouă (3a - 1) + 3ab (3b -a) + b (a-3b) = aDouă (3a - 1) + 3ab (3b-a) - b (3b-a)
Ultimii doi termeni au acum un factor comun, care este (3b-a), deci pot fi luați în considerare. Este foarte important să nu pierzi din vedere primul termenDouă (3a - 1), care trebuie să însoțească în continuare totul ca adăugare, chiar dacă nu lucrați cu acesta:
laDouă (3a - 1) + 3ab (3b-a) - b (3b-a) = aDouă (3a - 1) + (3b-a) (3ab-b)
Expresia a fost redusă la doi termeni și un nou factor comun este descoperit în ultimul, care este „b”. Acum rămâne:
laDouă (3a - 1) + (3b-a) (3ab-b) = aDouă (3a - 1) + b (3b-a) (3a-1)
Următorul factor comun care apare este 3a - 1:
laDouă (3a - 1) + b (3b-a) (3a-1) = (3a - 1) [aDouă + b (3b-a)]
Sau dacă preferați fără paranteze:
(3a - 1) [aDouă + b (3b-a)] = (3a - 1) (aDouă -ab + 3bDouă)
Poate cititorul să găsească un alt mod de grupare care să ducă la același rezultat??

Referințe
- Baldor, A. 1974. Algebra elementară. Cultural Venezolana S.A.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Principalele cazuri de factoring. Recuperat de pe: julioprofe.net.
- UNAM. Matematică de bază: Factorizarea prin gruparea de termeni. Facultatea de Contabilitate și Administrație.
- Zill, D. 1984. Algebră și trigonometrie. MacGraw Hill.



Nimeni nu a comentat acest articol încă.