
Fracții tipice, exemple, exerciții rezolvate
fracțiuni sau numere fracționare sunt acele numere care sunt reprezentate prin indicarea coeficientului dintre două numere întregi la Da b, atâta timp cât b este diferit de 0. De exemplu, 1/3 este o fracție care este citită ca „o treime”.
La numărul la este cunoscut sub numele de numărător a fracției și la b Ce numitor De acelasi. Numitorul ne spune în câte părți să împărțim întregul. La rândul său, numeratorul indică câte părți din acel întreg au fost luate.

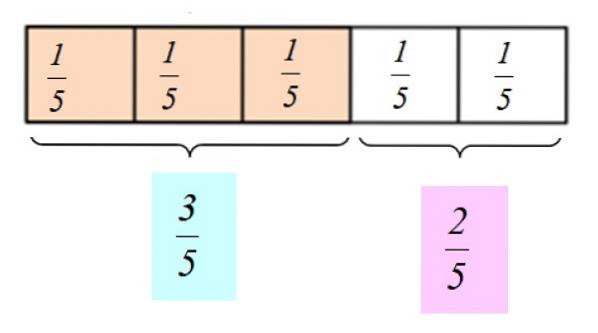
Întregul este tot ceea ce doriți să împărțiți sau să împărțiți, de exemplu, o pizza sau o ciocolată arătată în figura 1. Bara este realizată în așa fel încât este foarte ușor să o împărțiți în 5 părți egale, unde fiecare parte este echivalent 1/5 din bara completă.
În fracția sau numărul fracțional 1/5, numărătorul este 1 și numitorul este 5. Fracția este citită „o cincime”.
Să presupunem că mâncăm 3 bucăți de ciocolată. Am spune că am mâncat 3/5 părți din bar și că mai sunt 2/5 părți de împărțit cu un prieten. Putem spune, de asemenea, că am mâncat „trei cincimi din ciocolată” și i-am dat „două cincimi” prietenului nostru.
Reprezentarea grafică a acestor numere fracționare este după cum urmează:
Indice articol
- 1 Tipuri de fracții
- 1.1 fracții proprii
- 1.2 Fracțiuni necorespunzătoare
- 1.3 Fracții aparente
- 1.4 Fracții echivalente
- 1.5 Fracții ireductibile
- 1.6 Numere mixte
- 2 Exemple de fracții
- 2.1 Achiziții de alimente
- 2.2 Rețete de gătit
- 2.3 Lungimi și diametre
- 2.4 Intervalele de timp
- 3 Exerciții cu fracții
- 3.1 - Exercițiul 1
- 3.2 - Exercițiul 2
- 3.3 - Exercițiul 3
- 3.4 - Exercițiul 4
- 4 Referințe
Tipuri de fracții
Fracții adecvate
O fracție este adecvată atunci când numărătorul este mai mic decât numitorul și astfel valoarea sa este mai mică de 1. Fracțiile din secțiunea anterioară, în exemplul ciocolatei, sunt fracții proprii..
Alte exemple de fracții adecvate sunt: ½; 8/10; 3/4 și mai mult.

Fracțiuni necorespunzătoare
Numărătorul fracțiilor necorespunzătoare este mai mare decât numărătorul. De exemplu 4/3, 8/5, 21/10 aparțin acestei categorii.
Fracții aparente
Aceste fracții reprezintă un număr întreg. Printre acestea se numără 4/2, 10/5 și 27/3, deoarece dacă ne uităm cu atenție, rezultatul împărțirii numărătorului la numitorul acestor fracții dă un număr întreg.
Astfel: 4/2 = 2, 10/5 = 2 și 27/3 = 9.
Fracții echivalente
Două fracții n / m și p / q sunt echivalente atunci când împărțirea numărătorului la numitor dă aceeași cantitate. În acest fel, fracțiile echivalente reprezintă aceeași parte a întregului..
De exemplu, avem fracțiile: 15/2 și 30/4. Când împărțiți 15 la 2 obțineți 7,5, dar este la fel dacă împărțiți 30 la 4.
Pentru a afla dacă două fracții n / m și p / q sunt echivalente, se verifică următoarea egalitate:
n * q = m.p
Fracții ireductibile
Când numeratorul și numitorul sunt împărțiți la același număr și cu condiția ca rezultatul să fie un număr întreg, se obține o fracție echivalentă cu originalul, dar cu numere mai mici.
Acest proces continuă atât timp cât numeratorul și numitorul au exact același divizor. Când nu este posibil să se continue divizarea, fracțiune ireductibilă a fracției originale.
Avantajul lucrării cu fracția ireductibilă este că se obține o fracție echivalentă, dar cu numere mai mici. De aceea, atunci când lucrați cu fracțiuni, asigurați-vă că le reduceți ori de câte ori este posibil, pentru a facilita calculele..
Să presupunem că fracția 12/20, fiind numărător și numitor par, ambele pot fi împărțite la 2:
20.12 = 6/10
Și încă o dată:
6/10 = 3/5
Fracția 3/5 este echivalentă cu 12/20, dar mai simplă.
Numere mixte
O fracție necorespunzătoare admite, de asemenea, reprezentarea ca număr mixt, așa-numitul deoarece are o parte întreagă și o altă parte fracționată, partea fracțională fiind o fracție proprie..
Să vedem un exemplu rapid cu fracțiunea 15/2 despre care știm că este egală cu 7,5.
Putem exprima 15/2 ca un număr mixt ca acesta:
15/2 = 7 + 0,5
Dar 0,5 = ½. Prin urmare 15/2 = 7 ½ care scrie „șapte și jumătate”.
Exemple de fracții
Numerele fracționare sunt necesare, deoarece atât naturale cât și întregi sunt insuficiente atunci când vrem să împărțim lucruri precum bara de bomboane.
Și de aceea există o varietate infinită de modele de măsurare și obiecte ale căror specificații includ numere fracționare, fără a menționa numărul de situații cotidiene în care acestea sunt necesare..
A cumpăra alimente
În țările în care se utilizează sistemul metric, este obișnuit să se utilizeze kilogramul pentru a se referi la greutatea multor alimente. Nu dorim întotdeauna să cumpărăm cantități întregi, ci puțin mai mult sau puțin mai puțin.
De aceea întrebăm:
- ½ kg de pește
- ¾ kg de roșii
- ¼ kilogram de ceapă
- 1 ½ kg de piersici (1 Kilo și jumătate).
Și atunci când se utilizează standardele de măsurare anglo-saxone, se întâmplă același lucru: avem nevoie de 2 kilograme și jumătate sau 1/4 de kilogram de ceva.
Toate aceste numere sunt fracționate și, după cum am văzut, corespund a două tipuri diferite de fracții: proprii și improprii..
Rețete de bucătărie
Rețetele de gătit folosesc adesea numere fracționate pentru a indica cantitatea anumitor ingrediente. De exemplu:
- ½ cană de făină
- ¾ kg de zahăr pentru a pregăti un tort.
Lungimi și diametre
Dimensiunile mobilierului, pieselor textile și tot felul de ustensile de uz casnic sunt măsurate în fracțiuni de metru sau inch, indiferent dacă se utilizează sistemul metric sau anglo-saxon de măsurare zecimală..
Chiar și în țările în care sistemul metric predomină, cuprul comercial, oțelul și alte țevi de instalații sanitare vin adesea cu diametre specificate în inci. De asemenea, alte articole hardware, cum ar fi șuruburi și piulițe.
Deoarece un inch este echivalent cu 2,54 cm, aceste piese, care au diametre mai mici, sunt de obicei exprimate în fracțiuni de inch..
Măsurile foarte frecvente pentru conductele menajere sunt:
- ½ inch
- ¼ inch
- 3/8 și 5/8 inch.
Intervale de timp
Numerele fracționare sunt folosite zilnic pentru a exprima intervale de timp, cum ar fi ¼, ½ și ¾ dintr-o oră, sau chiar puțin mai mult: 1 oră și ¼ și așa mai departe.

Exerciții cu fracțiuni
- Exercitiul 1
Astăzi, Juanito a adus la școală un tort de ziua lui și vrea să-l împartă între toți prietenii săi, dar vrea să îi dea profesorului o piesă de trei ori mai mare decât cea a copiilor.
Ținând cont că sunt 24 de copii + profesorul, căruia doriți să îi dați echivalentul a trei bucăți, în câte bucăți ar trebui să tăiați tortul??
Soluţie
Dacă Juanito ar vrea doar să distribuie tortul printre prietenii săi, fiecare ar avea 1/24.
Dar, din moment ce vrea să dea o parte profesorului și că piesa este de trei ori mai mare, el ar trebui să distribuie tortul între 24 de elevi + 3 piese pentru profesor. Cu alte cuvinte, fiecărui copil îi corespund 1/27 bucăți, iar profesorul 3/27 bucăți.
În plus, dacă reducem fracțiunea 3/27, obținem că profesorul va lua 1/9 din tort.
- Exercițiul 2
O companie cu șef și trei angajați are venituri lunare de 6.000 de euro. Câți bani are fiecare persoană dacă șeful vrea să păstreze jumătate din ceea ce a câștigat?
Soluţie
Dacă șeful vrea să câștige jumătate, va trebui să păstreze 6000/2, ceea ce face 3000 €. Din ceilalți 3.000 de euro rămași este ceea ce vor trebui să distribuie cei trei angajați. Astfel, fiecare angajat va câștiga 3000/3, rezultând 1000 EUR.
- Exercițiul 3
Găsiți fracția ireductibilă din:
a) 12/18 și b) 4/11
Solutie la
În primul caz, observăm că atât numărătorul, cât și numitorul sunt pare și divizibile cu 2. Ele sunt, de asemenea, divizibile cu 3, deoarece 12 și 18 sunt multipli ai acelei cifre..
Deci putem simplifica fracția împărțind atât numărătorul, cât și numitorul fie la 2, fie la 3, ordinea este indiferentă.
Începând prin împărțirea la 2:
18.12 = 6/9
Acum observăm că atât numărătorul, cât și numitorul acestei fracțiuni echivalente sunt multipli de 3, deci împărțind ambii la această cifră:
6/9 = 2/3
Și din moment ce 2 și 3 sunt numere prime, nu mai au niciun alt divizor comun cu excepția 1. Am ajuns la fracția ireductibilă.
S-ar fi putut calcula și cel mai mare divizor comun CMP al numărătorului și numitorului. Pentru 12 și 18:
VMC (12,18) = 6.
Și apoi numeratorul și numitorul sunt împărțiți la acest număr, care este echivalent cu realizarea acestuia în etape.
Soluția b
Aici observăm că 11 este un număr prim și divizorii săi sunt 1 și 11. La rândul său, 4 admite 4, 2 și 1 ca divizori. Cu excepția 1, aceste numere nu au un divizor comun și, prin urmare, fracția 4/11 este ireductibil.
- Exercițiul 4
Indicați care este cea mai mare fracțiune din fiecare pereche:
a) ¾ și 5/4
b) 3/7 și 4/9
Solutie la
Când două fracții pozitive au același numitor, cu atât este mai mare cea care are numărătorul mai mare. Prin urmare, 5/4 este mai mare, deoarece 5> 3.
Soluția b
Dacă fracțiile n / m și p / q au numitori diferiți și ambii sunt pozitivi, criteriul de comparație este următorul:
Dacă n.q> m. p, apoi n / m> p / q
O altă opțiune este de a găsi expresia zecimală a fiecărei fracții și de a compara.
Conform primului criteriu: n = 3, m = 7, p = 4, q = 9. Prin urmare: n.q = 3 * 4 = 12 și m.p = 7 * 4 = 28.
Ca 12< 28, ocurre que 3/7 < 4/9.
Sau exprimăm fiecare fracție ca o zecimală, obținând acest lucru:
3/7 = 0,428571428 ... .
4/9 = 0,4444444444 ... .
Elipsa indică faptul că numărul de zecimale este infinit. Dar acest lucru este suficient pentru a verifica că într-adevăr, 4/9> 3/7.
Referințe
- Baldor, A. 1986. Aritmetică. Ediții și distribuții Codex.
- Carena, M. 2019. Manual de matematică. Universitatea Națională a Litoralului.
- Figuera, J. 2000. Matematică 8. Ediciones Co-Bo.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Pagina Matematică. Ce este o fracție? Recuperat de pe: themathpage.com.


Nimeni nu a comentat acest articol încă.