
Definiția funcției surjective, proprietăți, exemple
A funcția surjectivă este orice relație în care fiecare element aparținând codomainului este o imagine a cel puțin unui element al domeniului. Cunoscută și sub numele de funcție pe, fac parte din clasificarea funcțiilor în ceea ce privește modul în care elementele lor sunt legate.
De exemplu o funcție F: A → B definit de F (x) = 2x
În care se citește „F ce ziceti LA pana cand B definit de F (x) = 2x "
Este timpul să definiți seturile de început și de finalizare A și B.
A: 1, 2, 3, 4, 5 Acum valorile sau imaginile pe care fiecare dintre aceste elemente le vor afișa atunci când sunt evaluate F, vor fi elementele codomainului.
F (1) = 2
F (2) = 4
F (3) = 6
F (4) = 8
F (5) = 10
Formând astfel întregul B: 2, 4, 6, 8, 10
Se poate concluziona atunci că:
F: 1, 2, 3, 4, 5 → 2, 4, 6, 8, 10 definit de F (x) = 2x Este o funcție surjectivă
Fiecare element al codomainului trebuie să rezulte din cel puțin o operație a variabilei independente prin funcția în cauză. Nu există nicio limitare a imaginilor, un element al codomainului poate fi o imagine a mai multor elemente ale domeniului și încă încearcă una funcția surjectivă.
Imaginea prezintă 2 exemple cu funcții surjective.
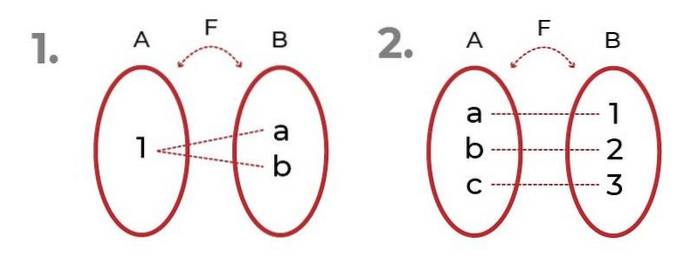
În primul se observă că imaginile pot fi referite la același element, fără a compromite surjectivitate a funcției.
În a doua vedem o distribuție echitabilă între domeniu și imagini. Acest lucru dă naștere la funcția bijectivă, unde criteriile de funcția injectivă și funcția surjectivă.
O altă metodă de identificare funcții surjective, este să verificați dacă codomainul este egal cu domeniul funcției. Aceasta înseamnă că, dacă setul de sosire este egal cu imaginile furnizate de funcție la evaluarea variabilei independente, funcția este surjectivă.
Indice articol
- 1 Proprietăți
- 1.1 Condiționarea funcției
- 2 Exemple: exerciții rezolvate
- 2.1 Exercițiul 1
- 2.2 Exercițiul 2
- 2.3 Exercițiul 3
- 2.4 Exercițiul 4
- 2.5 Exercițiul 4
- 2.6 Exercițiul 5
- 3 Exerciții propuse
- 4 Referințe
Proprietăți
A considera surjectiv pentru o funcție trebuie îndeplinite următoarele:
Fi F: DF → CF
∀ b ℮ CF ȘI la ℮ DF / F (a) = b
Acesta este modul algebric de a stabili asta pentru toate „b” care aparțin lui CF există un „a” care aparține lui DF astfel încât, funcția F evaluată în „a” este egală cu „b”.
Surjectivitatea este o particularitate a funcțiilor, în care codomainul și gama sunt similare. Astfel, elementele evaluate în funcție alcătuiesc setul de sosiri.
Condiționarea funcției
Uneori o funcție care nu este surjectiv, poate fi supus anumitor condiții. Aceste noi condiții îl pot transforma într-un funcția surjectivă.
Sunt valabile toate tipurile de modificări ale domeniului și codomainului funcției, unde obiectivul este de a îndeplini proprietățile de surjectivitate în relația corespunzătoare.
Exemple: exerciții rezolvate
Pentru a îndeplini condițiile de surjectivitate trebuie aplicate diferite tehnici de condiționare, pentru a se asigura că fiecare element al codomainului se află în setul de imagini ale funcției.
Exercitiul 1
- Să funcția F: R → R definit de linie F (x) = 8 - x
A: [Toate numerele reale]
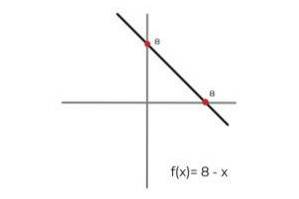
În acest caz, funcția descrie o linie continuă, care acoperă toate numerele reale atât în domeniul său, cât și în domeniul său. Deoarece gama funcției RF este egal cu codomain R Se poate concluziona că:
F: R → R definit de linie F (x) = 8 - x este un funcția surjectivă.
Acest lucru se aplică tuturor funcțiilor liniare (funcții al căror cel mai mare grad al variabilei este unul).
Exercițiul 2
- Studiază funcția F: R → R definit de F (x) = xDouă : Definiți dacă este un funcția surjectivă. Dacă nu, arătați condițiile necesare pentru ao face surjectiv.
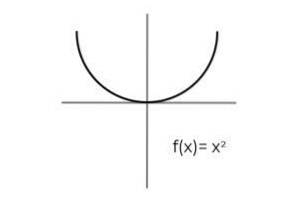
Primul lucru de luat în considerare este codomainul F, care este alcătuit din numerele reale R. Funcția nu returnează valori negative, ceea ce exclude negativele reale din imaginile posibile.
Condiționarea codomainului la intervalul [0 , ∞ ]. Este evitat să lăsați elemente ale codomainului fără legătură F.
Imaginile sunt repetate pentru perechi de elemente ale variabilei independente, cum ar fi x = 1 Da x = - 1. Dar acest lucru afectează doar injectivitate funcției, nefiind o problemă pentru acest studiu.
În acest fel se poate concluziona că:
F: R →[0, ∞ ) definit de F (x) = xDouă Este o funcție surjectivă
Exercițiul 3
- Definiți condițiile codomainului pe care le-ar face surjective la funcții
F: R → R definit de F (x) = Sen (x)
F: R → R definit de F (x) = Cos (x)
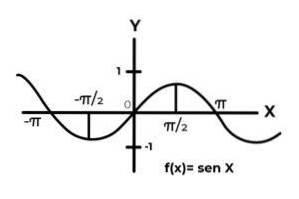
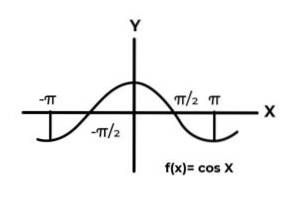
Comportamentul funcțiilor trigonometrice este similar cu cel al undelor, fiind foarte obișnuit să se găsească repetări ale variabilei dependente între imagini. De asemenea, în majoritatea cazurilor intervalul funcției este limitat la unul sau mai multe sectoare ale liniei reale.
Acesta este cazul funcțiilor sinus și cosinus. Unde valorile lor fluctuează în intervalul [-1, 1]. Acest interval trebuie să condiționeze codomainul pentru a obține surjectivitatea funcției.
F: R →[-eleven] definit de F (x) = Sen (x) Este o funcție surjectivă
F: R →[-eleven]definit de F (x) = Cos (x) Este o funcție surjectivă
Exercițiul 4
- Studiază funcția
F: [0, ∞ ) → R definit de F (x) = ± √x indicați dacă este un funcția surjectivă
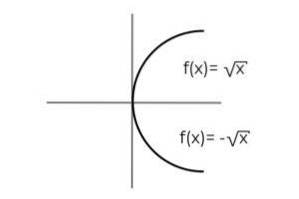
Functia F (x) = ± √x Are particularitatea că definește 2 variabile dependente de fiecare valoare a lui "x". Adică, intervalul primește 2 elemente pentru fiecare dintre cele realizate în domeniu. Trebuie verificată o valoare pozitivă și negativă pentru fiecare valoare „x”.
La observarea setului de pornire, se observă că domeniul a fost deja restricționat, pentru a evita indeterminările produse la evaluarea unui număr negativ într-o rădăcină par.
La verificarea intervalului funcției, se observă că fiecare valoare a codomainului aparține domeniului.
În acest fel se poate concluziona că:
F: [0, ∞ ) → R definit de F (x) = ± √x Este o funcție surjectivă
Exercițiul 4
- Studiază funcția F (x) = Ln x indicați dacă este un funcția surjectivă. Condiționați seturile de sosire și plecare pentru a adapta funcția la criteriile de surjectivitate.
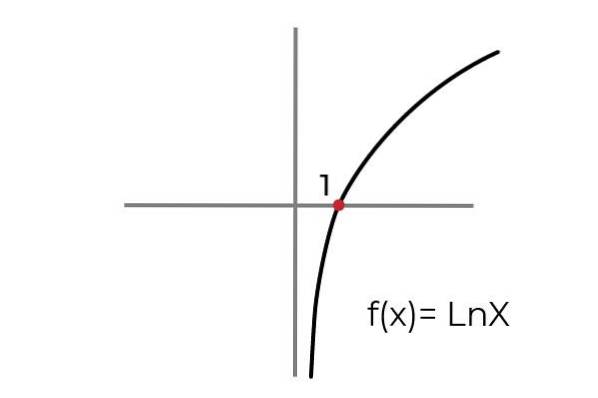
După cum se arată în grafic, funcția F (x) = Ln xeste definit pentru valori "x" mai mari decât zero. În timp ce valorile „și” sau imaginile pot lua orice valoare reală.
În acest fel putem restricționa domeniul F (x) = la interval (0 , ∞ )
Atâta timp cât gama funcției poate fi păstrată ca set de numere reale R.
Având în vedere acest lucru, se poate concluziona că:
F: [0, ∞ ) → R definit de F (x) = Ln x Este o funcție surjectivă
Exercițiul 5
- Studiați funcția de valoare absolută F (x) = | x | și desemnați seturile de sosire și plecare care îndeplinesc criteriile de surjectivitate.
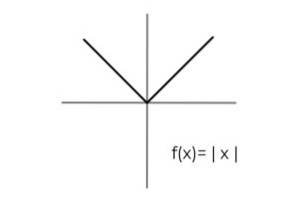
Domeniul funcției este valabil pentru toate numerele reale R. În acest fel, singura condiționare trebuie efectuată în codomain, luând în considerare faptul că funcția de valoare absolută ia numai valori pozitive..
Procedăm la stabilirea codomainului funcției care îl echivalează cu rangul aceleiași
[0 , ∞ )
Acum se poate concluziona că:
F: [0, ∞ ) → R definit de F (x) = | x | Este o funcție surjectivă
Exerciții propuse
- Verificați dacă următoarele funcții sunt surjective:
- F: (0, ∞ ) → R definit de F (x) = Jurnal (x + 1)
- F: R → R definit de F (x) = x3
- F: R →[1, ∞ ) definit de F (x) = xDouă + 1
- [0, ∞ ) → R definit de F (x) = Jurnal (2x + 3)
- F: R → R definit de F (x) = Sec x
- F: R - 0 → R definit de F (x) = 1 / x
Referințe
- Introducere în logică și gândire critică. Merrilee H. Salmon. Universitatea din Pittsburgh
- Probleme în analiza matematică. Piotr Biler, Alfred Witkowski. Universitatea din Wroclaw. Polonia.
- Elemente de analiză abstractă. Dr. Mícheál O'Searcoid. Departamentul de matematică. Colegiul universitar Dublin, Beldfield, Dublind 4
- Introducere în logică și în metodologia științelor deductive. Alfred Tarski, New York Oxford. Presa Universitatii Oxford.
- Principiile analizei matematice. Enrique Linés Escardó. Editorial Reverté S. A 1991. Barcelona Spania.


Nimeni nu a comentat acest articol încă.