Formule de inducție magnetică, modul în care este calculată și exemple

inducție magnetică sau densitatea fluxului magnetic este o alterare a mediului cauzată de prezența curenților electrici. Acestea modifică natura spațiului care le înconjoară, creând un mediu rural vector.

Vectorul inducție magnetică, densitatea fluxului magnetic Sau pur și simplu camp magnetic B, are trei caracteristici distinctive: o intensitate exprimată printr-o valoare numerică, o direcție și, de asemenea, un sens dat în fiecare punct al spațiului. Este evidențiat cu caractere aldine pentru a-l deosebi de cantități pur numerice sau scalare.

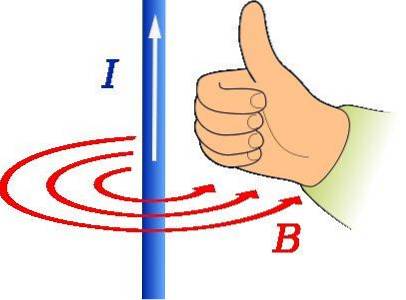
Regula degetului mare dreapta este utilizată pentru a găsi direcția și direcția câmpului magnetic cauzate de un fir de transport curent, așa cum se arată în figura de mai sus.

Degetul mare al mâinii drepte ar trebui să indice în direcția curentului. Apoi rotația celor patru degete rămase indică forma B, care în figură este reprezentată de cercurile roșii concentrice.

Într-un astfel de caz, adresa B este tangențial la circumferința concentrică cu firul și este în sens invers acelor de ceasornic.

inducție magnetică B În sistemul internațional, se măsoară Tesla (T), cu toate acestea este mai frecvent să se măsoare într-o altă unitate numită Gauss (G). Ambele unități au fost numite respectiv în onoarea lui Nikola Tesla (1856-1943) și a lui Carl Friedrich Gauss (1777-1855) pentru contribuțiile lor extraordinare la știința electricității și magnetismului..

Indice articol

• 1 Care sunt proprietățile inducției magnetice sau ale densității fluxului magnetic?
• 2 Legea lui Biot-Savart
• 3 formule
• 4 Cum se calculează?
  • 4.1 Exemplu
• 5 Referințe

Care sunt proprietățile inducției magnetice sau ale densității fluxului magnetic?

O busolă care este plasată lângă firul sub tensiune se va alinia întotdeauna cu B. Fizicianul danez Hans Christian Oersted (1777-1851) a fost primul care a observat acest fenomen la începutul secolului al XIX-lea.

Și când curentul încetează, busola indică din nou spre nord geografic, ca întotdeauna. Schimbând cu atenție poziția busolei, se obține o hartă a formei câmpului magnetic.

Această hartă este întotdeauna în formă de cercuri concentrice la fir, așa cum este descris la început. În acest fel puteți vizualiza B.

Chiar dacă firul nu este drept, vectorul B va forma cercuri concentrice în jurul său. Pentru a determina forma câmpului, imaginați-vă doar segmente foarte mici de sârmă, atât de mici încât să pară rectilinii și înconjurate de cercuri concentrice..

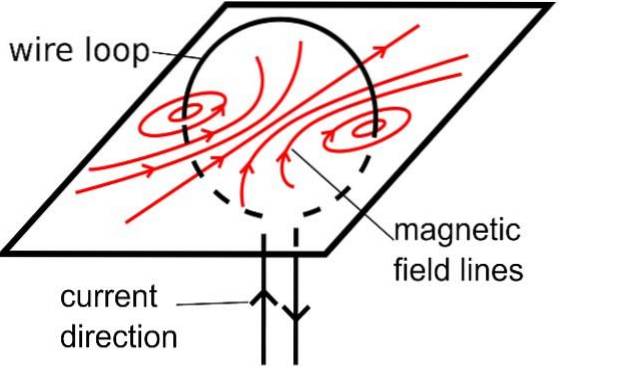
Aceasta indică o proprietate importantă a liniilor câmpului magnetic. B: nu au început sau sfârșit, sunt întotdeauna curbe închise.

Legea lui Biot-Savart

Secolul al XIX-lea a marcat începutul erei electricității și magnetismului în știință. În jurul anului 1820 fizicienii francezi Jean Marie Biot (1774-1862) și Felix Savart (1791-1841) au descoperit legea care le poartă numele și care ne permite să calculăm vectorul B.

Au făcut următoarele observații despre contribuția la câmpul magnetic produs de un segment de sârmă de lungime diferențială dl care transportă un curent electric Eu:

• Mărimea B scade odată cu pătratul invers al distanței până la fir (acest lucru are sens: departe de fir intensitatea lui B trebuie să fie mai puțin decât punctele apropiate).
• Mărimea B este proporțională cu intensitatea curentului Eu care trece prin fir.
• Adresa de B este tangențial la circumferința razei r centrat pe fir și sensul de B este dat, așa cum am spus, de regula degetului mare drept.

Produsul încrucișat sau produsul încrucișat este instrumentul matematic adecvat pentru a exprima ultimul punct. Pentru a stabili un produs vector, sunt necesari doi vectori, care sunt definiți după cum urmează:

• dl este vectorul a cărui magnitudine este lungimea segmentului diferențial dl
• r este vectorul care merge de la fir până la punctul în care doriți să găsiți câmpul

Formule

Toate acestea pot fi combinate într-o expresie matematică:

Constanta de proporționalitate necesară pentru stabilirea egalității este permeabilitatea magnetică a spațiului liber μ_sau  = 4π.10^-7 T.m / A

Această expresie este legea Biot și Savart, care ne permite să calculăm câmpul magnetic al unui segment curent.

Un astfel de segment la rândul său trebuie să facă parte dintr-un circuit mai mare și mai închis: o distribuție de curent.

Condiția ca circuitul să fie închis este necesară pentru a curge un curent electric. Curentul electric nu poate circula în circuite deschise.

În cele din urmă, pentru a găsi câmpul magnetic total al respectivei distribuții de curent, se adaugă toate contribuțiile fiecărui segment diferențial dl. Acest lucru este echivalent cu integrarea pe întreaga distribuție:

Pentru a aplica legea Biot-Savart și a calcula vectorul de inducție magnetică, este necesar să se ia în considerare câteva puncte importante foarte importante:

• Produsul încrucișat între doi vectori are ca rezultat întotdeauna un alt vector.

• 

• Este convenabil să găsiți produsul vector inainte de pentru a trece la rezoluția integralei, atunci se rezolvă integrala fiecăreia dintre componentele obținute separat.
• Este necesar să faceți o imagine a situației și să stabiliți un sistem de coordonate adecvat.
• Ori de câte ori se observă existența unei simetrii, aceasta ar trebui folosită pentru a economisi timp de calcul.
• Când există triunghiuri, teorema lui Pitagora și teorema cosinusului sunt de mare ajutor pentru stabilirea relației geometrice între variabile.

Cum se calculează?

Cu un exemplu practic de calcul al B pentru un fir drept, se recomandă aceste recomandări.

Exemplu

Calculați vectorul câmpului magnetic pe care îl produce un fir rectiliniu foarte lung într-un punct P din spațiu, conform figurii prezentate.

Din figură trebuie:

• Sârma este direcționată în direcție verticală, curentul I curgând în sus. Această direcție este + y în sistemul de coordonate, a cărui origine este în punctul O.

• 

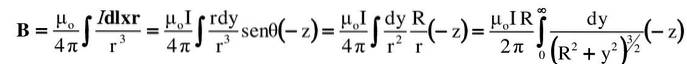
• Într-un astfel de caz, conform regulii degetului mare drept, B în punctul P este îndreptată spre interiorul hârtiei, de aceea este notată cu un cerc mic și un „x” în figură. Această adresă va fi luată ca -z.
• Triunghiul dreptunghic al cărui picioare sunt Da Da R, relaționează ambele variabile în conformitate cu teorema lui Pitagora: r^Două= R^Două+Da^Două

Toate acestea se substituie integralului. Produsul încrucișat sau cruce este indicat de mărimea sa plus direcția și sensul său:

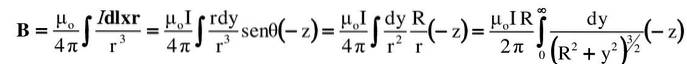
Integrala propusă se găsește într-un tabel de integrale sau este rezolvată printr-o substituție trigonometrică adecvată (cititorul poate verifica rezultatul folosind y = Rtg θ):

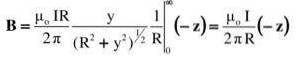
Rezultatul este de acord cu ceea ce era de așteptat: magnitudinea câmpului scade odată cu distanța R și crește proporțional cu intensitatea curentului I.

Deși un fir infinit de lung este o idealizare, expresia obținută este o foarte bună aproximare pentru câmpul unui fir lung.

Cu legea lui Biot și Savart, este posibil să se găsească câmpul magnetic al altor distribuții extrem de simetrice, cum ar fi o buclă circulară care transportă curent sau fire îndoite care combină segmente rectilinii și curvilinei..

Desigur, pentru a rezolva analitic integralul propus, problema trebuie să aibă un grad ridicat de simetrie. În caz contrar, alternativa este rezolvarea numerică a integralei.

Referințe

1. Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 2. Mexic. Editorii de învățare Cengage. 367-372.