
Formula și ecuațiile legii lui Ampère, dovada, exerciții
Legea lui Ampère afirmă că circulația vectorului de inducție magnetică B este proporțională cu intensitatea I a curentului care curge prin el.
La rândul său circulația B este suma tuturor produselor dintre componenta tangențială B║ iar lungimea unui segment mic Δℓ a unei curbe închise C, în jurul unui circuit. În termeni matematici este scris astfel:
∑ B║ .Δℓ ∝ Eu
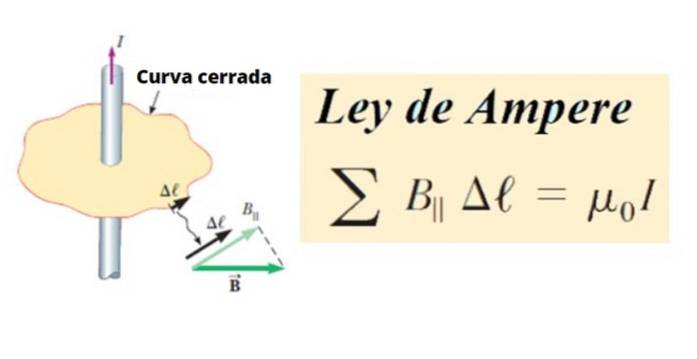
Ca o linie arbitrară sau o curbă C, poate fi împărțită în segmente mici Δℓ, iar acestea la rândul lor pot fi infinitezimale, apoi se numesc dℓ.
În acest caz, însumarea devine o linie integrală a produsului scalar dintre vectori B și ds. Acest produs conține componenta tangențială a lui B, care este B cosθ, unde θ este unghiul dintre vectori:
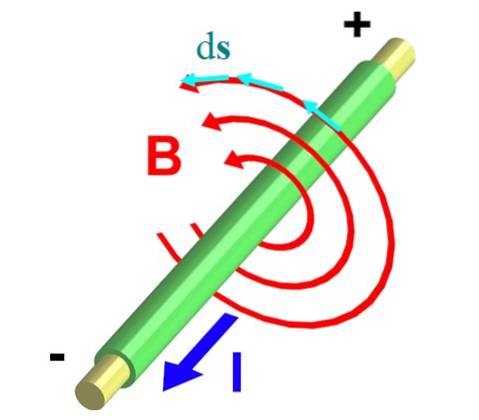
Cercul mic prin integrală înseamnă că integrarea are loc pe o cale închisă C, care în acest caz implică curentul care curge prin secțiunea transversală a conductorului.
Constanta de proporționalitate necesară pentru stabilirea egalității este μsau, permeabilitatea vidului. În acest fel, legea lui Ampère este:

Legea lui Ampère ne spune că integrala de linie ∫C B ∙ ds este exact μsauEu, dar nu ne oferă detalii despre modul în care este orientat câmpul magnetic B în ceea ce privește curba C în fiecare punct și nici despre modul de calcul al integralei. Ne spune doar că rezultatul este întotdeauna μsauEu.
Indice articol
- 1 Dovada legii lui Ampère
- 1.1 Câmpul magnetic al firului rectiliniu și infinit
- 2 exerciții rezolvate
- 2.1 - Exercițiul 1
- 2.2 - Exercițiul 2
- 3 Referințe
Demonstrarea legii lui Ampère
Legea lui Ampère este verificată experimental prin verificarea câmpului magnetic produs de un conductor rectiliniu foarte lung. Înainte de a aborda problema, trebuie să evidențiem două cazuri de interes special în ecuația anterioară:
-Primul este când B și ds sunt paralele, ceea ce înseamnă că B este tangențial la C. Atunci unghiul dintre ambii vectori este 0º, iar produsul scalar este pur și simplu produsul mărimilor B.ds.
-Al doilea apare dacă B și ds sunt perpendiculare, caz în care produsul scalar este 0, deoarece unghiul dintre vectori este de 90º, al cărui cosinus este 0.
Un alt detaliu important este alegerea curbei C pe care se evaluează circulația câmpului. Legea lui Ampère nu specifică ce poate fi, dar trebuie să implice distribuția curentă. De asemenea, nu spune în ce direcție să parcurgeți curba și există două posibilități pentru aceasta.
Soluția este de a atribui semne conform regulii degetului mare drept. Cele patru degete sunt curbate în direcția în care doriți să vă integrați, de obicei aceasta va fi aceeași cu câmpul B circula. Dacă curentul indică în direcția degetului mare drept, i se atribuie un semn + și dacă nu, un semn -.
Acest lucru se aplică atunci când există o distribuție cu mai mulți curenți, unele pot fi pozitive și altele negative. Suma algebrică a acestora este cea pe care urmează să o plasăm în legea lui Ampère, care este denumită de obicei ca curent blocat (după curba C).
Câmp magnetic infinit de sârmă rectilinie
Figura 2 prezintă un fir care transportă un curent I din plan. Regula degetului mare drept asigură acest lucru B circulă în sens invers acelor de ceasornic, descriind circumferințele așa cum arată săgețile roșii.

Să luăm una dintre ele, a cărei rază este r. Îl împărțim în segmente diferențiale mici ds, reprezentat de vectorii în albastru. Ambii vectori, B și ds, sunt paralele în fiecare punct al circumferinței și, astfel, integralul ∫C B ∙ ds Se transformă în:
∫C BDS
Acest lucru se datorează faptului că, așa cum am spus anterior, produsul dot B ∙ ds este produsul mărimilor vectorilor de către cosinusul de 0º. Știm rezultatul integral datorită legii lui Ampère, prin urmare scriem:
∫C BD = μsauEu
Deoarece magnitudinea câmpului este constantă pe întreaga traiectorie, acesta părăsește integralul:
B ∫C ds = μsauEu
Integrala ∫C ds reprezintă suma tuturor segmentelor infinitezimale care alcătuiesc circumferința razei r, echivalent cu lungimea sa, produsul razei sale cu 2π:
B.2πr = μsauEu
Și de acolo descoperim că magnitudinea lui B este:
B = μsauI / 2πr
Trebuie subliniat faptul că, chiar dacă calea selectată (sau circuit ampereian) nu era circulară, rezultatul a integralei rămâne μsauEu, totuși ∫C B ∙ ds nu ar mai fi B.2πr.
Prin urmare, utilitatea legii lui Ampère pentru a determina câmpul magnetic constă în alegerea distribuțiilor cu simetrie ridicată, astfel încât integrala să fie ușor de evaluat. Căile circulare și rectilinii îndeplinesc această cerință.
Exerciții rezolvate
- Exercitiul 1
Luați în considerare curbele a, b, c și d prezentate în Figura 3. Acestea implică trei curenți, doi părăsind planul, simbolizați printr-un punct ( . ), ale cărui intensități sunt 1 A și 5 A și un curent care intră în plan, care este notat printr-o cruce și a cărui magnitudine este de 2 A.
Găsiți curentul închis de fiecare curbă.
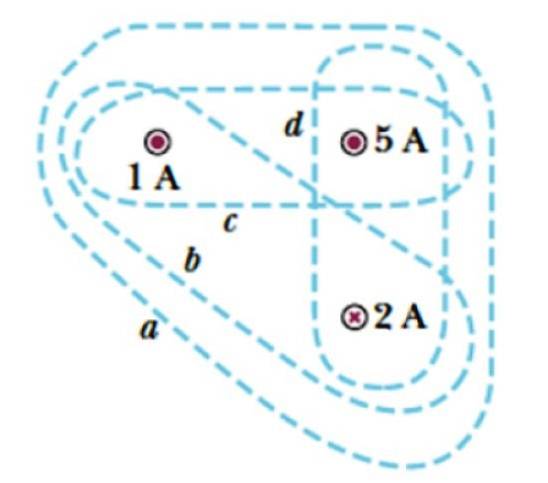
Soluţie
Curenților care ies din hârtie li se atribuie un semn +. În conformitate cu aceasta:
Curba a
Acesta cuprinde cei trei curenți, prin urmare curentul închis este + 1 A + 5 A - 2 A = 4 A.
Curba b
Numai curenții de 1 A și - 2 A se află în această curbă, prin urmare curentul închis este - 2 A.
Curba c
Acesta cuprinde curenții de ieșire 1A și 5 A, prin urmare curentul blocat este de 6 A.
Curba d
Curenții din interiorul acestuia sunt +5 A și - 2 A, deci conține un curent net de 3 A.
- Exercițiul 2
Calculați magnitudinea câmpului magnetic produs de un fir drept foarte lung, într-un punct situat la 1 metru de acesta, dacă firul transportă un curent de 1 A.
Soluţie
Conform legii lui Ampère, câmpul firului este dat de:
B = μsauI / 2πr = (4π x 10-7 x 1 / 2π x 1) T = 2 x 10-7 T.
Referințe
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 6. Electromagnetismul. Editat de Douglas Figueroa (USB).
- Knight, R. 2017. Fizica pentru oamenii de știință și inginerie: o abordare strategică. Pearson.
- Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 2.
- Serway, R. 2009. Fizica colegiului. Cengage Learning.
- Tipler, P. (2006) Fizică pentru știință și tehnologie. Ediția a 5-a Volumul 2. Editorial Reverté.



Nimeni nu a comentat acest articol încă.