Blochează elemente de algebră, exemple, exerciții rezolvate

bloc algebra se referă la setul de operații care se execută prin blocuri. Acestea și alte elemente servesc la reprezentarea schematică a unui sistem și la vizualizarea cu ușurință a răspunsului său la o intrare dată..

În general, un sistem conține diverse elemente electrice, electronice și electromecanice și fiecare dintre ele, cu funcția și poziția sa respectivă în sistem, precum și modul în care sunt legate, este conturat prin blocuri funcționale.

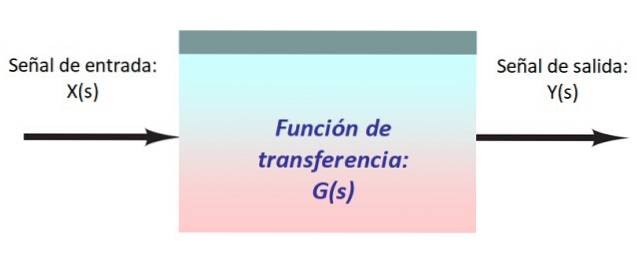
În figura de mai sus există un sistem foarte simplu, format dintr-un semnal de intrare X (s), care intră în bloc cu funcția de transfer G (s) care îl modifică și produce ieșirea Y (s).

Este convenabil să reprezentați semnalele și calea lor prin sistem prin intermediul săgeților care intră și ies din fiecare bloc. De obicei fluxul semnalului este direcționat de la stânga la dreapta.

Avantajul acestui tip de schemă este ajutorul vizual pe care îl oferă în înțelegerea sistemului, chiar dacă nu este o reprezentare fizică a sistemului. De fapt, diagrama bloc nu este unică, deoarece, în funcție de punctul de vedere, pot fi trase chiar mai multe diagrame ale aceluiași sistem..

De asemenea, se poate întâmpla ca aceeași diagramă să deservească mai multe sisteme care nu sunt neapărat legate între ele, atâta timp cât descrie în mod adecvat comportamentul lor. Există diferite sisteme al căror răspuns este similar în multe privințe, de exemplu un circuit LC (inductor-condensator) și un sistem cu arc de masă..

Indice articol

• 1 Ce este o diagramă bloc?
• 2 Elemente ale schemei bloc
  • 2.1 Semnalul
  • 2.2 Blocul
  • 2.3 Punctul sumă
  • 2.4 Punctul de ramură
• 3 Exemple de reguli de algebră bloc
  • 3.1 Blocuri în cascadă
  • 3.2 Blocuri în paralel
  • 3.3 Mutați un sumator la stânga
  • 3.4 Mutați un sumator spre dreapta
  • 3.5 Deplasarea unui punct de ramificare de la stânga la dreapta
  • 3.6 Mutați un punct de ramificare de la dreapta la stânga
  • 3.7 Sistem de feedback
  • 3.8 Sistem cu feedback și traductor
• 4 exerciții rezolvate
  • 4.1 Exercițiul 1
  • 4.2 Exercițiul 2
• 5 Referințe

Ce este o diagramă bloc?

Sistemele sunt, în general, mai complicate decât cea din Figura 1, dar algebra bloc oferă o serie de reguli simple pentru a manipula schema sistemului și a o reduce la cea mai simplă versiune..

După cum sa explicat la început, diagrama folosește blocuri, săgeți și cercuri pentru a stabili relația dintre fiecare componentă a sistemului și fluxul de semnale care trec prin el..

Algebra bloc vă permite să comparați două sau mai multe semnale prin adăugarea, scăderea și înmulțirea acestora, precum și analiza contribuției pe care fiecare componentă o aduce la sistem.

Datorită acestui fapt, este posibil să reduceți întregul sistem la un singur semnal de intrare, o singură funcție de transfer care descrie pe deplin acțiunea sistemului și ieșirea corespunzătoare..

Elemente diagramă bloc

Elementele schemei bloc sunt următoarele:

Semnalul

Semnalele sunt de o natură foarte variată, de exemplu, este obișnuit ca acesta să fie un curent electric sau o tensiune, dar poate fi lumină, sunet și multe altele. Important este că conține informații despre un anumit sistem.

Semnalul este notat cu o majusculă dacă este o funcție a variabilei s a transformatei Laplace: X (s) (vezi figura 1) sau cu litere mici dacă este o funcție a timpului t, ca x (t).

În diagrama bloc, semnalul de intrare este reprezentat de o săgeată îndreptată spre bloc, în timp ce semnalul de ieșire, notat ca Y (s) sau y (t), este indicat de o săgeată de ieșire.

Atât semnalele de intrare, cât și cele de ieșire sunt unice, iar direcția în care circulă informația este determinată de direcția săgeții. Iar algebra este aceeași pentru oricare dintre cele două variabile.

Blocul

Blocul este reprezentat de un pătrat sau un dreptunghi (a se vedea figura 1) și poate fi utilizat pentru a efectua operațiuni sau pentru a implementa funcția de transfer, care este de obicei notată cu litera mare G. Această funcție este un model matematic care descrie răspunsul oferit de sistem unui semnal de intrare.

Funcția de transfer poate fi exprimată în termeni de timp t ca G (t) sau variabilă s ca G (s).

Când semnalul de intrare X (s) ajunge la bloc, acesta este înmulțit cu funcția de transfer și transformat în semnalul de ieșire Y (s). Matematic se exprimă astfel:

Y (s) = X (s) .G (s)

În mod echivalent, funcția de transfer este raportul dintre transformata Laplace a semnalului de ieșire și transformata Laplace a semnalului de intrare, cu condiția ca condițiile inițiale ale sistemului să fie nule:

G (s) = Y (s) / X (s)

Suma punctului

Punctul de adunare sau adder este simbolizat printr-un cerc cu o cruce în interior. Se utilizează pentru a combina, prin adunare și scădere, două sau mai multe semnale. La sfârșitul săgeții care simbolizează semnul, un semn + este plasat direct dacă semnul respectiv este adăugat sau un semn - dacă este scăzut..

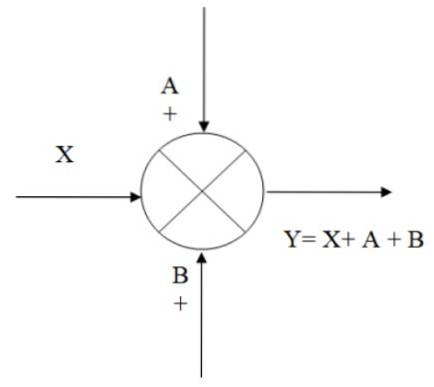
În figura următoare există un exemplu de funcționare a sumatorului: avem semnalul de intrare X, la care se adaugă semnalele A și B, obținând ca rezultat ieșirea Y, care este echivalentă algebric cu:

Y = X + A + B

Punct de ramură

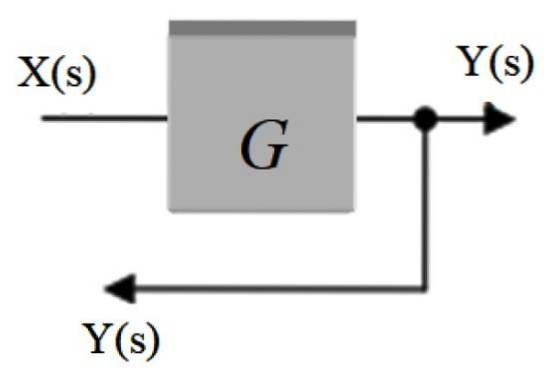
Se mai numește punct de bifurcație. În el, semnalul care iese dintr-un bloc este distribuit către alte blocuri sau către un sumator. Este reprezentat de un punct plasat pe săgeata semnalului și din ea iese o altă săgeată care redirecționează semnalul către o altă parte.

Exemple de reguli de algebră bloc

Așa cum s-a explicat anterior, ideea este să exprimăm sistemul folosind diagrama bloc și să-l reducem pentru a găsi funcția de transfer care îl descrie. Următoarele sunt regulile de algebră bloc pentru a simplifica diagramele:

Blocuri în cascadă

Când ai un semnal care trece succesiv prin blocurile G.₁, G_Două, G₃..., este redus la un singur bloc a cărui funcție de transfer este produsul lui G₁, G_Două, G₃...

În exemplul următor, semnalul X (s) intră în primul bloc și ieșirea acestuia este:

Da₁(s) = X (s) .G₁(s)

Rotiți Y₁(s) introduceți blocul G_Două(s), a căror ieșire este:

Da_Două(s) = X (s) .G₁(s). G_Două(s)

Procedura este valabilă pentru n blocuri în cascadă:

Da_n (s) = X (s). G₁(s) .G_Două(s) ... G_n(s)

Blocuri paralele

În diagrama din stânga, semnalul X (s) se ramifică pentru a intra în blocurile G.₁(s) și G_Două(s):

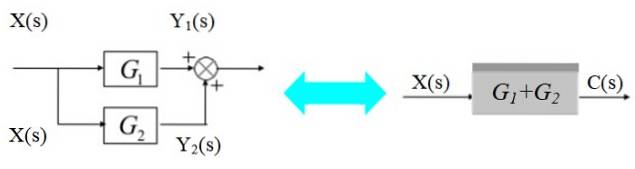
Semnalele de ieșire respective sunt:

Da₁(s) = X (s) .G₁(s)

Da_Două(s) = X (s) .G_Două(s)

Aceste semnale sunt adăugate pentru a obține:

C (s) = Y₁(s) + Y_Două(s) = X (s). [G₁(s) + G_Două(s)]

Așa cum se arată în diagrama din dreapta.

Mutați un adăugător spre stânga

Un sumator poate fi mutat în stânga blocului după cum urmează:

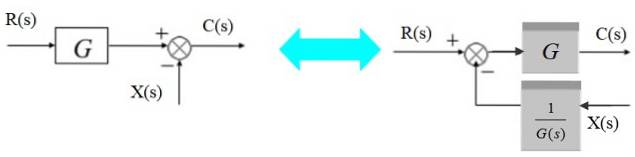
În stânga semnalul de ieșire este:

C (s) = R (s). G (s) - X (s)

Echivalent cu dreapta:

C (s) = [R (s) - X (s) / G (s)]. G (s)

Mutați un adăugător spre dreapta

Adderul poate fi mutat în dreapta blocului astfel:

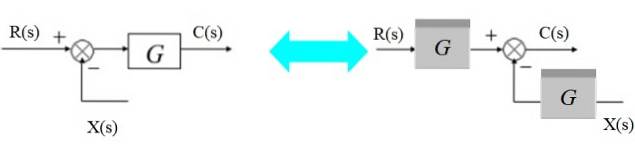
În stânga avem: [R (s) - X (s)]. G (s) = C (s)

Și în dreapta:

R (s). G (s) - X (s). G (s) = C (s)

Mutați un punct de ramificare de la stânga la dreapta

Pentru a muta punctul de ramificare de la stânga la dreapta blocului, observați doar că ieșirea C (s) la dreapta este produsul X (s) .G (s). Deoarece doriți să îl convertiți din nou în X (s), înmulțiți cu inversul lui G (s).

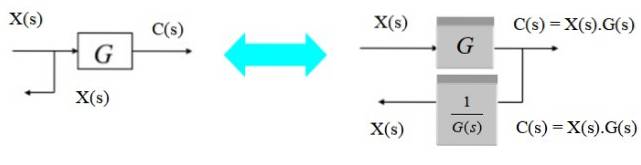
Mutați un punct de ramificare de la dreapta la stânga

Alternativ, punctul de ramificare poate fi deplasat de la dreapta la stânga după cum urmează:

Deoarece la ieșirea din ramură dorim să obținem C (s), pur și simplu introduceți un nou bloc G (s) într-un punct de ramificare din stânga blocului original.

Sistem de feedback

În sistemul de mai jos, semnalul de ieșire C (s) este readus prin sumatorul din stânga:

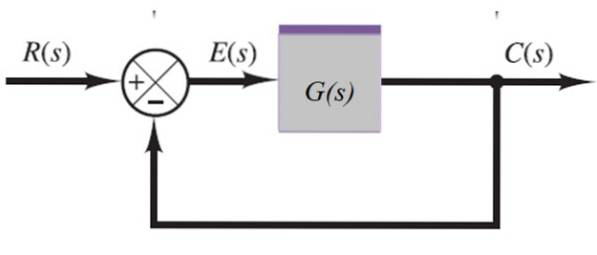
C (s) = E (s) .G (s)

Dar:

E (s) = R (s) -C (s)

Înlocuind această expresie în ecuația anterioară rămâne: C (s) = [R (s) -C (s)]. G (s), din care se pot rezolva C (s):

C (s) + C (s) .G (s) = R (s) .G (s) → C (s). [1 + G (s)] = R (s) .G (s)

C (s) = R (s). G (s) / [1 + G (s)]

Sau alternativ:

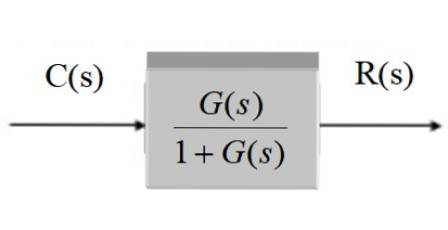
C (s) / R (s) = G (s) / [1 + G (s)]

În formă grafică, după simplificare rămâne:

Sistem cu feedback și traductor

Traductorul constă din funcția de transfer H (s):

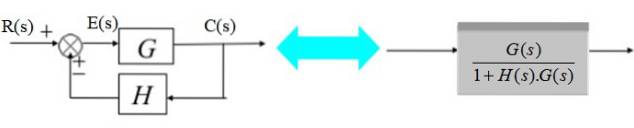
În diagrama din dreapta, semnalul de ieșire C (s) este:

C (s) = E (s). G (s) cu E (s) = R (s) - C (s). H (s)

Atunci:

C (s) = [R (s) - C (s). H (s)]. G (s)

C (s) [1+ H (s) .G (s)] = R (s) .G (s)

Prin urmare, C (s) pot fi rezolvate prin:

C (s) = G (s) .R (s) / [1+ H (s) .G (s)]

Iar funcția de transfer va fi:

G (s) / [1+ H (s) .G (s)]

Așa cum se arată în diagrama simplificată din dreapta.

Exerciții rezolvate

Exercitiul 1

Găsiți funcția de transfer a următorului sistem:

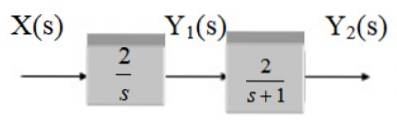
Soluţie

Tratează două blocuri în cascadă, prin urmare funcția de transfer este produsul funcțiilor G₁ și G_Două.

Trebuie sa:

G₁ = 2 / s

G_Două = 2 / (s + 1)

Prin urmare, funcția de transfer căutată este:

G (s) = 4 / [s (s + 1)]

Exercițiul 2

Reduceți următorul sistem:

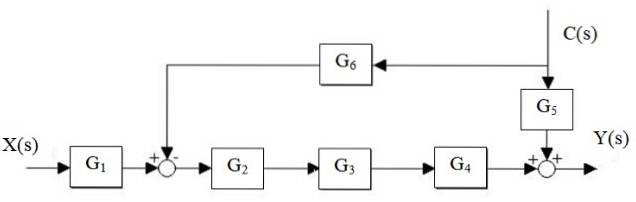
Soluţie

Mai întâi cascada G este redusă_Două, G₃ și G_4, iar paralela G este separată₅ și G₆:

Apoi, sumatorul din stânga blocului G_Două ⋅G₃ ⋅ G₄ se deplasează spre dreapta:

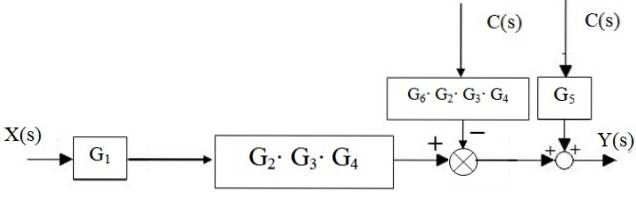
Sumatoarele din dreapta sunt reduse la doar unul, precum și blocurile în cascadă:

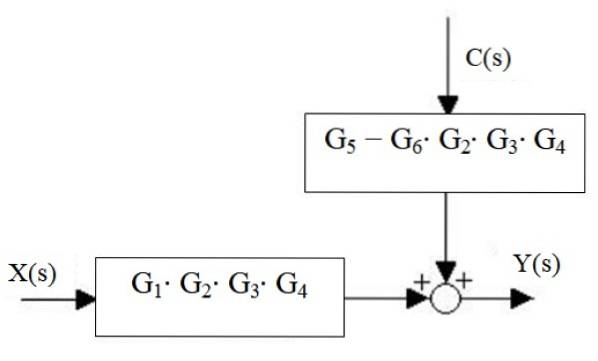
În cele din urmă, ieșirea sistemului este:

Y (s) = X (s) ⋅G₁⋅ G_Două ⋅G₃ ⋅ G₄ + C (s) ⋅ [G₅ - G₆ ⋅ G_Două ⋅G₃ ⋅ G₄]

Referințe

1. Alaydi, J. Schema bloc a sistemului de control. Recuperat de pe: site.iugaza.edu.ps.
2. Bolton, W. 2006. Ingineria controlului. Al 2-lea. Ediție. Alfa Omega.
3. Cwalinsky, J. Introducere în algebra blocului de sistem. Recuperat de pe: cedengineering.com.
4. Dademuchconnection. Diagrama blocurilor. Recuperat de pe: dademuch.com.
5. Ogata, K. 2010. Inginerie modernă de control. Al 5-lea. Ediție. Pearson.