
Fundamentele, magnitudinile, vectorii algebrei vectoriale
algebra vectorială este o ramură a matematicii însărcinată cu studierea sistemelor de ecuații liniare, vectori, matrici, spații vectoriale și transformările lor liniare. Este legat de domenii precum ingineria, rezoluția ecuațiilor diferențiale, analiza funcțională, cercetarea operațiunilor, grafica computerizată, printre altele..
O altă zonă pe care a adoptat-o algebra liniară este fizica, deoarece prin aceasta a fost posibil să se dezvolte studiul fenomenelor fizice, descriindu-le prin utilizarea vectorilor. Acest lucru a făcut posibilă o mai bună înțelegere a universului.

Indice articol
- 1 Noțiuni fundamentale
- 1.1 Geometric
- 1.2 Analitic
- 1.3 Axiomatic
- 2 magnitudini
- 2.1 Mărimea scalară
- 2.2 Magnitudine vectorială
- 3 Ce sunt vectori?
- 3.1 Modul
- 3.2 Adresă
- 3.3 Simțul
- 4 Clasificarea vectorilor
- 4.1 Vector fix
- 4.2 Vector gratuit
- 4.3 Vector glisant
- 5 Proprietățile vectorilor
- 5.1 vectori ai obiectivelor echipei
- 5.2 Vectorii echivalenți
- 5.3 Egalitatea vectorilor
- 5.4 Vectorii opuși
- 5.5 Vectorul unitar
- 5.6 Vector nul
- 6 Componente ale unui vector
- 6.1 Exemple
- 7 Operații cu vectori
- 7.1 Adunarea și scăderea vectorilor
- 7.2 Înmulțirea vectorilor
- 8 Referințe
Fundamente
Algebra vectorială a luat naștere din studiul cuaternionilor (extensia numerelor reale) 1, i, j și k, precum și din geometria carteziană promovată de Gibbs și Heaviside, care au realizat că vectorii ar servi ca instrument pentru a reprezenta diverse fenomene fizice.
Algebra vectorială este studiată prin trei elemente fundamentale:
Geometric
Vectorii sunt reprezentați prin linii care au o orientare, iar operații precum adunarea, scăderea și înmulțirea cu numere reale sunt definite prin metode geometrice..
Analitic
Descrierea vectorilor și a operațiunilor lor se face cu numere, numite componente. Acest tip de descriere este rezultatul unei reprezentări geometrice, deoarece se utilizează un sistem de coordonate.
Axiomatic
Se face o descriere a vectorilor, indiferent de sistemul de coordonate sau de orice tip de reprezentare geometrică.
Studiul figurilor în spațiu se face prin reprezentarea lor într-un sistem de referință, care poate fi într-una sau mai multe dimensiuni. Printre sistemele principale se numără:
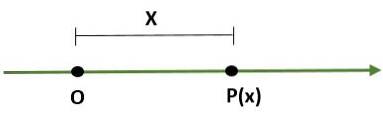
- Sistem unidimensional, care este o linie în care un punct (O) reprezintă originea și un alt punct (P) determină scala (lungimea) și direcția sa:
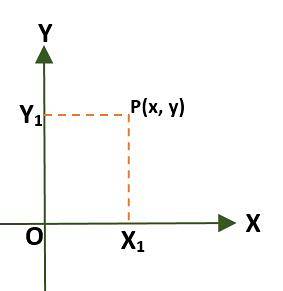
- Sistem de coordonate dreptunghiulare (bidimensional), care este alcătuit din două linii perpendiculare numite axa x și axa y, care trec printr-o origine punct (O); în acest fel planul este împărțit în patru regiuni numite cadrane. În acest caz, un punct (P) din plan este dat de distanțele care există între axe și P.
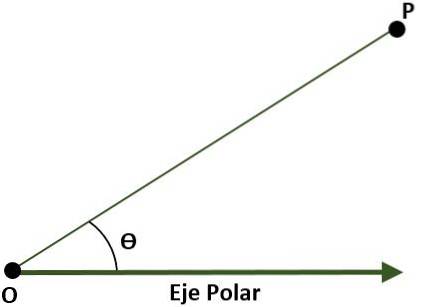
- Sistem de coordonate polare (bidimensional). În acest caz, sistemul este compus dintr-un punct O (origine) care se numește pol și o rază cu origine în O numită axă polară. În acest caz, punctul P al planului, cu referire la pol și la axa polară, este dat de unghiul (Ɵ), care este format de distanța dintre origine și punctul P.
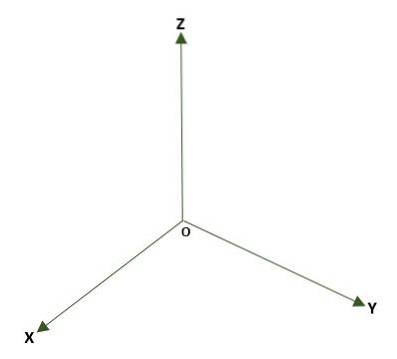
- Sistem tridimensional dreptunghiular, format din trei linii perpendiculare (x, y, z) a căror origine este un punct O în spațiu. Se formează trei planuri de coordonate: xy, xz și yz; spațiul va fi împărțit în opt regiuni numite octanți. Referința unui punct P în spațiu este dată de distanțele care există între planuri și P.
Mărimi
O magnitudine este o mărime fizică care poate fi numărată sau măsurată printr-o valoare numerică, ca în cazul unor fenomene fizice; cu toate acestea, este adesea necesar să puteți descrie aceste fenomene cu alți factori decât numerici. De aceea mărimile sunt clasificate în două tipuri:
Magnitudine scalară
Sunt acele cantități care sunt definite și reprezentate numeric; adică printr-un modul împreună cu o unitate de măsură. De exemplu:
a) Timp: 5 secunde.
b) Masa: 10 kg.
c) Volum: 40 ml.
d) Temperatura: 40 ºC.
Magnitudine vectorială
Sunt acele cantități care sunt definite și reprezentate de un modul împreună cu o unitate, precum și de un sens și direcție. De exemplu:
a) Viteza: (5ȋ - 3ĵ) m / s.
b) Accelerare: 13 m / sDouă; S 45º E.
c) Forța: 280 N, 120º.
d) Greutate: -40 ĵ kg-f.
Mărimile vectoriale sunt reprezentate grafic prin vectori.
Ce sunt vectori?
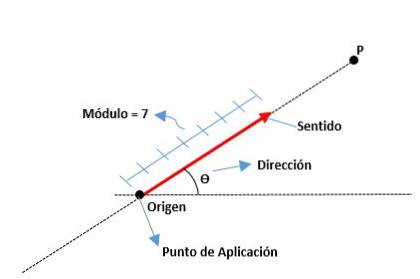
Vectorii sunt reprezentări grafice ale unei mărimi vectoriale; adică sunt segmente de linie în care capătul lor final este vârful unei săgeți.
Acestea sunt determinate de lungimea modulului sau segmentului, direcția sa, care este indicată de vârful săgeții sale și direcția sa în funcție de linia căreia îi aparține. Originea unui vector este cunoscută și sub numele de punct de aplicare.
Elementele unui vector sunt următoarele:
Modul
Este distanța de la origine la sfârșitul unui vector, reprezentată printr-un număr real împreună cu o unitate. De exemplu:
| OM | = | A | = A = 6 cm
Direcţie
Este măsura unghiului care există între axa x (de la pozitiv) și vector, precum și punctele cardinale (nord, sud, est și vest) sunt utilizate.
Sens
Este dat de vârful săgeții situat la capătul vectorului, indicând către ce se îndreaptă.
Clasificarea vectorilor
În general, vectorii sunt clasificați ca:
Vector fix
Este unul al cărui punct de aplicare (origine) este fix; adică rămâne legat de un punct din spațiu, deci nu se poate mișca în acest.
Vector gratuit
Se poate deplasa liber în spațiu, deoarece originea sa se mută în orice punct fără a-și schimba modulul, direcția sau direcția..
Vector glisor
Este unul care își poate transfera originea de-a lungul liniei sale de acțiune fără a-și schimba modulul, direcția sau direcția..
Proprietățile vectorilor
Printre principalele proprietăți ale vectorilor se numără următoarele:
Lentile de echipă Vectors
Sunt acei vectori liberi care au același modul, direcție (sau sunt paraleli) și sens ca un vector glisant sau un vector fix.
Vectorii echivalenți
Apare atunci când doi vectori au aceeași direcție (sau sunt paraleli), același sens și, în ciuda faptului că au module și puncte de aplicație diferite, provoacă aceleași efecte.
Egalitatea vectorială
Acestea au același modul, direcție și sens, chiar și atunci când punctele lor de plecare sunt diferite, ceea ce permite unui vector paralel să se traducă fără a-l afecta..
Vectori opuși
Sunt cei care au același modul și direcție, dar simțul lor este opus.
Vector unitate
Este unul în care modulul este egal cu unitatea (1). Acest lucru se obține prin împărțirea vectorului la modulul său și este utilizat pentru a determina direcția și sensul unui vector, fie în plan, fie în spațiu, folosind vectorii de bază sau unități normalizate, care sunt:
Vector nul
Este cel al cărui modul este egal cu 0; adică punctul său de origine și sfârșitul coincid în același punct.
Componentele unui vector
Componentele unui vector sunt acele valori ale proiecțiilor vectorului pe axele sistemului de referință; În funcție de descompunerea vectorului, care poate fi pe axe bidimensionale sau tridimensionale, se vor obține două sau trei componente, respectiv..
Componentele unui vector sunt numere reale, care pot fi pozitive, negative sau chiar zero (0).
Astfel, dacă avem un vector Ā, cu originea într-un sistem dreptunghiular de coordonate în planul xy (bidimensional), proiecția pe axa x este Āx și proiecția pe axa y este Āy. Astfel, vectorul va fi exprimat ca suma vectorilor săi componenți.
Exemple
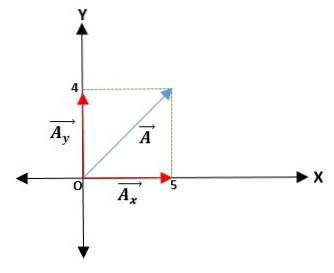
Primul exemplu
Avem un vector Ā care începe de la origine și se dau coordonatele capetelor sale. Astfel, vectorul Ā = (ĀX; LADa) = (4; 5) cm.
Dacă vectorul Ā acționează la originea unui sistem tridimensional de coordonate triunghiulare (în spațiu) x, y, z, către un alt punct (P), proiecțiile pe axele sale vor fi Āx, Āy și Āz; astfel, vectorul va fi exprimat ca suma celor trei vectori componenți ai săi.
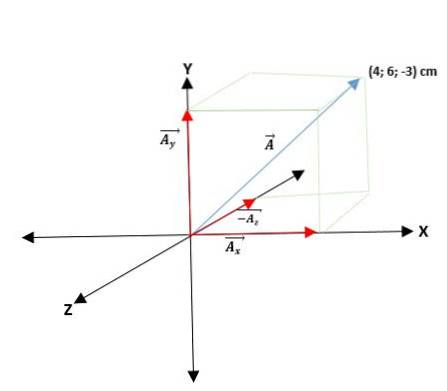
Al doilea exemplu
Avem un vector Ā care începe de la origine și se dau coordonatele capetelor sale. Astfel, vectorul Ā = (AX; LAY; LAz) = (4; 6; -3) cm.
Vectorii care au coordonatele lor dreptunghiulare pot fi exprimate în termeni de vectori de bază. Pentru aceasta, trebuie doar să multiplicați fiecare coordonată cu vectorul său de unitate respectiv, astfel încât pentru plan și spațiu să fie următoarele:
Pentru avion: Ā = AXi + ADaj.
Pentru spațiu: Ā = AXi + ADaj + Azk.
Operații vectoriale
Există multe cantități care au un modul, sens și direcție, cum ar fi accelerația, viteza, deplasarea, forța, printre altele..
Acestea sunt aplicate în diferite domenii ale științei, iar pentru a le aplica este necesar, în unele cazuri, să se efectueze operații precum adunarea, scăderea, multiplicarea și divizarea vectorilor și scalarilor..
adunarea și scăderea vectorilor
Adunarea și scăderea vectorilor este considerată o singură operație algebrică deoarece scăderea poate fi scrisă ca o sumă; de exemplu, scăderea vectorilor Ā și Ē poate fi exprimată ca:
Ā - Ē = Ā + (-Ē)
Există diferite metode pentru a efectua adunarea și scăderea vectorilor: pot fi grafice sau analitice.
Metode grafice
Folosit atunci când un vector are un modul, sens și direcție. Pentru aceasta, sunt trasate linii care formează o figură care ulterior ajută la determinarea rezultatului. Printre cele mai cunoscute sunt următoarele:
Metoda paralelogramelor
Pentru a face adunarea sau scăderea a doi vectori, se alege un punct comun pe axa coordonatelor - care va reprezenta punctul de origine al vectorilor -, păstrându-i modulul, direcția și direcția..
Liniile sunt apoi trasate paralel cu vectorii pentru a forma un paralelogram. Vectorul rezultat este diagonala care merge de la punctul de origine al ambilor vectori la vârful paralelogramului:
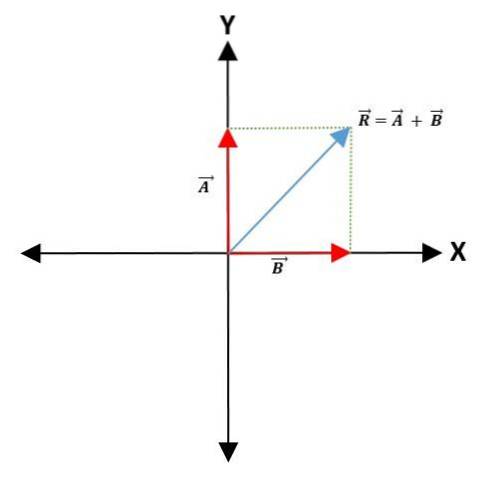
Metoda triunghiului
În această metodă vectorii sunt așezați unul după altul, păstrându-și modulele, direcțiile și direcțiile. Vectorul rezultat va fi uniunea originii primului vector cu sfârșitul celui de-al doilea vector:
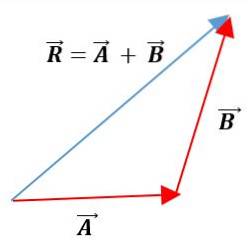
metode de analiză
Se pot adăuga sau scădea doi sau mai mulți vectori printr-o metodă geometrică sau vectorială:
Metoda geometrică
Când doi vectori formează un triunghi sau paralelogram, modulul și direcția vectorului rezultat pot fi determinate folosind legile sinusului și cosinusului. Astfel, modulul vectorului rezultat, aplicând legea cosinusului și prin metoda triunghiului, este dat de:
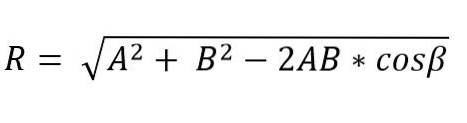
În această formulă β este unghiul opus laturii R și acesta este egal cu 180º - Ɵ.
În schimb, prin metoda paralelogramului, modulul vectorului rezultat este:
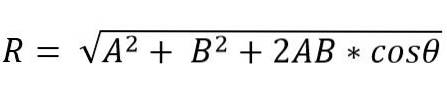
Direcția vectorului rezultat este dată de unghiul (α), care formează rezultatul cu unul dintre vectori.
Prin legea sinusului, adunarea sau scăderea vectorilor se poate face și prin metoda triunghiului sau paralelogramului, știind că în fiecare triunghi laturile sunt proporționale cu sinusurile unghiurilor:
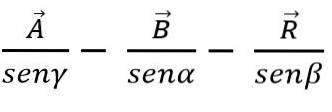
Metoda vectorială
Acest lucru se poate face în două moduri: în funcție de coordonatele sale dreptunghiulare sau de vectorii de bază.
Se poate face prin translatarea vectorilor de adăugat sau scăzut către originea coordonatelor și apoi a tuturor proiecțiilor pe fiecare dintre axe pentru plan (x, y) sau spațiu (x și Z); în final, componentele sale sunt adăugate algebric. Deci, pentru avion este:
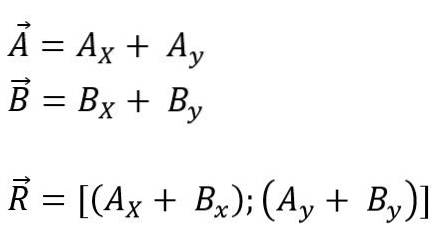
Modulul vectorului rezultat este:
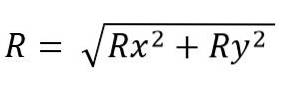
În timp ce pentru spațiu este:
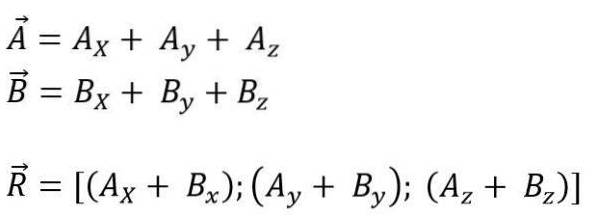
Modulul vectorului rezultat este:
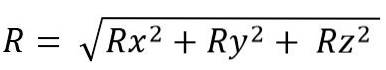
Când se efectuează sume vectoriale, se aplică mai multe proprietăți, care sunt:
- Proprietate asociativă: rezultatul nu se schimbă atunci când se adaugă mai întâi doi vectori și apoi se adaugă un al treilea vector.
- Proprietate comutativă: ordinea vectorilor nu modifică rezultatul.
- Proprietate distributivă vectorială: dacă un scalar este înmulțit cu suma a doi vectori, este egal cu înmulțirea scalarului cu fiecare vector.
- Proprietate distributivă scalară: dacă un vector este înmulțit cu suma a doi scalari, este egal cu înmulțirea vectorului pentru fiecare scalar.
Înmulțirea vectorilor
Înmulțirea sau produsul vectorilor s-ar putea face ca adunare sau scădere, dar făcând-o astfel pierde sensul fizic și nu se găsește aproape niciodată în aplicații. Prin urmare, în general, cele mai utilizate tipuri de produse sunt produsul scalar și vector.
Produs scalar
Este, de asemenea, cunoscut ca produsul punct al a doi vectori. Când modulele a doi vectori sunt înmulțite cu cosinusul celui mai mic unghi format între ele, se obține un scalar. Pentru a exprima un produs scalar între doi vectori, un punct este plasat între ei și acest lucru poate fi definit ca:
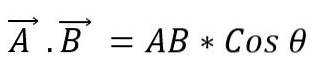
Valoarea unghiului care există între cei doi vectori va depinde dacă acestea sunt paralele sau perpendiculare; astfel, trebuie să:
- Dacă vectorii sunt paraleli și au același sens, cosinusul 0º = 1.
- Dacă vectorii sunt paraleli și au direcții opuse, cosinusul 180º = -1.
- Dacă vectorii sunt perpendiculari, cosinusul 90º = 0.
Acest unghi poate fi calculat și știind că:

Produsul dot are următoarele proprietăți:
- Proprietate comutativă: ordinea vectorilor nu modifică scalarul.
-Proprietate distributivă: dacă un scalar este înmulțit cu suma a doi vectori, este egal cu înmulțirea scalarului cu fiecare vector.
Produs vector
Înmulțirea vectorilor sau produsul încrucișat al a doi vectori A și B va avea ca rezultat un nou vector C și se exprimă folosind o cruce între vectori:
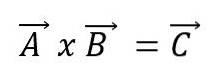
Noul vector va avea propriile sale caracteristici. În acest fel:
- Direcția: acest nou vector va fi perpendicular pe plan, care este determinat de vectorii originali.
- Direcția: aceasta se determină cu regula mâinii drepte, unde vectorul A este rotit spre B, indicând direcția de rotație cu degetele, iar direcția vectorului este marcată cu degetul mare.
- Modulul: este determinat de înmulțirea modulelor vectorilor AxB, de sinusul celui mai mic unghi care există între acești vectori. Se exprimă:
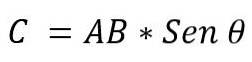
Valoarea unghiului care există între cei doi vectori va depinde dacă acestea sunt paralele sau perpendiculare. Deci, este posibil să se afirme următoarele:
- Dacă vectorii sunt paraleli și au același sens, sinusul 0º = 0.
- Dacă vectorii sunt paraleli și au direcții opuse, sinusul 180º = 0.
- Dacă vectorii sunt perpendiculari, sinusul 90º = 1.
Când un produs vector este exprimat în funcție de vectorii de bază ai acestuia, avem:
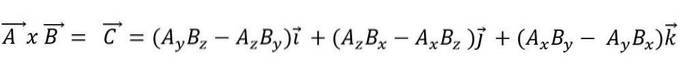
Produsul dot are următoarele proprietăți:
- Nu este comutativ: ordinea vectorilor modifică scalarul.
- Proprietate distributivă: dacă un scalar este înmulțit cu suma a doi vectori, este egal cu înmulțirea scalarului cu fiecare vector.
Referințe
- Altman Naomi, M. K. (2015). „Regresie liniară simplă”. Metode ale naturii .
- Angel, A. R. (2007). Algebra elementară. Pearson Education,.
- Arthur Goodman, L. H. (1996). Algebră și trigonometrie cu geometrie analitică. Pearson Education.
- Gusiatnikov, P. și Reznichenko, S. (s.f.). Vector Algebra în exemple. Moscova: Mir.
- Lay, D.C. (2007). Algebra liniară și aplicațiile sale. Pearson Education.
- Llinares, J. F. (2009). Algebră liniară: spațiu vectorial. Spațiu vectorial euclidian. Universitatea din Alicante.
- Mora, J. F. (2014). Algebră liniară. Tara natala.



Nimeni nu a comentat acest articol încă.