A magnitudine vectorială este orice expresie reprezentată de un vector care are o valoare numerică (modul), direcție, direcție și punct de aplicare. Câteva exemple de mărimi vectoriale sunt deplasarea, viteza, forța și câmpul electric.
Reprezentarea grafică a unei mărimi vectoriale constă dintr-o săgeată al cărei vârf indică direcția și direcția sa, lungimea sa este modulul și punctul de plecare este originea sau punctul de aplicare..
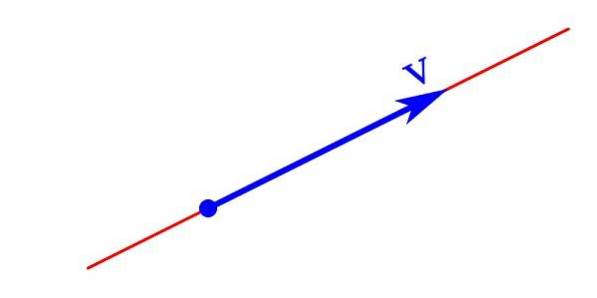
Mărimea vectorului este reprezentată analitic printr-o literă cu o săgeată în partea de sus, îndreptată spre dreapta într-o direcție orizontală. Poate fi reprezentat și printr-o scrisoare scrisă cu caractere aldine V al cărui modul ǀVǀ este scris cu caractere italice V.
Una dintre aplicațiile conceptului de mărime vectorială este în proiectarea autostrăzilor și a drumurilor, în special în proiectarea curburilor acestora. O altă aplicație este calcularea deplasării între două locuri sau schimbarea vitezei unui vehicul.
Indice articol
O cantitate vectorială este orice entitate reprezentată de un segment de linie, orientat în spațiu, care are caracteristicile unui vector. Aceste caracteristici sunt:
Modul: Este valoarea numerică care indică dimensiunea sau intensitatea mărimii vectorului.
Direcţie: Este orientarea segmentului de linie din spațiul care îl conține. Vectorul poate avea o direcție orizontală, verticală sau înclinată; nord, sud, est sau vest; nord-est, sud-est, sud-vest sau nord-vest.
Sens: Indicat de vârful săgeții la sfârșitul vectorului.
Punct de aplicare: Este originea sau punctul inițial de acționare al vectorului.
Vectorii sunt clasificați ca coliniari, paraleli, perpendiculari, concurenți, coplanari, liberi, alunecați, opuși, cu lentile în echipă, fix și unitar..
Coliniar: Aparțin sau acționează pe aceeași linie dreaptă, sunt numite și liniar dependent și poate fi verticală, orizontală și înclinată.
Paralel: Au aceeași direcție sau înclinație.
Perpendicular: doi vectori sunt perpendiculari între ei când unghiul dintre ei este de 90 °.
Concurente: Sunt vectori care atunci când alunecă de-a lungul liniei lor de acțiune coincid în același punct al spațiului.
Coplanari: Acționează pe un plan, de exemplu avionul X y.
Gratuit: Se mișcă în orice punct al spațiului, păstrându-și modulul, direcția și simțul.
Glisoare: Se deplasează de-a lungul liniei de acțiune determinată de direcția lor.
Opusuri: Au același modul și direcție, și direcția opusă.
Lentile de echipă: Au același modul, direcție și simț.
Fix: Au punctul de aplicare invariabil.
Unitar: Vectori al căror modul este unitatea.
O cantitate vectorială în spațiul tridimensional este reprezentată într-un sistem de trei axe reciproc perpendiculare (X și Z) numit triedru ortogonal.
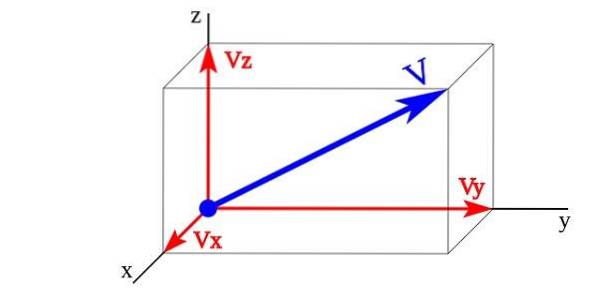
În imagine vectorii Vx, Vy, Vz sunt componentele vectoriale ale vectorului V ale căror vectori unitari sunt X,Da,z. Mărimea vectorului V este reprezentat de suma componentelor sale vectoriale.
V = Vx + Vy + Vz
Rezultatul mai multor mărimi vectoriale este suma vectorială a tuturor vectorilor și înlocuiește acești vectori într-un sistem.
Câmpul vector este regiunea spațiului în care o magnitudine vectorială corespunde fiecăruia dintre punctele sale. Dacă mărimea care se manifestă este o forță care acționează asupra unui corp sau a unui sistem fizic, atunci câmpul vector este un câmp de forțe.
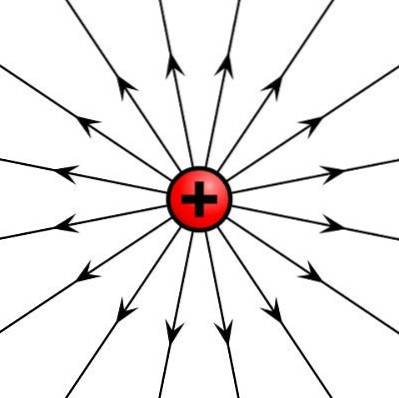
Câmpul vector este reprezentat grafic prin linii de câmp care sunt linii tangente cu magnitudinea vectorului în toate punctele din regiune. Câteva exemple de câmpuri vectoriale sunt câmpul electric creat de o sarcină electrică punctuală în spațiu și câmpul de viteză al unui fluid.
Adăugarea de vectori: Este rezultatul a doi sau mai mulți vectori. Dacă avem doi vectori SAU Da P suma este SAU + P = Q. Vectorul Î este vectorul rezultat care se obține grafic prin traducerea originii vectorului LA până la sfârșitul vectorului B.
Scădere vectorială: Scăderea a doi vectori O și P este SAU - P = Î. Vectorul Î se obține prin adăugarea la vector SAU e opusul -P. Metoda grafică este aceeași cu suma cu diferența că vectorul opus este transferat la extrem.
Produs scalar: Produsul unei cantități scalare la cu o magnitudine vectorială P este un vector mP care are aceeași direcție a vectorului P. Dacă magnitudinea scalară este zero, produsul scalar este un vector zero.
Poziția unui obiect sau a unei particule față de un sistem de referință este un vector dat de coordonatele sale dreptunghiulare X și Z, și este reprezentat de componentele sale vectoriale xî, andĵ, zk. Vectori î, ĵ, k sunt vectori unitari.
O particulă într-un punct (X și Z) are un vector de poziție r = xî + andĵ + zk. Valoarea numerică a vectorului de poziție este r= √ (XDouă + DaDouă + zDouă). Schimbarea poziției particulei de la o poziție la alta față de un cadru de referință este vectorul Deplasarea Δr și se calculează cu următoarea expresie vectorială:
Δr = rDouă - r1
Accelerația medie (lam) este definit ca modificarea vitezei v într-un interval de timp Δt iar expresia de calculat este lam= Δv / Δt, fiind Δv vectorul de schimbare a vitezei.
Accelerare instantanee (la) este limita accelerației medii lam cand Δt devine atât de mic încât tinde spre zero. Accelerația instantanee este exprimată în funcție de componentele sale vectoriale
la =laXî +laDa ĵ+ lazk
Forța de atracție gravitațională exercitată de o masă M, situat la origine, pe o altă masă m într-un punct din spațiu X, Da, z este un câmp vectorial numit câmpul forței gravitaționale. Această forță este dată de expresia:
F= (- mMG /r)ȓ
r = xî + andĵ + zk
F = este magnitudinea fizică a forței gravitaționale
G = este constanta de gravitație universală
ȓ = este vectorul de poziție al masei m
Nimeni nu a comentat acest articol încă.