
Măsuri de poziție, tendință centrală și dispersie
măsuri de tendință centrală, dispersie și poziție, sunt valori care sunt utilizate pentru a interpreta corect un set de date statistice. Acestea pot fi lucrate direct, deoarece sunt obținute din studiul statistic, sau pot fi organizate în grupuri de frecvență egală, facilitând analiza..
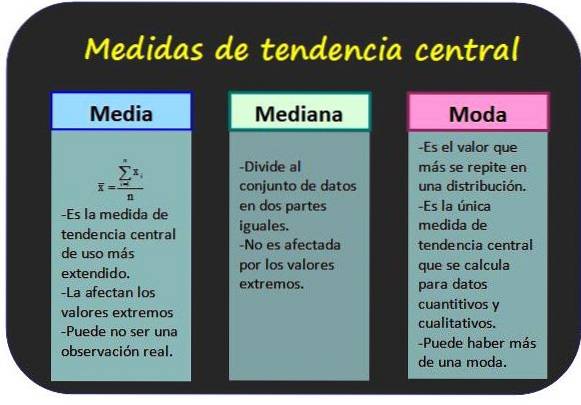
Măsuri de tendință centrală
Acestea permit cunoașterea valorilor în care sunt grupate datele statistice.
Media aritmetică
Este cunoscută și ca media valorilor unei variabile și se obține prin adăugarea tuturor valorilor și împărțirea rezultatului la numărul total de date.
-
Media aritmetică pentru datele negroupate
Fie o variabilă x din care avem n date fără organizare sau grupare, media sa aritmetică este calculată după cum urmează:

Și în notație de însumare:

Exemplu
Proprietarii unui han turistic montan intenționează să știe câte zile stau în medie vizitatorii în facilități. Pentru aceasta, s-a păstrat o evidență a zilelor de permanență a 20 de grupuri de turiști, obținând următoarele date:
1; 1; Două; Două; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; Două; Două; 3; 4; 1
Numărul mediu de zile în care stau turiștii este:

-
Media aritmetică pentru datele grupate
Dacă datele variabilei sunt organizate într-un tabel al frecvențelor absolute feu iar centrele de clasă sunt x1, XDouă,..., Xn, media se calculează prin:

În notație de însumare:

Median
Mediana unui grup de n valori ale variabilei x este valoarea centrală a grupului, cu condiția ca valorile să fie ordonate în ordine crescătoare. În acest fel, jumătate din toate valorile sunt mai mici decât modul și cealaltă jumătate sunt mai mari..
-
Mediană a datelor negroupate
Pot apărea următoarele cazuri:
-Numărul n de valori ale variabilei x ciudat: mediana este valoarea care se află chiar în mijlocul grupului de valori:

-Numărul n de valori ale variabilei x pereche: în acest caz, mediana este calculată ca medie a celor două valori centrale ale grupului de date:

Exemplu
Pentru a găsi mediana datelor din pensiunea turistică, acestea sunt mai întâi comandate de la cel mai mic la cel mai mare:
1; 1; 1; 1; 1; 1; 1; Două; Două; Două; Două; 3; 3; 3; 4; 4; 4; 4; 5; 5
Numărul de date este egal, prin urmare există două date centrale: X10 și Xunsprezece și întrucât ambele valorează 2, media lor este, de asemenea.
Mediană = 2
-
Mediana datelor colectate
Se folosește următoarea formulă:

Simbolurile din formulă înseamnă:
-c: lățimea intervalului care conține mediana
-BM: limita inferioară a aceluiași interval
-Fm: numărul de observații cuprinse în intervalul la care aparține mediana.
-n: date totale.
-FBM: numărul de observații inainte de a intervalului care conține mediana.
Modă
Modul pentru datele negroupate este valoarea cu cea mai mare frecvență, în timp ce pentru datele grupate este clasa cu cea mai mare frecvență. Moda este considerată cea mai reprezentativă dată sau clasă a distribuției.
Două caracteristici importante ale acestei măsuri sunt că un set de date poate avea mai mult de un mod, iar modul poate fi determinat atât pentru date cantitative cât și calitative..
Exemplu
Continuând cu datele paradorului turistic, cel care se repetă cel mai mult este 1, prin urmare, cel mai obișnuit lucru este că turiștii stau o zi în parador.
Măsuri de dispersie
Măsurile de dispersie descriu modul în care datele sunt grupate în jurul măsurilor centrale.
Rang
Se calculează prin scăderea celor mai mari date și a celor mai mici date. Dacă această diferență este mare, este un semn că datele sunt împrăștiate, în timp ce valorile mici indică faptul că datele sunt apropiate de medie..
Exemplu
Gama pentru datele paradorului turistic este:
Gama = 5−1 = 4
Varianța
-
Varianța pentru datele negroupate
Pentru a găsi varianța sDouă Este necesar să se cunoască mai întâi media aritmetică, apoi se calculează diferența pătrată între fiecare bucată de date și media, toate acestea fiind adăugate și împărțite la numărul total de observații. Aceste diferențe sunt cunoscute sub numele de abateri.

Varianța, care este întotdeauna pozitivă (sau zero), indică cât de departe sunt observațiile de medie: dacă varianța este mare, valorile sunt mai dispersate decât atunci când varianța este mică.
Exemplu
Varianța pentru datele de la pensiunea turistică este:
1; 1; Două; Două; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; Două; Două; 3; 4; 1

-
Varianța pentru datele grupate
Pentru a găsi varianța unui set de date grupate, sunt necesare următoarele: i) media, ii) frecvența feu care reprezintă datele totale din fiecare clasă și iii) xeu sau valoarea clasei:

Abaterea standard este rădăcina pătrată pozitivă a varianței, deci are un avantaj față de varianță: vine în aceleași unități ca variabila studiată și astfel aveți o idee mai directă despre cât de aproape sau de departe este variabila din medie.
-
Abaterea standard pentru datele negroupate
Se determină pur și simplu prin găsirea rădăcinii pătrate a varianței pentru datele negroupate:

Abaterea standard pentru datele de la pensiunea turistică este:
s = √ (sDouă) = √1.95 = 1.40
-
Abaterea standard pentru datele grupate
Se calculează prin găsirea rădăcinii pătrate a varianței pentru datele grupate:

Măsurători de poziție
Măsurile de poziție împart un set ordonat de date în bucăți de dimensiuni egale. Mediana, pe lângă faptul că este o măsură a tendinței centrale, este și o măsură a poziției, deoarece împarte întregul în două părți egale. Dar părți mai mici pot fi obținute cu quartile, decile și percentilele.
Quartile
Cvartilele împart setul în patru părți egale, fiecare conținând 25% din date. Sunt notate ca Q1, ÎDouă și Q3 iar mediana este quartila QDouă. În acest fel, 25% din date se află sub quartila Q.1, 50% sub quartila QDouă sau median și cu 75% sub quartila Q3.

-
Cvartile pentru date negroupate
Datele sunt ordonate și totalul este împărțit în 4 grupuri cu același număr de date fiecare. Poziția primei quartile se găsește prin:
Î1 = (n + 1) / 4
Unde n este datele totale. Dacă rezultatul este un număr întreg, datele corespunzătoare poziției respective sunt localizate, dar dacă sunt zecimale, datele corespunzătoare părții întregi sunt calculate cu următoarea sau, pentru o mai mare precizie, se interpolează liniar între datele respective.
Exemplu
Poziția primului quartile Q1 pentru datele paradorului turistic este:
Î1 = (n + 1) / 4 = (20 + 1) / 4 = 5,25
Aceasta este poziția quartilei 1 și, din moment ce rezultatul este zecimal, se caută datele X.5 și X6, care sunt respectiv X5 = 1 și X6 = 1 și sunt medii, rezultând:
Prima quartilă = 1
1; 1; 1; 1; 1; 1; 1; Două; Două; Două; Două; 3; 3; 3; 4; 4; 4; 4; 5; 5.
Poziția celui de-al doilea quartile QDouă este:
ÎDouă = 2 (n + 1) / 4 = 10,5
Care este media dintre X10 și Xunsprezece și se potrivește cu mediana:
Al doilea quartile = Median = 2
Poziția celui de-al treilea quartil este calculată prin:
Î3 = 3 (n + 1) / 4 = 3 (20 + 1) / 4 = 15,75
De asemenea, este zecimal, prin urmare X este calculat cu mediecincisprezece și X16:
1; 1; 1; 1; 1; 1; 1; Două; Două; Două; Două; 3; 3; 3; 4; 4; 4; 4; 5; 5.
Dar, deoarece ambele valorează 4:
A treia quartilă = 4
Formula generală pentru poziția quartilelor în datele negroupate este:
Îk = k (n + 1) / 4
Cu k = 1,2,3.
-
Cvartile pentru date grupate
Acestea sunt calculate într-un mod similar cu mediana:

Explicația simbolurilor este:
-BÎ: limita inferioară a intervalului care conține quartila
-c: lățimea intervalului respectiv
-Fce: numărul de observații conținute în intervalul de quartile.
-n: date totale.
-FBQ: numărul de date inainte de a intervalului care conține quartila.
Decile și percentile
Decilele și percentilele împart setul de date în 10 părți egale și respectiv 100 părți egale, iar calculul lor se efectuează într-un mod similar cu cel al quartilelor.
-
Decile și percentile pentru date negroupate
Se folosesc respectiv formulele:
Dk = k (n + 1) / 10
Cu k = 1,2,3 ... 9.
Decile D5 trebuie să fie egală cu mediana.
Pk = k (n + 1) / 100
Cu k = 1,2,3 ... 99.
Percentila Pcincizeci trebuie să fie egală cu mediana.
Exemplu
În exemplul pensiunii turistice, poziția D3 este:
D3 = 3 (20 + 1) / 10 = 6,3
Deoarece este un număr zecimal, se calculează X6 și X7, ambele egale cu 1:
1; 1; 1; 1; 1; 1; 1; Două; Două; Două; Două; 3; 3; 3; 4; 4; 4; 4; 5; 5
Înseamnă că 3 zecimi din date sunt sub X7 = 1 și restul de mai sus.
-
Decile și percentile pentru date grupate
Formulele sunt analoage cu cele pentru quartile. D este folosit pentru a indica decile și P pentru percentile, iar simbolurile sunt interpretate în mod similar:

Regula empirică
Când datele sunt distribuite simetric și distribuția este unimodală, există o regulă numită regula empirică sau regula 68 - 95 - 99, care le grupează în următoarele intervale:
- 68% din date se află în intervalul:

- 95% din date se află în intervalul:

- 99% din date se află în intervalul:

Exemplu
În ce interval este 95% din datele din paradorul turistic?
Sunt în intervalul: [2,5−1,40; 2,5 + 1,40] = [1,1; 3.9].
Referințe
- Berenson, M. 1985. Statistici pentru management și economie. Interamericana S.A.
- Devore, J. 2012. Probabilități și statistici pentru inginerie și știință. A 8-a. Ediție. Cengage.
- Levin, R. 1988. Statistici pentru administratori. Al 2-lea. Ediție. Prentice hall.
- Spiegel, M. 2009. Statistici. Seria Schaum. Al 4-lea Ediție. Dealul Mcgraw.
- Walpole, R. 2007. Probabilități și statistici pentru inginerie și științe. Pearson.



Nimeni nu a comentat acest articol încă.