Modelul atomic Bohr este concepția fizicianului danez Niels Bohr (1885-1962) asupra structurii atomului, publicată în 1913. În atomul Bohr, electronii din jurul nucleului ocupă doar anumite orbite permise, datorită unei restricții numite cuantizare.
Pentru Bohr, imaginea atomului ca un sistem solar în miniatură, cu electroni care orbitează în jurul nucleului, nu era pe deplin compatibilă cu faptul că sarcinile electrice, atunci când sunt accelerate, radiază energie..
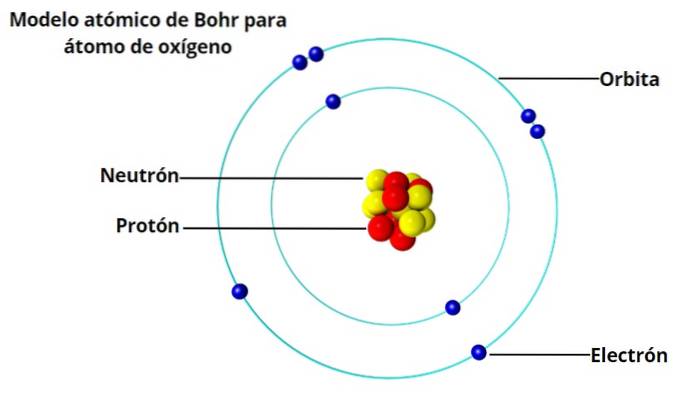
Un astfel de atom nu ar fi stabil, deoarece ar ajunge să se prăbușească mai devreme sau mai târziu, deoarece electronii ar spirala spre nucleu. Și până atunci, modelele caracteristice de lumină pe care hidrogenul și alte gaze le emit atunci când sunt încălzite erau cunoscute de 50 de ani..
Modelul sau spectrul constă dintr-o serie de linii luminoase de anumite lungimi de undă foarte specifice. Iar atomul de hidrogen nu se prăbușește din emisia de lumină.
Pentru a explica de ce atomul este stabil în ciuda faptului că poate radia energie electromagnetică, Bohr a propus că impulsul unghiular ar putea adopta doar anumite valori și, prin urmare, și energie. Aceasta este ceea ce se înțelege prin cuantizare.
Acceptând că energia a fost cuantificată, electronul ar avea stabilitatea necesară pentru a nu se repezi spre nucleul care distruge atomul..
Iar atomul radiază energie luminoasă doar atunci când electronul trece de la o orbită la alta, întotdeauna în cantități discrete. În acest fel, se explică prezența modelelor de emisie în hidrogen..
Bohr a compus astfel o viziune a atomului prin integrarea conceptelor familiare din mecanica clasică cu cele recent descoperite, precum constanta lui Planck, fotonul, electronul, nucleul atomic (Rutherford fusese mentorul lui Bohr) și spectrele de problemă menționate anterior..
Indice articol
Modelul atomic al lui Bohr presupune că electronul se mișcă pe o orbită circulară în jurul nucleului prin acțiunea forței de atracție electrostatică a lui Coulomb și propune ca impulsul unghiular al electronului să fie cuantificat.
Să vedem cum să integrăm ambele concepte în formă matematică:
Fie L magnitudinea momentului unghiular, m masa electronului, v viteza electronului și r raza orbitei. Pentru a calcula L avem:
L = m⋅r⋅v
Bohr a propus că L este egal cu multipli întregi ai constantei h / 2π, unde h este Constanta lui Planck, introdus în urmă cu puțin timp de către fizicianul Max Planck (1858-1947) la rezolvarea problemei energiei emise de un corp negru, un obiect teoretic care absoarbe toată lumina incidentă.
Valoarea sa este h = 6.626 × 10−34 J ・ s, în timp ce un h / 2π este notat ca ħ, ce se citește „Bara H”.
Prin urmare, impulsul unghiular L rămâne:
m⋅r⋅v = nħ, cu n = 1,2, 3 ...
Și din această condiție se deduc razele orbitelor permise pentru electron, așa cum vom vedea mai jos.
În cele ce urmează vom presupune cel mai simplu dintre atomi: hidrogenul, care constă dintr-un singur proton și un electron, ambii cu o sarcină de magnitudine e.
Forța centripetă care menține electronul pe orbita sa circulară este asigurată de atracția electrostatică, a cărei magnitudine F este:
F = keDouă/ rDouă
Unde k este constanta electrostatică a legii lui Coulomb și r distanța electron-proton. Știind că într-o mișcare circulară accelerația centripetă lac este dat de raportul dintre pătratul vitezei și distanța r:
lac = vDouă / r
Prin a doua lege a lui Newton, forța netă este produsul masei m și al accelerației:
mvDouă/ r = keDouă/ rDouă
Simplificând raza r, obținem:
m⋅vDouăr = keDouă
Combinând această expresie cu cea a impulsului unghiular avem un sistem de ecuații, dat de:
1) mvDouăr = keDouă
2) r = n ħ/ mv
Ideea este de a rezolva sistemul și de a determina r, raza orbitei permise. O mică algebră elementară duce la răspuns:
r = (nħ)Două / k⋅m⋅eDouă
Cu n = 1, 2, 3, 4, 5 ...
Pentru n = 1 avem cea mai mică dintre raze, numită Raza Bohr lasau cu o valoare de 0,529 × 10−10 m. Razele celorlalte orbite sunt exprimate în termeni de lasau.
În acest fel, Bohr introduce numărul cuantic principal n, observând că razele permise sunt o funcție a constantei lui Planck, a constantei electrostatice și a masei și sarcinii electronului.
Bohr combină cu pricepere mecanica newtoniană cu noi descoperiri care au avut loc continuu în a doua jumătate a secolului al XIX-lea și începutul secolului al XX-lea. Printre acestea, conceptul revoluționar al „cuantului”, de care Planck însuși a pretins că nu este foarte convins.
Prin teoria sa, Bohr a reușit să explice în mod satisfăcător seria spectrului de hidrogen și să prezică emisiile de energie în domeniul ultraviolet și infraroșu, care nu fuseseră încă observate..
Putem rezuma postulatele sale după cum urmează:
Electronul se învârte în jurul nucleului într-o orbită circulară stabilă, cu mișcare circulară uniformă. Mișcarea se datorează atracției electrostatice pe care nucleul o exercită asupra ei.
Momentul unghiular al electronului este cuantificat în funcție de expresia:
L = mvr = nħ
Unde n este un număr întreg: n = 1, 2, 3, 4 ..., ceea ce duce la faptul că electronul poate fi doar în anumite orbite definite, ale căror raze sunt:
r = (n ħ)Două / k m eDouă
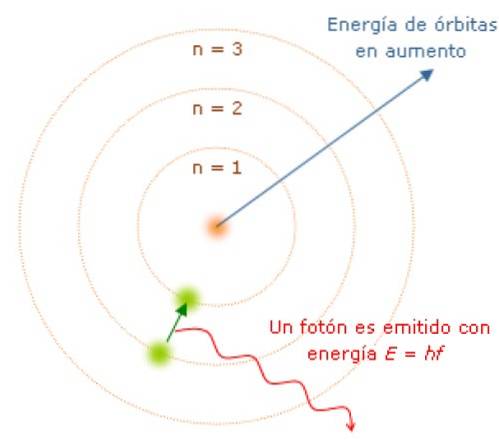
Deoarece impulsul unghiular este cuantificat, la fel este și energia E. Se poate arăta că E este dat de:
Electronul volt sau eV este o altă unitate de energie, utilizată pe scară largă în fizica atomică. Semnul negativ din energie asigură stabilitatea orbitei, indicând faptul că ar trebui să se lucreze pentru a separa electronul de această poziție..
În timp ce electronul se află pe orbita sa, acesta nu absoarbe și nu emite lumină. Dar când sare de pe o orbită de energie mai mare la una inferioară, o face..
Frecvența f a luminii emise depinde de diferența dintre nivelurile de energie ale orbitelor:
E = hf = Einiţială - Efinal
Modelul Bohr are anumite limitări:
-Se aplică cu succes doar atomului de hidrogen. Încercările de aplicare a acestuia la atomi mai complecși nu au avut succes.
-Nu răspunde de ce unele orbite sunt stabile, iar altele nu. Faptul că energia din atom a fost cuantificată a funcționat foarte bine, dar modelul nu a oferit un motiv și acest lucru a cauzat disconfort oamenilor de știință..
-O altă limitare importantă este că nu a explicat liniile suplimentare emise de atomi în prezența câmpurilor electromagnetice (efectul Zeeman și efectul Stark). Sau de ce unele linii ale spectrului au fost mai intense decât altele.
-Modelul Bohr nu ia în considerare nici efectele relativiste, pe care este necesar să le luăm în considerare, deoarece s-a stabilit experimental că electronii sunt capabili să atingă viteze destul de apropiate de cea a luminii în vid..
-Se presupune că este posibil să se cunoască cu precizie poziția și viteza electronului, dar ceea ce se calculează de fapt este probabilitatea ca electronul să ocupe o anumită poziție.
În ciuda limitărilor sale, modelul a avut un mare succes la acea vreme, nu numai pentru integrarea descoperirilor noi cu elemente deja cunoscute, ci și pentru că a ridicat noi întrebări, făcând clar că calea către o explicație satisfăcătoare a atomului stă în mecanica cuantică..
Modelul atomic al lui Schrödinger.
Modelul atomic de Broglie.
Modelul atomic Chadwick.
Modelul atomic Heisenberg.
Modelul atomic al lui Perrin.
Modelul atomic al lui Thomson.
Model atomic Dalton.
Model atomic Dirac Jordan.
Model atomic al lui Democrit.
Modelul atomic al lui Leucipp.
Modelul atomic Sommerfeld.
Modelul atomic actual.
Nimeni nu a comentat acest articol încă.