
Formule de mișcare circulară uniformă (M.C.U.), caracteristici

O particulă are mișcare circulară uniformă (M.C.U.) atunci când traiectoria sa este o circumferință și, de asemenea, o parcurge cu viteză constantă. Multe obiecte, cum ar fi părțile mașinilor și motoarelor, de exemplu, au acest tip de mișcare, printre care se evidențiază hard disk-urile computerului, palele ventilatorului, arborii și multe alte lucruri..
Mișcarea circulară uniformă este, de asemenea, o bună aproximare pentru mișcarea unor corpuri cerești, cum ar fi Pământul. De fapt, orbita Pământului este eliptică, așa cum indică legile lui Kepler. Cu toate acestea, excentricitatea orbitei este mică și, ca primă aproximare, poate fi considerată circulară, ceea ce simplifică unele calcule, cum ar fi găsirea vitezei Pământului atunci când se mișcă în jurul Soarelui..
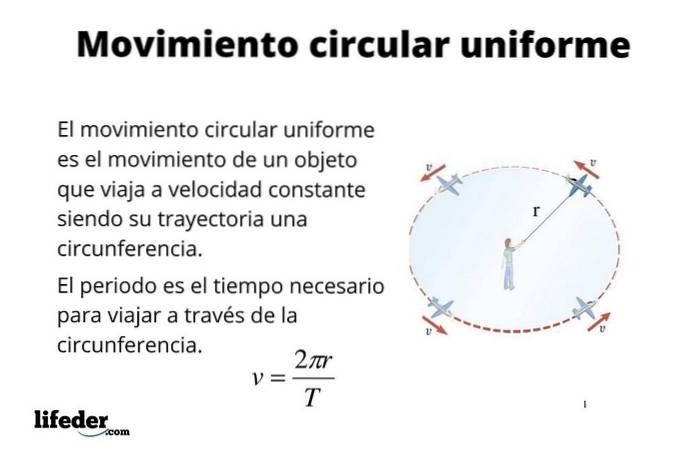
În descrierea mișcării circulare uniforme, aceiași parametri sunt folosiți ca și în mișcarea rectilinie, și anume: poziția, deplasarea, timpul, viteza și accelerația..
Accelerare? Da, într-adevăr, mișcarea circulară uniformă este accelerată, chiar dacă viteza sa v fii constant. Acest lucru se datorează faptului că viteza v, care este un vector și de aceea este îndrăzneț, schimbându-și continuu direcția pe măsură ce obiectul sau particula se rotește. Orice modificare în v este produs de o accelerație care, așa cum se va vedea, este direcționată spre centrul căii circulare.
Mișcarea circulară uniformă este mișcarea în plan X y, de aceea este o mișcare în două dimensiuni. Cu toate acestea, este posibil să o exprimăm mai confortabil prin intermediul unghiului θ pe care îl matură particula, măsurat în raport cu axa orizontală sau o altă axă de referință adecvată..
Chiar dacă este un obiect extins, particulele sale măturează întotdeauna același unghi, chiar dacă au coordonate diferite. (X y).
Indice articol
- 1 Caracteristicile mișcării circulare uniforme
- 2 Formule de mișcare circulară uniformă
- 2.1 Vectorul de poziție
- 2.2 Viteza unghiulară și viteza liniară
- 2.3 Accelerația centripetă
- 2.4 Perioada și frecvența
- 3 Exemple de mișcare circulară uniformă
- 3.1 Mișcarea Pământului
- 3.2 Particule de pe marginea unui disc
- 3.3 Telescop spațial Hubble
- 3.4 Centrifugele
- 3.5 Stropitoare de grădină
- 3.6 Sport
- 4 Exercițiul a fost rezolvat
- 5 Referințe
Caracteristicile mișcării circulare uniforme
Caracteristicile mișcării circulare uniforme pot fi rezumate după cum urmează:
-Traiectoria este o circumferință, prin urmare este o mișcare în plan.
-Viteza v este constantă, dar viteza v nu, deoarece schimbă continuu direcția și direcția pentru a se potrivi cu rotația mobilului.
-Vectorul vitezei v este întotdeauna tangențială la circumferință și perpendiculară pe direcția radială.
-Viteza unghiulară ω este constantă.
-Deși este uniform, există o accelerație pentru a explica aceste schimbări în direcția vitezei. Această accelerație este accelerația centripetă.
-Accelerația și viteza centripetă sunt perpendiculare una pe cealaltă.
-Este o mișcare periodică sau repetitivă, de aceea mărimile perioadei și frecvenței sunt definite pentru aceasta.
Formule uniforme de mișcare circulară
În această schemă există o particulă P care se rotește în sens invers acelor de ceasornic cu MCU, în funcție de direcția și sensul vectorului viteză v desenat.
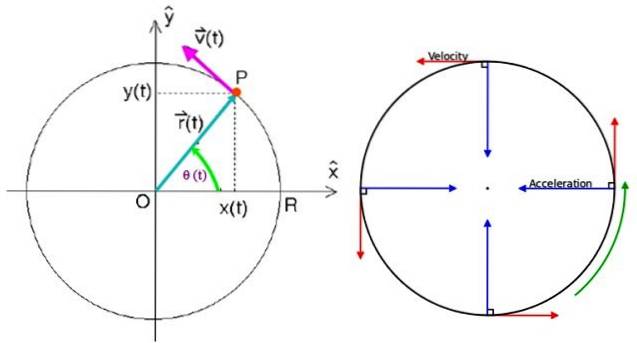
Pentru a specifica vectorul de poziție este necesar să aveți un punct de referință și punctul ideal este centrul circumferinței O care coincide cu centrul sistemului de coordonate carteziene în planul xy.
Vectorul de poziție
Este notat ca r (t) și este direcționat de la origine la punctul P unde se află particula. La un moment dat t, în coordonate carteziene, este scris ca:
r (t) = x (t) eu + Si t) j
Unde eu Da j sunt vectorii unitari perpendiculari pe direcții X și Da respectiv. Din grafic se poate observa că modulul vectorial r (t) mereu merită R, raza circumferinței. Dacă θ este unghiul format r cu axa orizontală, poziția este, de asemenea, egală cu:
r (t) = [Rcos θ(t)] eu +[Rsen θ(t)] j
Unghiul pe care îl formează r (t) cu axa orizontală este un unghi central și valoarea sa este:
θ = s / R
Unde s este arcul de circumferință parcurs și R raza. Unghiul menționat θ este o funcție a timpului, deci poate fi scris θ = θ (t), apel poziția unghiulară.
Deoarece viteza este constantă, particula descrie unghiuri egale în timpi egali și în analogie cu mișcarea rectilinie uniformă, se scrie:
θ = θ (t) = θsau + ωt
Aici θsau este unghiul inițial măsurat în radiani față de axa de referință, poate fi 0 sau orice valoare și ω este viteza unghiulară.
Viteza unghiulară și viteza liniară
Viteza unghiulară este prima derivată a poziției unghiulare și este notată ca ω. Valoarea sa este constantă pentru o mișcare circulară uniformă, deoarece unghiuri egale sunt măturate în timpi egali. Cu alte cuvinte:

Unitățile de viteză liniară în mișcare circulară uniformă sunt aceleași ca și pentru mișcarea liniară: m / s (în sistemul internațional SI), km / h, cm / s și altele..
Accelerație centripetă
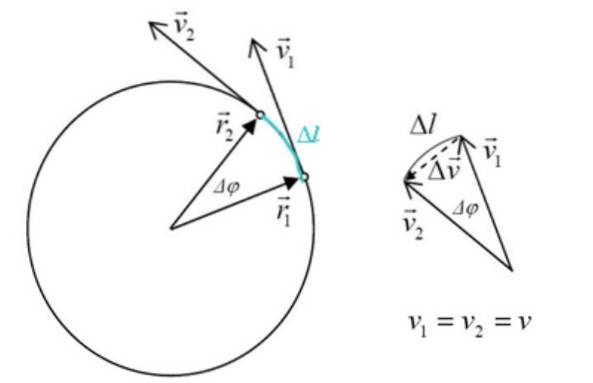
În figura de mai jos există o particulă care se mișcă în sensul acelor de ceasornic în jurul circumferinței cu viteză constantă. Aceasta înseamnă că vectorul vitezei are întotdeauna același modul, dar schimbă direcția pentru a acomoda circumferința.

Orice modificare a vitezei are ca rezultat accelerarea, care prin definiție este:

Triunghiul format din vDouă, v1 și Δv este similar cu triunghiul laturilor rDouă, r1 și Δl, unde Δφ este unghiul central. Mărimile rDouă Da r1 sunt la fel, deci:
rDouă = r1 = r
Apoi, din ambele triunghiuri avem aceste relații pentru unghiul:
Δφ = Δr / r; Δφ = Δv / v
Tipul aldin nu este necesar, deoarece măsurarea unghiului depinde de mărimile acestor vectori. Potrivind expresiile anterioare rezultă că:





Perioada și frecvența
Deoarece mișcarea circulară este repetitivă, perioada este definită T la fel ca timpul necesar mobilului pentru a face o întoarcere completă. Deoarece lungimea circumferinței razei R este de 2πR, unghiul măturat în radiani pe tura completă este de 2π radiani și necesită timp T, viteza unghiulară este:
ω = 2π / T
T = 2π / ω
Perioada de mișcare circulară uniformă este măsurată în secunde în sistemul internațional.
La rândul său, frecvența F este numărul de ture pe unitate de timp și este reciproc sau invers al perioadei:
f = n / t = 1 / T
Unitatea de frecvență în sistemul internațional este s-1.
Exemple de mișcare circulară uniformă
Multe obiecte se rotesc pentru a produce diverse efecte: roți, discuri și turbine. Odată ce viteza de funcționare este atinsă, rotația se efectuează de obicei la o viteză constantă. Mișcarea circulară este atât de obișnuită în viața de zi cu zi încât nu te gândești niciodată la asta, așa că iată câteva exemple apropiate care o ilustrează foarte bine:
Mișcarea Pământului

Pământul și celelalte planete ale sistemului solar se mișcă în traiectorii eliptice de mică excentricitate, cu excepția Mercurului, ceea ce înseamnă că, în prima aproximare, se poate presupune că mișcarea lor este circulară uniformă.
Cu aceasta, aveți o idee bună despre viteza de translație în jurul Soarelui, deoarece, în cazul Pământului, se cunoaște perioada mișcării: un an sau 365 de zile..
Particule pe marginea unui disc

Particulele care se rotesc pe marginea unui recorder vechi sau a lamei unui ventilator, urmează o mișcare circulară uniformă, odată ce dispozitivul atinge viteza de redare.
Telescop spațial Hubble

Telescopul spațial Hubble înconjoară Pământul la aproximativ 7550 m / s.
Centrifugele
Mașinile de spălat efectuează un proces de filare pentru a stoarce hainele, care constă în rotirea tamburului containerului la viteză mare. Uscătoarele se rotesc, de asemenea, o perioadă de timp cu o mișcare circulară uniformă..
Centrifugarea este, de asemenea, utilizată în laboratoare pentru a separa compușii, de exemplu, și astfel să separe constituenții lor prin diferența de densitate. Ori de câte ori vorbim despre centrifugare, există o mișcare circulară care este uniformă, cel puțin pentru un timp.
Udative de grădină
Multe aspersoare de grădină se rotesc cu o viteză constantă, astfel încât solul să fie udat uniform..
sport

De exemplu, în aruncarea cu ciocanul, care este o disciplină olimpică, sportivul rotește cu forță o minge de metal folosind un cablu de oțel atașat la mâner. Obiectivul este de a trimite mingea cât mai departe posibil, dar fără a părăsi o anumită zonă.
Exercițiul a fost rezolvat
O particulă se mișcă într-o circumferință de rază 2m cu o viteză constantă v = 8 m / s, în sens invers acelor de ceasornic. Inițial particula era în r = +2 j m. Calculati:
a) Viteza unghiulară ω
b) Poziția sa unghiulară θ (t)
c) Perioada de mișcare
d) Accelerația centripetă.
e) Poziția particulei după trecerea t = π / 4 s
Solutie la
Din formula v = Rω rezultă că:
ω = v / R = (8 m / s) / 2m = 4rad ∙ s-1
Soluția b
Luând axa pozitivă x ca axă de referință, particula este inițial la 90º = π / 2 radiani față de axa respectivă, deoarece afirmația spune că poziția inițială este +2 j m, adică particula este la y = 2m când mișcarea începe să urmeze.
θ = θ (t) = θsau + ωt = π / 2 + 4t
Soluția c
T = 2π / ω = 2π / 4 s = 0,5 π s
Soluția d
a = vDouă / R = (8 m / s)Două / 2 m = 32 m / sDouă
Soluția e
θ (t) = π / 2 + 4t → θ (π / 4) = π / 2 + 4 ∙ (π / 4) = 3π / 2 radiani
Aceasta înseamnă că după acel timp, particula se află în poziția y = -2m j. Are sens, deoarece t = π / 4 s este jumătate din perioadă, prin urmare particula a parcurs un unghi de 180 ° în sens invers acelor de ceasornic față de poziția sa inițială și trebuie să fie exact în poziția opusă..
Referințe
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 1. Cinematica. Editat de Douglas Figueroa (USB).
- Giambattista, A. 2010. Fizică. Al 2-lea. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 1. Pearson.
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7. Ed. Cengage Learning.
- Zapata, F. Mișcarea circulară. Recuperat de pe: francesphysics.blogspot.com.


Nimeni nu a comentat acest articol încă.