
Mișcare eliptică
Ce este mișcarea eliptică?
În mișcare eliptică, mobilul descrie o elipsă, la fel cum fac planetele în jurul Soarelui, și Luna și sateliții artificiali din jurul Pământului, pentru a numi câteva exemple familiare..
Forța care dă naștere acestei mișcări este forța gravitației, o forță centrală. Aceste tipuri de forțe sunt direcționate către (sau din) un punct fix O, iar modulul lor depinde de distanța până la acel punct. Dacă r este distanța și saur este vectorul unitar în direcția radială, forța centrală F este o funcție vectorială a formei:
F = F (r) saur
Cu unele matematici se poate arăta că mișcarea unui obiect sub acțiunea gravitației urmează una dintre aceste patru traiectorii: elipsă, circumferință, hiperbolă sau parabolă.
Caracteristicile mișcării eliptice
Unele dintre principalele caracteristici ale mișcării eliptice sub forța centrală sunt:
-Momentul unghiular cu privire la O este păstrat, numit L și care se calculează prin produsul vector între vectorii de poziție și viteză: L = r × mv, unde m reprezintă masa obiectului în mișcare.
-Orbita eliptică se află în planul determinat de vectori r Da v.
-Din conservarea impulsului unghiular așa-numitul legea zonelor, care stabilește că mobilul parcurge zone egale în timpi egali.
-Energia mecanică este, de asemenea, conservată în mișcare eliptică, dacă nu există forțe disipative.
-Timpul necesar mobilului pentru a da o orbită și energia sa totală depind doar de lungimea „a” axa semi-majoră a elipsei..
Diferențe cu mișcarea circulară
Deși atât în mișcarea circulară cât și în cea eliptică, obiectul se mișcă într-o cale închisă și repetitivă, adică periodic, există diferențe evidente între o mișcare și alta, cum ar fi:
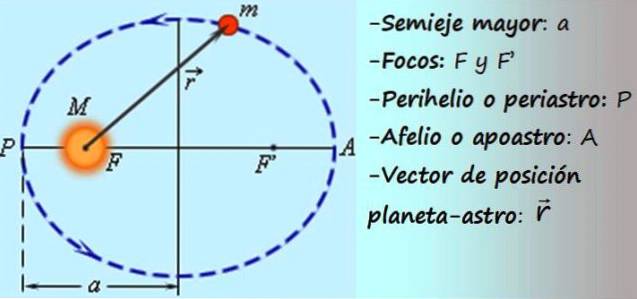
-În mișcare circulară, mobilul descrie o circumferință, a cărei rază (distanța până la centrul căii) este constantă, în timp ce în mișcare eliptică descrie o elipsă, în care distanța până la centrul căii este variabilă (vezi figura 1).
-În cazul unei mișcări circulare uniforme MCU, mobilul mătură unghiuri egale în timpi egali, dar în mișcarea eliptică planetară zone egale sunt măturate în timpi egali. Aceasta este legea zonelor, cunoscută și ca a doua lege a mișcării planetare a lui Kepler..
Ecuații importante ale mișcării eliptice planetare
Perioadă
În mișcarea eliptică derivată din atracția gravitațională, perioada T de mișcare este timpul necesar planetei sau satelitului (m) pentru a face o întoarcere eliptică în jurul Soarelui sau al Pământului (M). Aplicând conservarea energiei, rezultă că este proporțional cu cubul lungimii axei semi-majore a elipsei:

Unde G este constanta universală a gravitației: 6,67 × 10-unsprezece N ∙ mDouă/ kgDouă, M este masa Soarelui, a Pământului sau a obiectului care provoacă interacțiunea pe m și „a” este lungimea axei semi-majore.
Energie mecanică
Energia totală pentru sistemul planetei (m) - Soare (M) este:

Impuls unghiular
Mărimea impulsului unghiular într-un punct de pe orbita eliptică depinde și de lungimea axei semi-majore, precum și de excentricitatea „e”, un parametru adimensional care indică cât de aplatizată este elipsa. Dacă e = 0, elipsa devine un cerc.

Viteză
Magnitudinea vitezei este dată de următoarea ecuație:

Unde r este distanța dintre un punct de pe orbită (locația planetei) și focalizare (Soare).
Exemple de mișcare eliptică
Mișcări planetare
Prima lege a lui Kepler afirmă că mișcarea planetelor în jurul Soarelui urmează o cale eliptică, cu Soarele într-unul dintre focare. Unele comete care vizitează periodic Pământul, cum ar fi Cometa Halley, urmează și ele o mișcare eliptică..
În afară de această mișcare de translație eliptică și de rotație în jurul axei lor, planetele au propriile mișcări datorită interacțiunilor gravitaționale complexe cu celelalte planete și corpuri cerești din sistemul solar. În acest fel sunt mișcările de precesie și nutare pe care Pământul le posedă și care se datorează atracției gravitaționale comune a Soarelui și a Lunii..
În precesiune, axa Pământului descrie un con în timp ce se rotește în jurul axei perpendiculare pe plan sau ecliptică. Și în nutare, care se suprapune precesiei, axa Pământului oscilează în sus și în jos într-o buclă eliptică la fiecare 18,6 ani. În total, 1385 dintre aceste bucle în urmă în 25.767 de ani, care este perioada de precesiune a axei Pământului.
O particulă de apă oceanică
În apele oceanului, o particulă efectuează o mișcare eliptică, elipsa devenind tot mai aplatizată odată cu creșterea adâncimii. Pe de altă parte, când apele sunt adânci, mișcarea particulelor este circulară.
Ceea ce se întâmplă este că atunci când valul se apropie de coastă, forțele de frecare apar datorită apropierii sale de fund și această frecare tinde să încetinească mișcarea în partea inferioară a traiectoriei, în timp ce creasta își continuă mișcarea..
Rezultatul este că circumferința se aplatizează, iar efectul este accentuat pe măsură ce adâncimea crește..

Mod eliptic de oscilație într-un pendul fizic
Un pendul fizic constă dintr-un solid rigid care poate oscila într-un plan în jurul unei axe perpendiculare pe acesta. Dacă obiectului i se permite să se miște liber, poate descrie orice unghi în jurul axei care unește centrul de masă cu punctul de suspensie, precum și se poate roti în jurul acestuia..
Datorită rotației Pământului, pendulul este capabil să descrie orbite de formă aproximativ eliptică, care sunt cunoscute sub numele de mod eliptic de oscilație, caracterizat printr-un moment unghiular altul decât 0.
Există, de asemenea, modul plan (moment unghiular 0) și modul conic (moment unghiular altul decât 0), acesta din urmă cu o cale circulară pe un plan orizontal.
Biciclete eliptice
Mișcările eliptice descrise anterior apar în natură, dar pot fi folosite și pentru a crea obiecte utile, cum ar fi bicicletele eliptice, care sunt mașini foarte populare pentru practicarea aerobicului..
Sunt biciclete staționare care constau practic dintr-un ghidon și două pedale pe care persoana le activează împingându-se cu greutatea sa, descriind o elipsă cu picioarele. Aceasta este o mișcare naturală, cu impact redus, care este benefică, deoarece mișcă multe grupuri musculare în tot corpul..
Referințe
- Astronomia pentru toată lumea. Precesiune și nutare. Recuperat de pe: astronomiaparatodos.com.
- Calculul vitezei în orbite eliptice. Recuperat de pe: forum.lawebdefisica.com.
- Fowler, Michael. Orbite eliptice: Căi către planete. Recuperat de la: galileo.phys.virginia.edu.
- Hernández, J. Studiul modurilor de oscilație într-un pendul fizic simetric folosind potențialul efectiv. Recuperat de pe: scielo.org.co.
- Kittel, C. 1973. Mecanică. Curs de fizică Berkeley. Volumul 1. Ed. Reverté.
- Orbitele eliptice sub acțiunea forței centrale. Recuperat de pe: sc.ehu.es.
- Sisteme conservatoare. Recuperat de pe: dfmf.uned.es.Wikipedia. Orbita eliptică. Recuperat de pe: en.wikipedia.org.



Nimeni nu a comentat acest articol încă.