
Exemple de metode paralelograme, exerciții rezolvate
metoda paralelogramului este o metodă grafică pentru a adăuga doi vectori în plan. Este frecvent folosit pentru a găsi rezultatul a două forțe aplicate unui corp sau a două viteze, ca în cazul unui înotător care intenționează să traverseze un râu perpendicular și este deviat de curent.
Pentru a construi paralelogramul, originile vectorilor de adăugat, trasați la scară, trebuie să coincidă într-un punct.
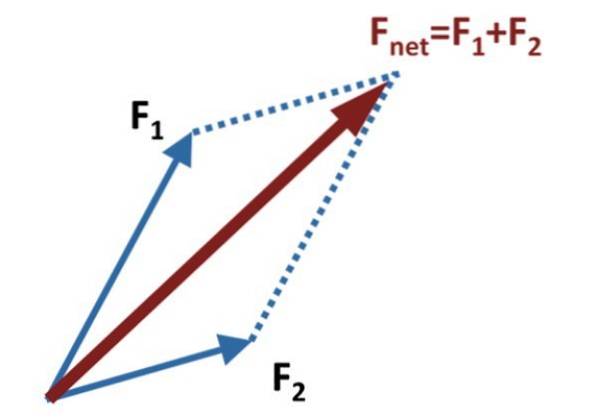
Apoi, linii auxiliare sunt trasate paralel cu fiecare vector, ajungând la capătul celuilalt, așa cum se arată în figura de mai sus.
Suma sau vectorul rezultat, numit și forța netă, este vectorul Fnet, care se obține prin desenarea vectorului care pleacă de la originea comună a F1 Da FDouă, până în punctul în care se intersectează liniile paralele auxiliare. În diagrama figurii acestea sunt reprezentate prin linii punctate.
Metoda își primește numele din figura care se formează cu vectorii de adaos și liniile auxiliare, care este tocmai un paralelogram. Diagonala principală a paralelogramului este vectorul sumă.
Este foarte important să rețineți că ordinea în care sunt așezați vectorii addend nu modifică deloc suma, deoarece această operație între vectori este comutativă.
Indice articol
- 1 Exemplu al metodei paralelogramului pas cu pas
- 1.1 Caz special: suma vectorilor perpendiculari
- 2 exerciții rezolvate
- 2.1 - Exercițiul 1
- 2.2 - Exercițiul 2
- 3 Referințe
Exemplu al metodei paralelogramului pas cu pas
Următoarea imagine prezintă vectorii v Da sau în unități arbitrare. Vectorul v măsoară 3,61 unități și formează un unghi de 56,3º cu orizontală, în timp ce sau măsoară 6,32 unități și un unghi de 18,4 ° față de linia de referință menționată.
Vom găsi suma sa vectorială folosind metoda paralelogramului.
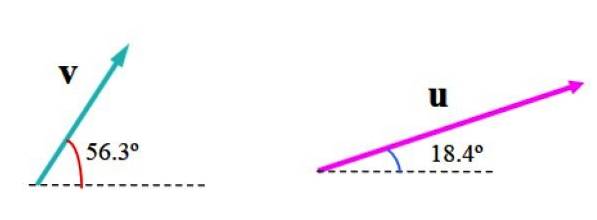
Alegeți o scară adecvată, cum ar fi cea prezentată în figura următoare, în care planul a fost împărțit de o grilă. Lățimea pătratului reprezintă o (1) unitate.
Deoarece vectorii nu sunt modificați atunci când sunt traduși, ei sunt poziționați în așa fel încât originile lor să coincidă cu originea sistemului de coordonate (imagine din stânga).
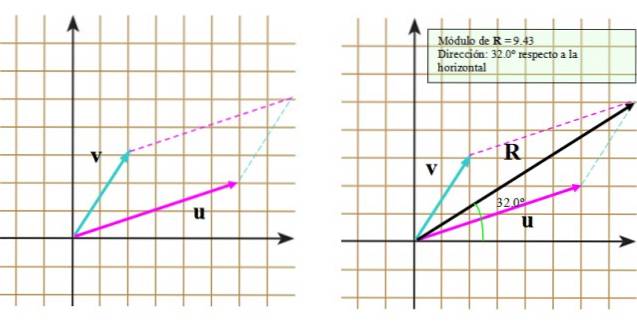
Acum să urmăm acești pași:
- Plot până la sfârșitul vectorului v o linie segmentată care este paralelă cu vectorul sau.
- Repetați procedura, dar de data aceasta cu sfârșitul vectorului sau.
- Desenați diagonala principală care se extinde de la originea comună până la punctul de intersecție al liniilor segmentate.
Rezultatul poate fi văzut în imaginea potrivită, în care apare vectorul rezultat R.
Dacă vrem să cunoaștem magnitudinea R, îi putem măsura lungimea și o putem compara cu scara pe care o avem. Și în ceea ce privește direcția sa, axa orizontală sau axa verticală pot fi folosite ca referințe, de exemplu.
Când se utilizează axa orizontală sau axa x, unghiul care R forma cu axa menționată se măsoară cu raportorul și în acest fel cunoaștem direcția R.
La fel, amploarea și direcția R poate fi calculat folosind teoremele cosinusului și sinusului, deoarece paralelogramul format poate fi împărțit în două triunghiuri congruente, ale căror laturi sunt modulele vectorilor sau, v Da R. Vezi exemplul 1 lucrat.
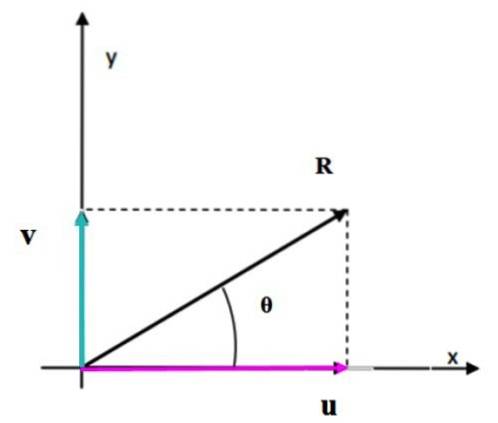
Caz special: suma vectorilor perpendiculari
Când vectorii sunt perpendiculari între ei, figura care se formează este un dreptunghi. Modulul vectorului rezultat corespunde lungimii diagonalei, care poate fi calculată cu ușurință folosind teorema lui Pitagora.
Exerciții rezolvate
- Exercitiul 1
Avem vectorul v, care măsoară 3,61 unități și formează un unghi de 56,3º cu orizontală și vectorul sau, a cărei măsură este 6,32 unități și formează un unghi de 18,4º (figura 2). Determinați modulul vectorului rezultat R = sau + v și direcția pe care vectorul o formează cu axa orizontală.
Soluţie
Metoda paralelogramului se aplică în conformitate cu pașii descriși mai sus, pentru a obține vectorul R. Așa cum am spus mai înainte, dacă vectorii sunt trasi cu atenție urmărind scara și folosind rigla și raportorul, mărimea și direcția R sunt măsurate direct pe desen.
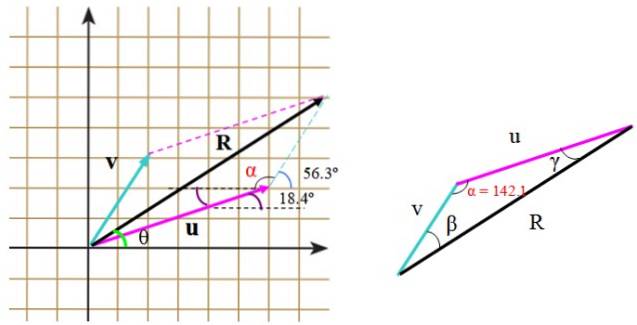
De asemenea, ele pot fi calculate direct, cu ajutorul trigonometriei și a proprietăților unghiurilor. Când triunghiul format nu este corect, ca în acest caz, se aplică teorema cosinusului pentru a găsi partea lipsă.
În triunghiul din dreapta, laturile măsoară u, v și R. Pentru a aplica teorema cosinusului este necesar să se cunoască unghiul dintre v Da sau, pe care îl putem găsi cu ajutorul grilei, poziționând corespunzător unghiurile oferite de enunț.
Acest unghi este α și este compus din:
α = (90-56,3º) + 90º + 18,4º = 142,1º
Conform teoremei cosinusului:
RDouă = vDouă + sauDouă - 2u⋅v⋅cos α = 3,61Două + 6.32Două - 2 × 3,61 × 6,32 × cos 142,1º = 88,98
R = 9,43 unități.
În cele din urmă, unghiul dintre R iar axa orizontală este θ = 18,4 º + γ. Unghiul γ poate fi găsit folosind teorema sinusului:
sin α / R = sin γ / u
Prin urmare:
sin γ = v (sin α / R) = 3,61 x (sin 142,1º / 9,43)
γ = 13,6º
θ = 18,4º + 13,6º = 32º
- Exercițiul 2
Un înotător este pe cale să traverseze un râu înot perpendicular pe curent cu o viteză constantă de 2,0 m / s. Înotătorul începe de la A, dar ajunge la B, un punct în aval, din cauza curentului care l-a deviat.
Dacă viteza curentului este de 0,8 m / s și toate vitezele sunt considerate constante, găsiți viteza înotătorului așa cum este văzută de un observator care stă pe țărm.
Soluţie
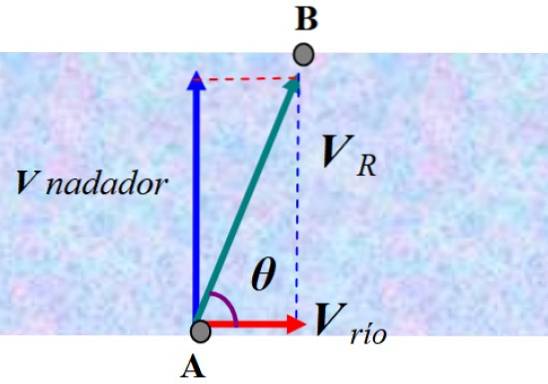
Un observator care stă pe mal ar vedea cum înotătorul este deviat în funcție de viteza rezultată VR. Pentru a găsi răspunsul, trebuie să adăugăm vectorial viteza înotătorului față de apă și viteza curentului, pe care o numim V Râu:
V R = V înotător + V Râu
În figură, care nu este la scară, vectorii au fost adăugați pentru a obține V R. În acest caz, teorema lui Pitagora poate fi aplicată pentru a obține magnitudinea sa:
VRDouă = 2,0Două + 0,8Două = 4,64
VR = 2,15 m / s
Direcția în care înotătorul se abate de la direcția perpendiculară este ușor calculată, menționând că:
θ = arctg (2 / 0,8) = 68,2º
Apoi înotătorul deviază 90º - 68,2º = 27,2º de la direcția sa inițială.
Referințe
- Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill.
- Bedford, 2000. A. Mecanica inginerească: statică. Addison Wesley.
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 1. Cinematica. Editat de Douglas Figueroa (USB).
- Giambattista, A. 2010. Fizică. Al 2-lea. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 1.


Nimeni nu a comentat acest articol încă.