
Unghiuri complementare care și cum sunt calculate, exemple, exerciții

Două sau mai multe unghiuri sunt unghiuri complementare dacă suma măsurătorilor sale corespunde cu cea a unui unghi drept. După cum se știe, măsura unghiului drept în grade este de 90 °, iar în radiani este de π / 2.
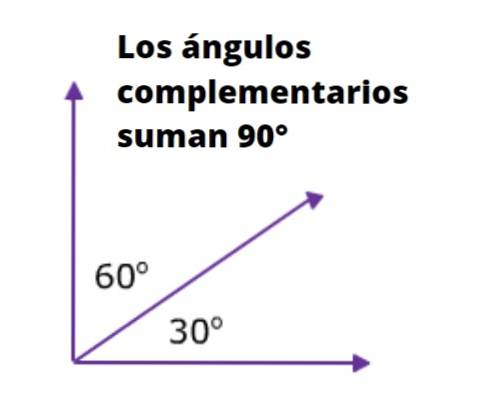
De exemplu, cele două unghiuri adiacente hipotenuzei unui triunghi dreptunghiular sunt complementare unele cu altele, deoarece suma măsurilor lor este de 90º. Următoarea figură este foarte ilustrativă în acest sens:
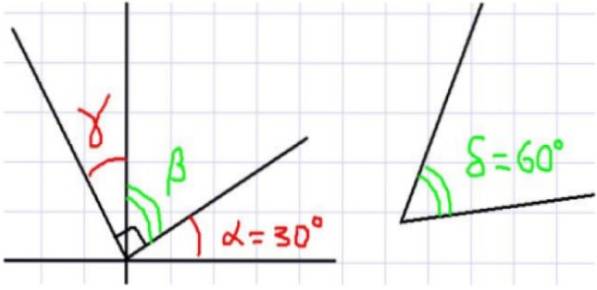
Un total de patru unghiuri sunt prezentate în figura 1. α și β sunt complementare, deoarece sunt adiacent iar suma lor completează un unghi drept. În mod similar, β este complementară cu γ, din care rezultă că γ și α sunt de aceeași măsură.
Acum, deoarece suma α și δ este egală cu 90 de grade, se poate afirma că α și δ sunt complementare. Mai mult, deoarece β și δ au aceeași α complementară, se poate afirma că β și δ au aceeași măsură.
Indice articol
- 1 Exemple de unghiuri complementare
- 1.1 - Exemplele A, B și C
- 1.2 - Exemplele D, E și F
- 2 Exerciții
- 2.1 - Exercițiul 1
- 2.2 - Exercițiul 2
- 2.3 - Exercițiul 3
- 3 unghiuri de laturi perpendiculare
- 3.1 Regula generală pentru unghiurile laterale perpendiculare
- 4 Referințe
Exemple de unghiuri complementare
În exemplele următoare se solicită găsirea unghiurilor necunoscute, marcate cu semne de întrebare în figura 2.
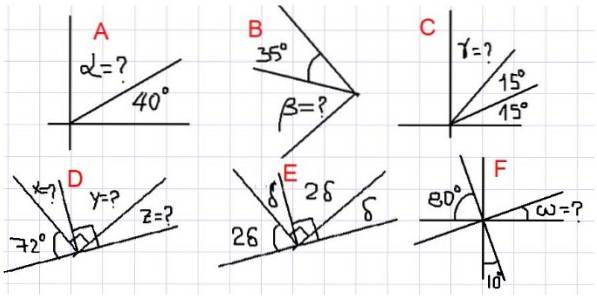
- Exemplele A, B și C
Următoarele exemple sunt în ordine de complexitate.
Exemplul A
În figura de mai sus avem că unghiurile adiacente α și 40º se adună la un unghi drept. Adică α + 40º = 90º, deci α = 90º- 40º = 50º.
Exemplul B
Deoarece β este complementar cu unghiul de 35º, atunci β = 90º - 35º = 55º.
Exemplul C
Din figura 2C avem că suma lui γ + 15º + 15º = 90º. Cu alte cuvinte, γ este complementar unghiului 30º = 15º + 15º. Astfel încât:
γ = 90º- 30º = 60º
- Exemplele D, E și F
În aceste exemple există mai multe unghiuri implicate. Pentru a găsi necunoscutele, cititorul trebuie să aplice conceptul de unghi complementar de câte ori este necesar.
Exemplul D
Deoarece X este complementar cu 72º, rezultă că X = 90º - 72º = 18º. Mai mult, Y este complementar cu X, deci Y = 90º - 18º = 72º.
În cele din urmă, Z este complementar cu Y. Din toate cele de mai sus rezultă că:
Z = 90º - 72º = 18º
Exemplul E
Unghiurile δ și 2δ sunt complementare, deci δ + 2δ = 90º.
Adică 3δ = 90º, ceea ce implică faptul că δ = 90º / 3 = 30º.
Exemplul F
Dacă numim unghiul dintre ω și 10º U, atunci U este suplimentar pentru amândouă, deoarece se observă că suma lor completează un unghi drept. Din care rezultă că U = 80º. Deoarece U este complementar cu ω, atunci ω = 10º.
Instruire
Trei exerciții sunt propuse mai jos. În toate acestea trebuie găsită valoarea unghiurilor A și B în grade, astfel încât relațiile prezentate în figura 3 să fie îndeplinite.
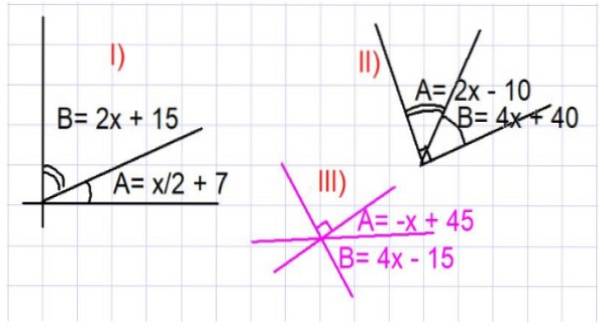
- Exercitiul 1
Determinați valorile unghiurilor A și B din partea I) din figura 3.
Soluţie
Din figura prezentată se poate observa că A și B sunt complementare, deci A + B = 90º. Înlocuim expresia pentru A și B în funcție de x dată în partea I):
(x / 2 + 7) + (2x + 15) = 90
Apoi, termenii sunt grupați corespunzător și se obține o ecuație liniară simplă:
(5x / 2) + 22 = 90
Scăzând 22 în ambii membri avem:
5x / 2 = 90 -22 = 68
Și, în cele din urmă, valoarea lui x este ștearsă:
x = 2 * 68/5 = 136/5
Acum unghiul A se găsește înlocuind valoarea lui X:
A = (136/5) / 2 +7 = 103/5 = 20,6 º.
În timp ce unghiul B este:
B = 2 * 136/5 + 15 = 347 / 5º = 69,4º .
- Exercițiul 2
Găsiți valorile unghiurilor A și B ale imaginii II, figura 3.
Soluţie
Din nou, deoarece A și B sunt unghiuri complementare, avem: A + B = 90º. Înlocuind expresia pentru A și B în funcție de x dată în partea II) din figura 3, avem:
(2x - 10) + (4x +40) = 90
Termenii asemănători sunt grupați împreună pentru a obține ecuația:
6 x + 30 = 90
Împărțind ambii membri la 6, veți obține:
x + 5 = 15
Din care rezultă că x = 10º.
Prin urmare:
A = 2 * 10 - 10 = 10º
B = 4 * 10 + 40 = 80º.
- Exercițiul 3
Determinați valorile unghiurilor A și B din partea III) din Figura 3.
Soluţie
Din nou figura este analizată cu atenție pentru a găsi unghiurile complementare. În acest caz avem acel A + B = 90 de grade. Înlocuind expresia pentru A și B în funcție de x dată în figură, avem:
(-x +45) + (4x -15) = 90
3 x + 30 = 90
Împărțirea ambilor membri la 3 rezultă în următoarele:
x + 10 = 30
De unde rezultă că x = 20º.
Cu alte cuvinte, unghiul A = -20 +45 = 25º. Și la rândul său: B = 4 * 20 -15 = 65º.
Unghiuri laterale perpendiculare
Se spune că sunt două unghiuri laturile perpendiculare dacă fiecare parte are perpendiculară corespunzătoare pe cealaltă. Următoarea figură clarifică conceptul:
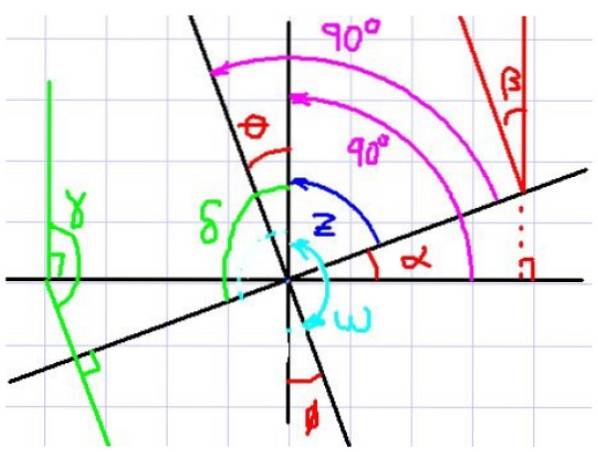
În figura 4 sunt observate unghiurile α și θ, de exemplu. Acum observați că fiecare unghi are perpendicularul său corespunzător pe celălalt unghi.
Se mai vede că α și θ au același unghi complementar z, de aceea observatorul concluzionează imediat că α și θ au aceeași măsură. S-ar părea atunci că dacă două unghiuri au laturi perpendiculare între ele, ele sunt egale, dar să ne uităm la un alt caz.
Acum considerați unghiurile α și ω. Aceste două unghiuri au, de asemenea, laturi perpendiculare corespunzătoare, totuși nu se poate spune că sunt de aceeași măsură, deoarece unul este acut și celălalt este obtuz..
Rețineți că ω + θ = 180º. Mai mult, θ = α. Dacă înlocuiți această expresie cu z în prima ecuație, veți obține:
δ + α = 180º, unde δ și α sunt unghiuri perpendiculare reciproce ale laturilor.
Regula degetului mare pentru unghiurile laturilor perpendiculare
Din cele menționate mai sus, se poate stabili o regulă care este îndeplinită atâta timp cât unghiurile au laturi perpendiculare:
Dacă două unghiuri au părți reciproc perpendiculare, atunci ele sunt egale dacă ambele sunt acute sau ambele sunt obtuse. În caz contrar, dacă una este acută și cealaltă este obtuză, atunci acestea sunt suplimentare, adică se adaugă la 180º.
Aplicând această regulă și referindu-ne la unghiurile din figura 4 putem afirma următoarele:
α = β = θ = φ
γ = δ
Cu unghiul suplimentar ω al lui α, β, θ și φ.
Referințe
- Baldor, J. A. 1973. Geometria planului și a spațiului. Cultural Central American.
- Legi și formule matematice. Sisteme de măsurare a unghiurilor. Recuperat de pe: ingemecanica.com.
- Wentworth, G. Plane Geometry. Recuperat de pe: gutenberg.org.
- Wikipedia. Unghiuri complementare. Recuperat de pe: es.wikipedia.com
- Wikipedia. Transportor. Recuperat de pe: es.wikipedia.com
- Zapata F. Goniómetro: istorie, piese, funcționare. Recuperat de pe: lifeder.com


Nimeni nu a comentat acest articol încă.