
Unghiuri în tipurile de circumferință, proprietăți, exerciții rezolvate
Chemat unghiuri de circumferință cele în care unele dintre elementele sale sunt sau se intersectează la o anumită circumferință. Printre acestea se numără următoarele:
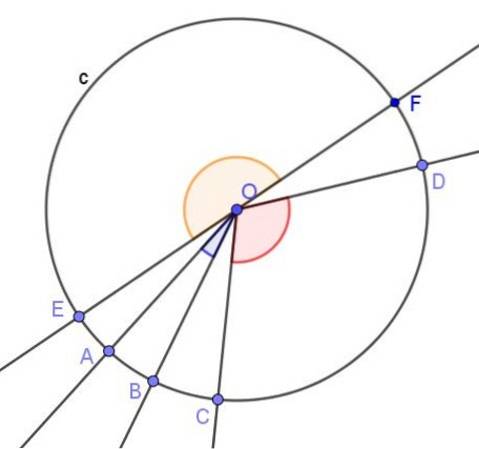
1.- unghiul central, al cărui vârf este în centrul circumferinței și laturile sale sunt secante față de acesta, așa cum vedem în următoarea imagine:

2.- The unghiul înscris, al cărui vârf este pe circumferință și laturile sale sunt secante sau tangente la circumferință.
3.- Unghi exterior, al cărui vârf este în afara circumferinței, dar laturile sale sunt secante sau tangente la circumferință.
4.- The unghiul interior, cu vârful în interiorul circumferinței și laturile sale secante la el.
Toate aceste unghiuri au anumite relații între ele și acest lucru ne conduce la proprietăți importante între unghiurile aparținând unui cerc dat.
Indice articol
- 1 Proprietăți
- 1.1 - Unghiul central
- 1.2 - Unghiul înscris
- 1.3 - Unghiul exterior
- 1.4 - Unghiul interior
- 2 exerciții rezolvate
- 2.1 - Exercițiul 1
- 2.2 - Exercițiul 2
- 3 Referințe
Proprietăți
- Unghiul central
Unghiul central este definit ca cel al cărui vârf este în centrul circumferinței și laturile sale intersectează circumferința.
Măsura în radiani a unui unghi central este coeficientul dintre arcul subtendent, adică arcul de circumferință dintre laturile unghiului și raza circumferinței.
Dacă circumferința este unitară, adică de rază 1, atunci măsura unghiului central este lungimea arcului, care corespunde numărului de radiani.
Dacă doriți măsura unghiului central în grade, înmulțiți măsura în radiani cu factorul 180º / π.
Instrumentele de măsurare a unghiului, cum ar fi transportorul și goniometrul, utilizează întotdeauna un unghi central și lungimea arcului subtend.
Acestea sunt calibrate în grade sexagesimale, ceea ce înseamnă că ori de câte ori se măsoară un unghi cu ele, în fundal ceea ce se măsoară este lungimea arcului subtins de unghiul central.
Proprietate
Măsura unui unghi central în radiani este egală cu lungimea arcului de subtendere sau de interceptare împărțit la lungimea razei.
- Unghiul înscris
Unghiul inscripționat al unui cerc este unul care are vârful pe circumferință și razele sale sunt secante sau tangente la acesta..
Proprietățile sale sunt:
Proprietăți
-Unghiul înscris este convex sau plan.
-Când un unghi inscripționat intersectează același arc ca unghiul central, măsura primului unghi va fi jumătate din cea a celui de-al doilea..
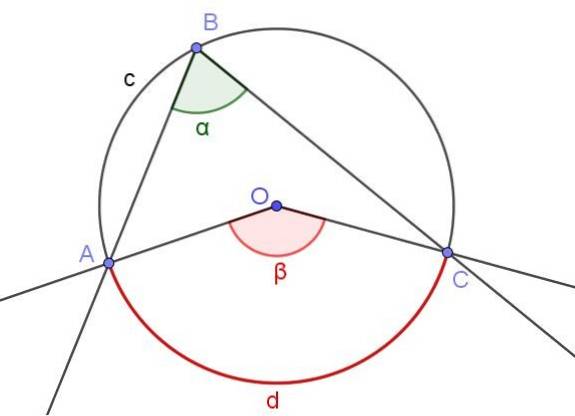
Figura 3 prezintă două unghiuri ∠ABC și ∠AOC care intersectează același arc de circumferință A⌒C.
Dacă măsura unghiului înscris este α, atunci măsura β a unghiului central este de două ori măsura unghiului înscris (β = 2 α) deoarece ambele subtend același arc de măsură d.
- Unghi exterior
Este unghiul al cărui vârf este în afara circumferinței și fiecare dintre laturile sale tăie circumferința la unul sau mai multe puncte.
Proprietate
-Măsura sa este egală cu jumătatea de diferență (sau diferența împărțită la 2) a unghiurilor centrale care interceptează aceleași arce.
Pentru a vă asigura că măsurarea este pozitivă, semidiferența trebuie să fie întotdeauna cea a celui mai mare unghi central minus măsura celui mai mic unghi central, așa cum este ilustrat în figura următoare.
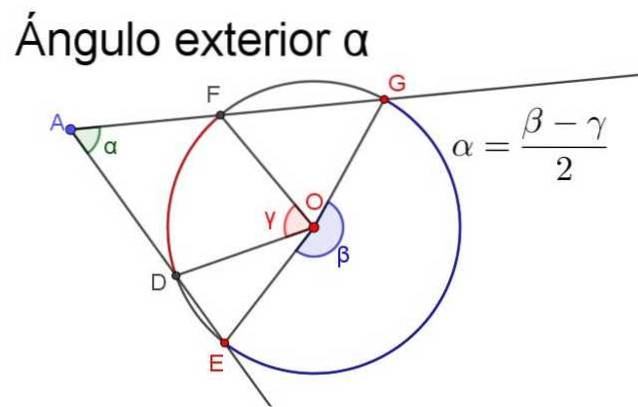
- Unghiul interior
Unghiul interior este cel al cărui vârf este în interiorul circumferinței, iar laturile sale intersectează circumferința.
Proprietate
Măsura sa este egală cu semi-suma unghiului central care subtinde același arc, plus unghiul central care subtend același arc ca unghiul său de extensie (acesta este unghiul interior format de razele complementare cu cele ale unghiului interior original ).
Următoarea figură ilustrează și clarifică proprietatea unghiului interior.
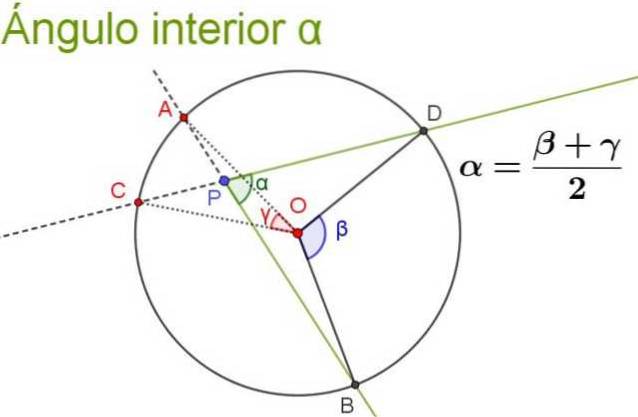
Exerciții rezolvate
- Exercitiul 1
Să presupunem un unghi inscripționat în care una dintre laturile sale trece prin centrul cercului, așa cum se arată în Figura 6. Raza cercului este OA = 3 cm și arcul d are o lungime de π / 2 cm. Determinați valoarea unghiurilor α și β.
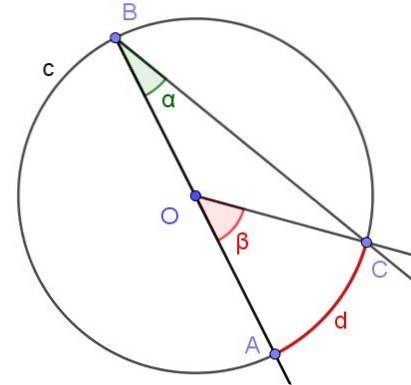
Soluţie
În acest caz, triunghiul isoscel COB este format, deoarece [OC] = [OB]. Într-un triunghi isoscel unghiurile adiacente bazei sunt egale, deci ∠BCO = ∠ABC = α. Pe de altă parte ∠COB = 180º - β. Având în vedere suma unghiurilor interne ale triunghiului COB, avem:
α + α + (180º - β) = 180º
Din care rezultă că 2 α = β, sau ceea ce este echivalent α = β / 2, cu care este confirmată proprietatea (3) secțiunii anterioare, că măsura unghiului înscris este jumătate din unghiul central, atunci când ambele unghiuri subtend același acord [AC].
Acum procedăm la determinarea valorilor numerice: unghiul β este central și măsura sa în radiani este coeficientul dintre arcul d și raza r = OA, deci măsura sa este:
β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.
Pe de altă parte, se afirmase deja că α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º.
- Exercițiul 2
În figura 7 unghiurile α1 și βDouă au aceeași măsură. Mai mult, unghiul β1 măsoară 60º. Determinați unghiurile β și α.
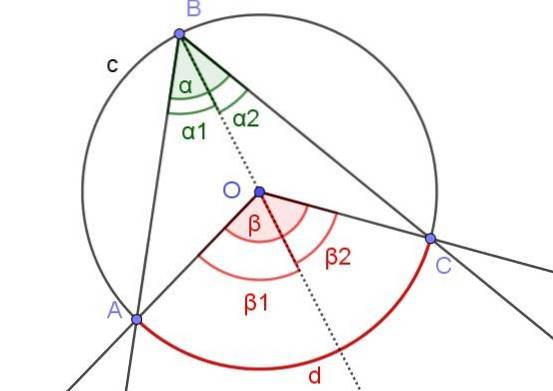
Soluţie
În acest caz avem un unghi inscripționat ∠ABC în care centrul O al circumferinței este în interiorul unghiului.
Datorită proprietății (3) avem αDouă = βDouă / 2 și α1 = β1 /Două. Ce:
α = α1 + αDouă și β = β1 + βDouă
Prin urmare, rezultă că:
α = α1 + αDouă = β1 / 2 + pDouă / 2 = (β1 + βDouă) / 2 = β / 2.
Adică, în funcție de proprietăți:
α = β / 2
Din moment ce ni se spune că β1 = 60º apoi:
α1 = β1 / 2 = 60º / 2 = 30º.
De asemenea, ne spun că α1 = βDouă deci rezultă că:
βDouă = 30º.
Unghiul β rezultă:
β1 + βDouă = 60º + 30º = 90º.
Și din moment ce α = β / 2, atunci:
α = 90º / 2 = 45º.
În concluzie:
β = 90º și α = 45º.
Referințe
- Baldor, A. 1973. Geometrie și trigonometrie. Editura Culturală din America Centrală.
- E. A. 2003. Elemente de geometrie: cu exerciții și geometrie a busolei. Universitatea din Medellin.
- Geometrie 1 ESO. Unghiuri pe circumferință. Recuperat de la: edu.xunta.es.
- Toată Știința. S-au rezolvat probleme ale unghiurilor din circumferință. Recuperat de pe: francesphysics.blogspot.com
- Wikipedia. Unghiul înscris. Recuperat de pe: es.wikipedia.com



Nimeni nu a comentat acest articol încă.