
Unghiuri suplimentare care sunt acestea, calcul, exemple, exerciții
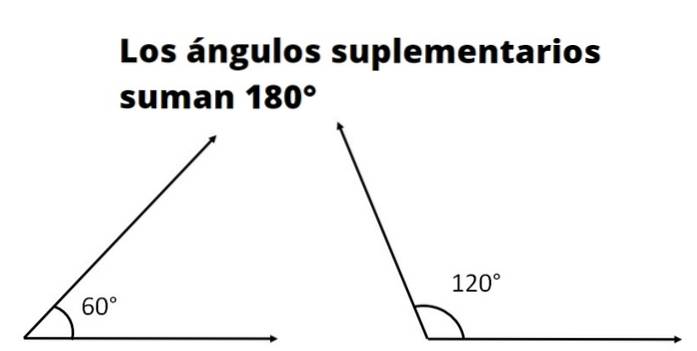
Două sau mai multe sunt unghiuri suplimentare dacă suma măsurilor sale corespunde măsurii unui unghi drept. Măsura unui unghi drept, numit și unghi plan, în grade este de 180 °, iar în radiani este π.
De exemplu, descoperim că cele trei unghiuri interioare ale unui triunghi sunt suplimentare, deoarece suma măsurilor lor este de 180º. Trei unghiuri sunt prezentate în Figura 1. Din cele de mai sus rezultă că α și β sunt suplimentare, deoarece sunt adiacente și suma lor completează un unghi drept.
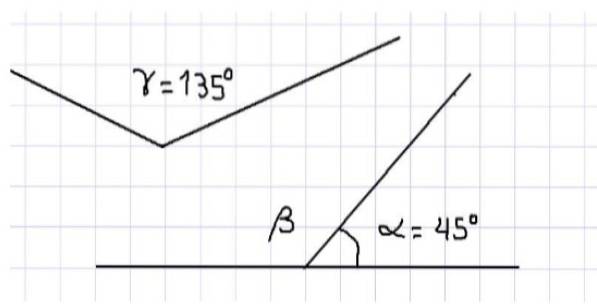
De asemenea, în aceeași figură, avem unghiurile α și γ care sunt, de asemenea, suplimentare, deoarece suma măsurilor lor este egală cu măsura unui unghi plan, adică 180º. Nu se poate spune că unghiurile β și γ sunt suplimentare deoarece, deoarece ambele unghiuri sunt obtuse, măsurile lor sunt mai mari de 90 ° și, prin urmare, suma lor depășește 180 °.
Pe de altă parte, se poate afirma că măsura unghiului β este egală cu măsura unghiului γ, deoarece dacă β este suplimentară la α și γ este suplimentară la α, atunci β = γ = 135º.
Indice articol
- 1 Exemple
- 1.1 Exemplul A
- 1.2 Exemplul B
- 1.3 Exemplul C
- 1.4 Exemplul D
- 1.5 Exemplul E
- 1.6 Exemplul F
- 2 Exerciții
- 2.1 - Exercițiul I
- 2.2 - Exercițiul II
- 2.3 - Exercițiul III
- 3 Unghiuri suplimentare în două paralele tăiate de o secantă
- 3.1 - Exercițiul IV
- 4 Referințe
Exemple
În exemplele următoare, se solicită găsirea unghiurilor necunoscute, indicate cu semne de întrebare în figura 2. Acestea variază de la cele mai simple exemple la unele puțin mai elaborate, astfel încât cititorul să fie mai atent..
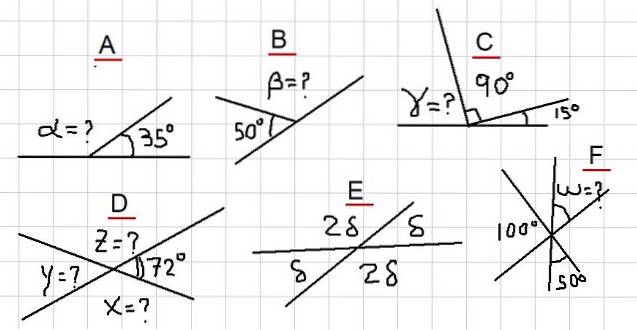
Exemplul A
În figură avem că unghiurile adiacente α și 35º se adună la un unghi plan. Adică, α + 35º = 180º și, prin urmare, este adevărat că: α = 180º- 35º = 145º.
Exemplul B
Deoarece β este suplimentar cu unghiul de 50º, atunci rezultă că β = 180º - 50º = 130º.
Exemplul C
Din figura 2C se observă următoarea sumă: γ + 90º + 15º = 180º. Adică, γ este suplimentar cu unghiul 105º = 90º + 15º. Se concluzionează atunci că:
γ = 180º- 105º = 75º
Exemplul D
Deoarece X este suplimentar la 72º, rezultă că X = 180º - 72º = 108º. Mai mult, Y este suplimentar cu X, deci Y = 180º - 108º = 72º.
Și, în cele din urmă, Z este suplimentar cu 72º, deci Z = 180º - 72º = 108º.
Exemplul E
Unghiurile δ și 2δ sunt suplimentare, deci δ + 2δ = 180º. Ceea ce înseamnă că 3δ = 180º, iar acest lucru la rândul nostru ne permite să scriem: δ = 180º / 3 = 60º.
Exemplul F
Dacă numim unghiul între 100º și 50º U, atunci U le este suplimentar, deoarece se observă că suma lor completează un unghi plan.
Urmează imediat că U = 150º. Deoarece U este opus de vârf la W, atunci W = U = 150º.
Instruire
Trei exerciții sunt propuse mai jos, în toate acestea trebuie găsită valoarea unghiurilor A și B în grade, astfel încât să se îndeplinească relațiile prezentate în figura 3. Conceptul de unghiuri suplimentare este utilizat în rezolvarea tuturor..
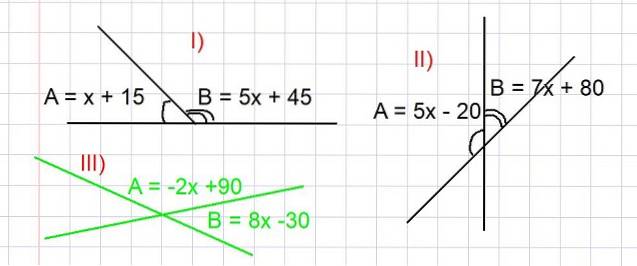
- Exercițiul I
Determinați valorile unghiurilor A și B din partea I) din figura 3.
Soluţie
A și B sunt suplimentare, din care avem acel A + B = 180 de grade, atunci expresia lui A și B este substituită în funcție de x, așa cum apare în imagine:
(x + 15) + (5x + 45) = 180
Se obține o ecuație liniară de primul ordin. Pentru a o rezolva, termenii sunt grupați imediat:
6 x + 60 = 180
Împărțind ambii membri la 6 avem:
x + 10 = 30
Și în cele din urmă rezolvând, rezultă că x valorează 20º.
Acum trebuie să conectăm valoarea lui x pentru a găsi unghiurile solicitate. Prin urmare, unghiul A este: A = 20 +15 = 35º.
Și, la rândul său, unghiul B este B = 5 * 20 + 45 = 145º.
- Exercițiul II
Găsiți valorile unghiurilor A și B din partea II) din Figura 3.
Soluţie
Deoarece A și B sunt unghiuri suplimentare, avem acel A + B = 180 de grade. Înlocuind expresia pentru A și B în funcție de x dată în partea II) din figura 3, avem:
(-2x + 90) + (8x - 30) = 180
Din nou se obține o ecuație de primul grad, pentru care termenii trebuie grupați în mod convenabil:
6 x + 60 = 180
Împărțind ambii membri la 6 avem:
x + 10 = 30
Din care rezultă că x valorează 20º.
Cu alte cuvinte, unghiul A = -2 * 20 + 90 = 50º. În timp ce unghiul B = 8 * 20 - 30 = 130º.
- Exercițiul III
Determinați valorile unghiurilor A și B din partea III) din figura 3 (în culoare verde).
Soluţie
Deoarece A și B sunt unghiuri suplimentare, avem acel A + B = 180 de grade. Trebuie să înlocuim expresia pentru A și B în funcție de x dată în figura 3, din care avem:
(5x - 20) + (7x + 80) = 180
12 x + 60 = 180
Împărțind ambii membri cu 12 pentru a rezolva valoarea lui x, avem:
x + 5 = 15
În cele din urmă, se constată că x valorează 10 grade.
Acum continuăm să înlocuim pentru a găsi unghiul A: A = 5 * 10 -20 = 30º. Și pentru unghiul B: B = 7 * 10 + 80 = 150º
Unghiuri suplimentare în două paralele tăiate de o secantă
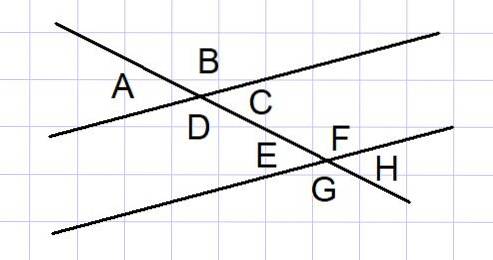
Două linii paralele tăiate de o secantă sunt o construcție geometrică obișnuită în unele probleme. Între astfel de linii, se formează 8 unghiuri așa cum se arată în figura 4.
Dintre cele 8 unghiuri, unele perechi de unghiuri sunt suplimentare, pe care le enumerăm mai jos:
- Unghiurile exterioare A și B și unghiurile exterioare G și H
- Unghiurile interioare D și C, iar unghiurile interioare E și F
- Unghiurile exterioare A și G și unghiurile exterioare B și H
- Unghiurile interioare D și E, iar interioarele C și F
Pentru completitudine, unghiurile egale între ele sunt, de asemenea, denumite:
- Alternatele interne: D = F și C = E
- Alternatele externe: A = H și B = G
- Cele corespunzătoare: A = E și C = H
- Opusurile după vârf A = C și E = H
- Cele corespunzătoare: B = F și D = G
- Opusurile după vârf B = D și F = G
- Exercițiul IV
Referindu-ne la Figura 4, care arată unghiurile dintre două linii paralele tăiate de o secantă, determinați valoarea tuturor unghiurilor în radiani, știind că unghiul A = π / 6 radiani.
Soluţie
A și B sunt unghiuri suplimentare suplimentare, deci B = π - A = π - π / 6 = 5π / 6
A = E = C = H = π / 6
B = F = D = G = 5π / 6
Referințe
- Baldor, J. A. 1973. Geometria planului și spațiului. Cultural Central American.
- Legi și formule matematice. Sisteme de măsurare a unghiurilor. Recuperat de pe: ingemecanica.com.
- Wentworth, G. Plane Geometry. Recuperat de pe: gutenberg.org.
- Wikipedia. Unghiuri suplimentare. Recuperat de pe: es.wikipedia.com
- Wikipedia. Transportor. Recuperat de pe: es.wikipedia.com
- Zapata F. Goniómetro: istorie, piese, funcționare. Recuperat de pe: lifeder.com


Nimeni nu a comentat acest articol încă.