Numere perfecte cum să le identificăm și exemple

A numărul perfect este un număr natural astfel încât suma divizorilor săi este aceeași cu numărul. Evident, numărul în sine nu poate fi inclus între divizori.

Unul dintre cele mai simple exemple de număr perfect este 6, deoarece divizorii lui sunt: ​​1, 2 și 3. Dacă adăugăm divizorii, obținem: 1 + 2 + 3 = 6.

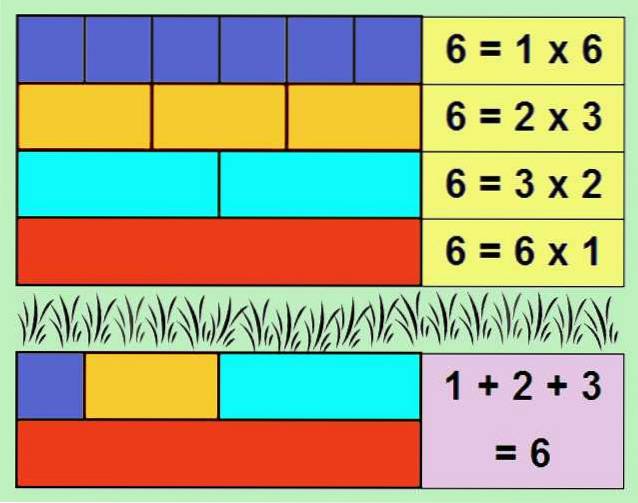
Suma divizorilor unui număr întreg, fără a include numărul în sine, se numește alicot. Prin urmare, un număr perfect este egal cu alicota sa.

Dar dacă numărul în sine este inclus în suma divizorilor unui număr, atunci un număr perfect va fi acela că suma tuturor divizorilor săi împărțită la 2 este egală cu numărul în sine..

Indice articol

• 1 Istorie
• 2 Proprietăți ale numerelor perfecte
  • 2.1 Formula și criteriul lui Euclid
  • 2.2 Cel mai mare număr perfect cunoscut
  • 2.3 Un număr perfect este prietenul cu el însuși
• 3 Exemple de numere perfecte
• 4 Exerciții
  • 4.1 - Exercițiul 1
  • 4.2 - Exercițiul 2
  • 4.3 - Exercițiul 3
  • 4.4 - Exercițiul 4
• 5 Referințe

Poveste

Matematicienii din antichitate, în special grecii, acordau o mare importanță numerelor perfecte și le atribuiau calități divine..

De exemplu, Filon din Alexandria, spre primul secol, a afirmat că 6 și 28 sunt numere perfecte care coincid cu cele șase zile de la crearea lumii și cele douăzeci și opt de zile necesare lunii pentru a înconjura Pământul..

Numerele perfecte sunt, de asemenea, prezente în natură, de exemplu, la polul nord al lui Saturn apare și numărul perfect 6, un vortex în formă de hexagon găsit de sonda Cassini și care îi intrigă pe oamenii de știință.. 

Fagurii albinelor au celule în formă hexagonală, adică cu 6 laturi. S-a arătat că poligonul cu numărul perfect 6 este cel care permite maximizarea numărului de celule din stupul de albine, cu minimul de ceară pentru elaborarea acestuia..

Proprietățile numerelor perfecte

Suma tuturor divizorilor unui număr natural n este notată cu σ (n). Într-un număr perfect se satisface că: σ (n) = 2n.

Formula și criteriile lui Euclid

Euclid a descoperit o formulă și un criteriu care permite găsirea numerelor perfecte. Această formulă este:

Două^(n-1) (Douăⁿ -1)

Cu toate acestea, numărul generat de formulă va fi perfect numai atunci când factorul (2ⁿ -1) fii văr.

Să vedem cum sunt generate primele numere perfecte:

Dacă n = 2, atunci rămânem cu 2¹ (Două^Două - 1) = 2 x 3 = 6 pe care l-am văzut deja este perfect.

Când n = 3 avem 2^Două (Două³ - 1) = 4 x 7 = 28, care este, de asemenea, perfect, așa cum este verificat în detaliu în exemplul 1.

Să vedem ce se întâmplă cu n = 4. Când înlocuim în formula lui Euclid avem:

Două³ (Două⁴ - 1) = 8 x 15 = 120

Se poate verifica că acest număr nu este perfect, așa cum se arată în detaliu în exemplul 3. Acest lucru nu contrazice criteriul lui Euclid, deoarece 15 nu este prim, o cerință necesară pentru ca rezultatul să fie un număr perfect.

Acum să vedem ce se întâmplă când n = 5. Aplicând formula pe care o avem:

Două⁴ (Două⁵ - 1) = 16 x 31 = 496

Deoarece 31 este un număr prim, atunci numărul 496 trebuie să fie perfect, conform criteriilor lui Euclid. În exemplul 4 se arată în detaliu că este într-adevăr.

Numere prime care au forma 2^p - 1 se numește veri Mersenne, după călugărul Marin Mersenne, care a studiat numerele prime și numerele perfecte încă din secolul al XVII-lea..

Mai târziu, în secolul al XVIII-lea, Leonhard Euler a arătat că toate numerele perfecte generate de formula lui Euclid sunt pare.

Până în prezent nu s-a găsit nici un perfect ciudat.

Cel mai mare număr perfect cunoscut

Până în prezent, sunt cunoscute 51 de numere perfecte, toate generate de formula și criteriul lui Euclid. Acest număr a fost obținut odată ce a fost găsit verișorul Mersenne mai mare, care este: (2^82589933 - 1).

Numărul perfect # 51 este (2^82589933) x (2^82589933 - 1) și are 49724095 cifre.

Un număr perfect este prietenul cu el însuși

În teoria numerelor se spune că două numere sunt prietene atunci când suma divizorilor unuia, fără a include numărul în sine, este egală cu celălalt număr și invers.

Cititorul poate verifica dacă suma divizorilor a 220, fără a include 220 este 284. Pe de altă parte, suma divizorilor lui 284, fără a include 284, este egală cu 220. Prin urmare, perechea de numere 220 și 284 sunt prieteni.

Din acest punct de vedere, un număr perfect este prieten cu sine..

Exemple de numere perfecte

Primele opt numere perfecte sunt enumerate mai jos:

6

28

496

8128

33550336

8589869056

137438691328

2305843008139952128

Instruire

În exercițiile următoare, va fi necesar să se calculeze divizorii unui număr, apoi să se adauge și să se verifice dacă numărul este sau nu un număr perfect..

Prin urmare, înainte de a aborda exercițiile, vom revizui conceptul și vom arăta cum sunt calculate..

Pentru început, trebuie să vă amintiți că numerele pot fi prime (atunci când pot fi împărțite exact cu el însuși și 1) sau compuse (când pot fi descompuse ca produs al numerelor prime).

Pentru un număr compus N avem:

N = aⁿ . b^m. c^p ... r^k 

Unde a, b, c ... r sunt numere prime și n, m, p ... k sunt exponenți aparținând numerelor naturale, care pot fi de la 1 încoace.

În ceea ce privește acești exponenți, există o formulă pentru a ști câți divizori are numărul N, deși nu ne spune care sunt aceștia. Fie C această cantitate, atunci:

C = (n +1) (m + 1) (p +1) ... (k + 1)

Descompunerea numărului N ca produs al numerelor prime și știind câți divizori are, atât primi, cât și neprimiți, ne va ajuta să determinăm care sunt acești divizori..

Odată ce le aveți pe toate, cu excepția ultimului care nu este necesar în sumă, puteți verifica dacă este sau nu un număr perfect.

- Exercitiul 1

Verificați dacă numărul 28 este perfect.

Soluţie

Primul lucru va fi descompunerea numărului în factorii săi primi.

28 | 2
14 | 2
07 | 7
01 | 1

Divizorii săi sunt: ​​1, 2, 4, 7, 14 și 28. Dacă excludem 28, suma divizorilor dă:

1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28

Prin urmare, 28 este un număr perfect.

Mai mult, suma tuturor divizorilor săi este 28 + 28, deci regula σ (28) = 2 x 28 este îndeplinită.

- Exercițiul 2

Decizia dacă numărul 38 este perfect sau nu.

Soluţie

Numărul este descompus în factorii săi primi:

39 | 3
13 | 13
01 | 1

Divizorii lui 39 fără a include numărul în sine sunt: ​​1, 3 și 13. Suma 1 + 3 + 13 = 4 + 13 = 17 nu este egală cu 39, prin urmare 39 este un număr imperfect sau neperfect. 

- Exercițiul 3

Aflați dacă îngerul numărul 120 este perfect sau imperfect.

Soluţie

Procedăm la descompunerea numărului în factorii săi primi:

120 | 2
060 | 2
 30 | 2
 15 | 3
  5 | 5
  1 | 1

Din factorii primi continuăm să găsim divizorii:

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 și 120

Dacă 120 ar fi perfect, adăugarea tuturor divizorilor săi ar trebui să obțină 2 x 120 = 240. 

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360

Acest rezultat este clar diferit de 240, deci se concluzionează că numărul 120 nu este un număr perfect..

- Exercițiul 4

Verificați dacă numărul 496, obținut după criteriul lui Euclid, este un număr perfect.

Soluţie

Numărul 496 se descompune în factorii săi primi:

496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1

Deci divizorii săi sunt:

1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Acum sunt adăugate toate, cu excepția 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Confirmând că este într-adevăr un număr perfect.

Referințe

1. Baldor, A. 1986. Aritmetică. Ediții și distribuții Codex.
2. Totul despre numere prime. Numere prietenoase. Recuperat de pe: numeroprimos.org.
3. Wolfram MathWorld. Regula lui Euler. Recuperat de pe: mathworld.wolfram.com.
4. Wolfram MathWorld. Număr perfect. Recuperat de pe: mathworld.wolfram.com.
5. Wikipedia. Numere perfecte. Recuperat de pe: en.wikipedia.org.
6. Wikipedia. Numere prietenoase. Recuperat de pe: es.wikipedia.org.