numere rationale sunt toate numerele care pot fi obținute ca împărțirea a două numere întregi. Exemple de numere raționale sunt: 3/4, 8/5, -16/3 și cele care apar în figura următoare. Într-un număr rațional se indică coeficientul, fiind posibil să se facă mai târziu dacă este necesar.
Figura reprezintă orice obiect, rotund pentru comoditate. Dacă vrem să îl împărțim în 2 părți egale, ca în dreapta, mai avem două jumătăți și fiecare valorează 1/2.
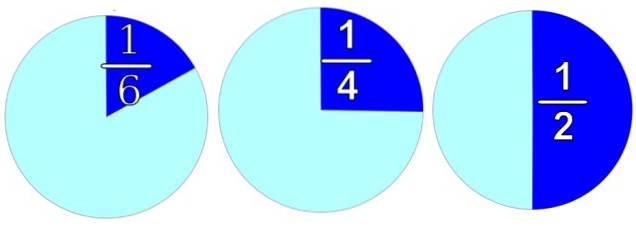
Împărțind-o în 4 părți egale, vom obține 4 bucăți și fiecare valorează 1/4, ca în imaginea din centru. Și dacă este necesar să-l distribuiți în 6 părți egale, deoarece fiecare parte ar valora 1/6, pe care o vedem în imaginea din stânga.
Desigur, l-am putea împărți și în două părți inegale, de exemplu am putea păstra 3/4 părți și economisi 1/4 părți. Sunt posibile și alte diviziuni, precum 4/6 părți și 2/6 părți. Important este că suma tuturor părților este 1.
În acest fel, este evident că, cu numere raționale, lucruri precum mâncarea, banii, pământul și tot felul de obiecte pot fi împărțite, numărate și distribuite în fracțiuni. Și astfel cantitatea de operații care se pot face cu numerele este extinsă.
Numerele raționale pot fi, de asemenea, exprimate în formă zecimală, după cum se poate vedea în următoarele exemple:
1/2 = 0,5
1/3 = 0,3333 ...
3/4 = 0,75
1/7 = 0.142857142857142857 ...
Mai târziu vom indica cum să treci de la o formă la alta cu exemple.
Indice articol
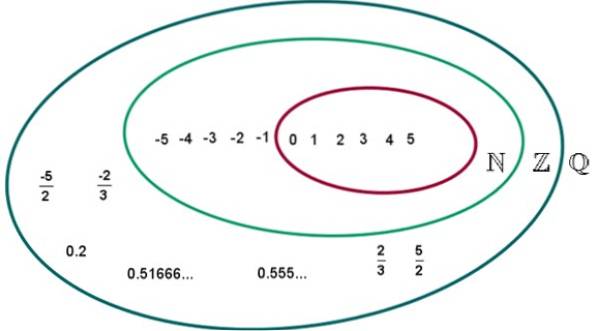
Numerele raționale, al căror set îl vom nota cu litera Q, au următoarele proprietăți:
-Q include numerele naturale N și numerele întregi Z.
Ținând cont că orice număr la Poate fi exprimat ca coeficient între el însuși și 1, este ușor de văzut că printre numerele raționale există și numere naturale și numere întregi.
Astfel, numărul natural 3 poate fi scris ca o fracție și, de asemenea, -5:
3 = 3/1
-5 = -5/1 = 5 / -1 = - (5/1)
În acest fel, Q este un set numeric care include un număr mai mare de numere, ceva foarte necesar, deoarece numerele „rotunde” nu sunt suficiente pentru a descrie toate operațiunile posibile de făcut..
-Numerele raționale pot fi adăugate, scăzute, înmulțite și împărțite, rezultatul operației fiind un număr rațional: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.
-Între fiecare pereche de numere raționale, se poate găsi întotdeauna un alt număr rațional. De fapt, între două numere raționale există numere raționale infinite.
De exemplu, între raționalele 1/4 și 1/2 se află raționalele 3/10, 7/20, 2/5 (și multe altele), care pot fi verificate exprimându-le ca zecimale.
-Orice număr rațional poate fi exprimat ca: i) un număr întreg sau ii) o zecimală limitată (strictă) sau periodică: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,166666666 ...
-Același număr poate fi reprezentat de fracții echivalente infinite și toate aparțin Q. Să vedem acest grup:
Toate reprezintă zecimalul 0,428571 ...
-Dintre toate fracțiile echivalente care reprezintă același număr, fracția ireductibilă, cea mai simplă dintre toate, este reprezentant canonic din acel număr. Reprezentantul canonic al exemplului de mai sus este 3/7.
-Fracții adecvate, acele în care numărătorul este mai mic decât numitorul:
-Fracții necorespunzătoare, al căror numărător este mai mare decât numitorul:
-Numere naturale și numere întregi:
-Fracții echivalente:
Când numeratorul este împărțit la numitor, se găsește forma zecimală a numărului rațional. De exemplu:
2/5 = 0,4
3/8 = 0,375
1/9 = 0.11111 ...
6/11 = 0,545454 ...
În primele două exemple, numărul de zecimale este limitat. Aceasta înseamnă că, atunci când se face împărțirea, obținem în cele din urmă un rest de 0.
Pe de altă parte, în următoarele două, numărul zecimalelor este infinit și de aceea sunt plasate elipsele. În acest din urmă caz există un model în zecimale. În cazul fracției 1/9, numărul 1 se repetă la nesfârșit, în timp ce în 6/11 este 54.
Când se întâmplă acest lucru, se spune că zecimalul este periodic și este notat cu un cursor de genul acesta:
Dacă este o zecimală limitată, virgula este pur și simplu eliminată și numitorul devine unitatea urmată de atâtea zerouri câte cifre există în zecimală. De exemplu, pentru a transforma zecimalul 1.26 într-o fracție, scrieți-l astfel:
1,26 = 126/100
Apoi fracția rezultată este simplificată la maxim:
126/100 = 63/50
Dacă zecimalul este nelimitat, perioada este identificată mai întâi. Apoi, acești pași sunt urmați pentru a găsi fracția rezultată:
-Numărătorul este scăderea dintre număr (fără virgulă sau caret) și partea care nu poartă accentul circumflex.
-Numitorul este un număr întreg cu atâția 9 câte cifre există sub circumflex și atât cât 0 sunt cifre în partea zecimală există care nu sunt sub circumflex.
Să urmăm această procedură pentru a transforma numărul zecimal 0.428428428 ... într-o fracție.
-În primul rând, este identificată perioada, care este secvența care se repetă: 428.
-Atunci se face operația de scădere a numărului fără virgulă sau accent: 0428 din partea care nu are circumflex, care este 0. Este astfel 428 - 0 = 428.
-Numitorul este construit, știind că sub circumflex există 3 figuri și toate sunt sub circumflex. Prin urmare, numitorul este 999.
-În cele din urmă, fracția este formată și simplificată, dacă este posibil:
0,428 = 428/999
Nu este posibil să simplificăm mai mult.
Când fracțiile au același numitor, adăugarea și / sau scăderea lor este foarte ușoară, deoarece numeratorii sunt pur și simplu adăugați algebric, lăsând același lucru cu adunările ca numitorul rezultatului. În cele din urmă, dacă este posibil, este simplificat.
Efectuați următoarea adunare algebrică și simplificați rezultatul:
Fracția rezultată este deja ireductibilă.
În acest caz, addendele sunt înlocuite cu fracții echivalente cu același numitor și apoi se urmează procedura deja descrisă.
Adăugați algebric următoarele numere raționale, simplificând rezultatul:
Pașii sunt:
-Determinați cel mai mic multiplu comun (MCM) al numitorilor 5, 8 și 3:
mcm (5,8,3) = 120
Acesta va fi numitorul fracției rezultate fără simplificare.
-Pentru fiecare fracție: împarte LCM la numitor și înmulțește cu numărătorul. Rezultatul acestei operații este plasat, cu semnul său respectiv, în numeratorul fracției. În acest fel, se obține o fracțiune echivalentă cu originalul, dar cu LCM ca numitor..
De exemplu, pentru prima fracție, numeratorul este construit astfel: (120/5) x 4 = 96 și obținem:
Procedați în același mod pentru restul fracțiilor:
În cele din urmă, fracțiile echivalente sunt substituite fără a uita semnul lor și se efectuează suma algebrică a numărătorilor:
(4/5) + (14/8) - (11/3) + 2 = (96/120) + (210/120) - (440/120) + (240/120) =
= (96 + 210-440 + 24) / 120 = -110 / 120 = -11/12
Înmulțirea și împărțirea se fac urmând regulile prezentate mai jos:
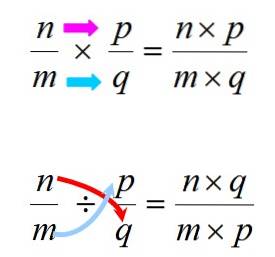
În orice caz, este important să ne amintim că multiplicarea este comutativă, ceea ce înseamnă că ordinea factorilor nu modifică produsul. Acest lucru nu se întâmplă în cazul divizării, deci trebuie să se acorde atenție respectării ordinii dintre dividend și divizor.
Efectuați următoarele operații și simplificați rezultatul:
a) (5/3) x (8/15)
b) (-4/5) ÷ (2/9)
(5/3) x (8/15) = (5 x 8) / (3 x 15) = 15/120 = 1/8
(-4/5) ÷ (2/9) = (-4 x 9) / (5 x 2) = -36 / 10 = -18/5
Luisa avea 45 de dolari. A cheltuit o zecime din ea cumpărând o carte și 2/5 din ceea ce a rămas pe un tricou. Câți bani mai au Luisa? Exprimați rezultatul ca o fracțiune ireductibilă.
Costul cărții (1/10) x 45 USD = 0,1 x 45 USD = 4,5 USD
Prin urmare, Luisa a rămas cu:
45 - 4,5 $ = 40,5 $
Cu acei bani Luisa a mers la magazinul de haine și a cumpărat cămașa, al cărei preț este:
(2/5) x 40,5 USD = 16,2 USD
Acum Luisa are în portofoliu:
40,5 - 16,2 $ = 24,3 $
Pentru a-l exprima ca o fracțiune, este scris astfel:
24,3 = 243/10
Asta este ireductibil.
Nimeni nu a comentat acest articol încă.