
Istoricul numerelor reale, exemple, proprietăți, operații

numere reale ele constituie setul numeric care include numerele naturale, numerele întregi, raționalul și iraționalul. Sunt notate cu simbolul ℝ sau pur și simplu R iar domeniul de aplicare pe care îl au în știință, inginerie și economie este de așa natură încât, atunci când vorbim de „număr”, este aproape de la sine înțeles că este un număr real.
Numerele reale au fost folosite din cele mai vechi timpuri, deși nu li s-a dat acest nume. Deja din momentul în care Pitagora și-a dezvoltat celebra teoremă, au apărut numere care nu puteau fi obținute ca niște coeficienți de numere naturale sau numere întregi.
Exemple de numere sunt √2, √3 și π. Aceste numere sunt numite iraţional, spre deosebire de numerele raționale, care provin din rapoarte întregi. Prin urmare, a fost necesar un set numeric care să cuprindă ambele clase de numere..
Termenul „număr real” a fost creat de marele matematician René Descartes (1596-1650), pentru a distinge între cele două tipuri de rădăcini care pot apărea din rezolvarea unei ecuații polinomiale.
Unele dintre aceste rădăcini pot fi chiar rădăcini ale numerelor negative, Descartes le-a numit „numere imaginare” și cele care nu erau, erau numere reale.
Denumirea a persistat de-a lungul timpului, dând naștere la două seturi numerice mari: numere reale și numere complexe, un set mai mare care include numere reale, numere imaginare și cele care sunt parțiale reale și parțial imaginare..
Evoluția numerelor reale și-a continuat cursul până când, în 1872, matematicianul Richard Dedekind (1831-1936) a definit formal setul numerelor reale prin așa-numitele tăieturi de Dedekind. Sinteza operei sale a fost publicată într-un articol care a văzut lumina în același an.
Indice articol
- 1 Exemple de numere reale
- 1.1 Reprezentarea numerelor reale pe linia reală
- 2 Proprietățile numerelor reale
- 3 Operații cu numere reale
- 4 Aplicații
- 5 Exercițiul a fost rezolvat
- 5.1 Exercițiul 1
- 6 Referințe
Exemple de numere reale
Tabelul de mai jos prezintă exemple de numere reale. Acest set are ca subseturi numerele naturale, numerele întregi, raționalul și iraționalul. Orice număr din aceste seturi este el însuși un număr real.
Prin urmare, 0, negative, pozitive, fracții și zecimale sunt numere reale.

Reprezentarea numerelor reale pe linia reală
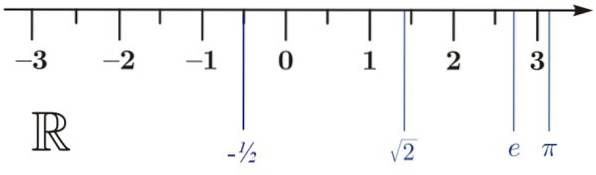
Numerele reale pot fi reprezentate pe linia reală R, așa cum arată imaginea. Nu este necesar ca 0 să fie întotdeauna prezent, totuși este convenabil să știm că în stânga sa se află realele negative și în dreapta cele pozitive. De aceea este un punct de referință excelent.
Pe linia reală se ia o scară, în care se găsesc numerele întregi:… 3, -2, -1, 1, 2, 3…. Săgeata indică faptul că linia se extinde până la infinit. Dar asta nu este tot, în orice interval considerat, vom găsi întotdeauna și numere reale infinite.
Numerele reale sunt reprezentate în ordine. Pentru început, există ordinea numerelor întregi, în care pozitivele sunt întotdeauna mai mari decât 0, în timp ce negativele sunt mai mici..
Această ordine este păstrată în numerele reale. Următoarele inegalități sunt prezentate ca exemplu:
a) -1/2 < √2
fi < π
c) π> -1/2
Proprietățile numerelor reale
-Numerele reale includ numere naturale, numere întregi, numere raționale și numere iraționale..
-Proprietatea comutativă a adunării este îndeplinită: ordinea suplimentelor nu modifică suma. Dacă a și b sunt două numere reale, este întotdeauna adevărat că:
a + b = b + a
-0 este elementul neutru al sumei: a + 0 = a
-Pentru suma proprietatea asociativă este satisfăcută. Dacă a, b și c sunt numere reale: (a + b) + c = a + (b + c).
-Opusul unui număr real la este -a.
-Scăderea este definită ca suma opusului: a - b = a + (-b).
-Proprietatea comutativă a produsului este satisfăcută: ordinea factorilor nu modifică produsul: a.b = b.a
-În produs se aplică și proprietatea asociativă: (a.b) .c = a. (B.c)
-1 este elementul neutru al înmulțirii: a.1 = a
-Proprietatea distributivă a multiplicării cu privire la adunare este valabilă: a. (b + c) = a.b + a.c
-Diviziunea cu 0 este nedefinită.
-Orice număr real a, cu excepția 0, are un invers multiplicativ de-1 astfel încât a.a-1 = 1.
-Dacă a este un număr real: a0 = 1 și a1 = a.
-Valoarea absolută sau modulul unui număr real este distanța dintre numărul respectiv și 0.
Operații cu numere reale
Cu numerele reale puteți face operațiile care se fac cu celelalte seturi numerice, inclusiv adunarea, scăderea, înmulțirea, divizarea, împuternicirea, radicația, logaritmii și multe altele.
Ca întotdeauna, diviziunea cu 0 nu este definită, nici logaritmii negativi ai numerelor și nici 0, deși este adevărat că log 1 = 0 și că logaritmii numerelor între 0 și 1 sunt negative.
Aplicații
Aplicațiile numerelor reale la tot felul de situații sunt extrem de variate. Numerele reale apar ca răspunsuri la multe probleme din știința exactă, informatică, inginerie, economie și științe sociale..
Toate tipurile de mărimi și cantități, cum ar fi distanțele, timpii, forțele, intensitatea sunetului, banii și multe altele, își au expresia în număr real.
Transmiterea semnalelor telefonice, imaginea și sunetul unui videoclip, temperatura unui aparat de aer condiționat, a unui încălzitor sau a unui frigider pot fi controlate digital, ceea ce înseamnă transformarea mărimilor fizice în secvențe numerice.
Același lucru se întâmplă atunci când faceți o tranzacție bancară pe Internet sau consultați mesageria instantanee. Numerele reale sunt peste tot.
Exercițiul a fost rezolvat
Vom vedea cu exerciții cum funcționează aceste numere în situații comune pe care le întâlnim zilnic..
Exercitiul 1
Oficiul poștal acceptă doar pachete pentru care lungimea, plus măsurarea circumferinței, nu depășește 108 inci. Prin urmare, pentru ca pachetul afișat să fie acceptat, trebuie să se îndeplinească faptul că:
L + 2 (x + y) ≤ 108
a) Va reuși să treacă un pachet care măsoară 6 inci lățime, 8 inci înălțime și 5 picioare lungime??
b) Ce zici de unul care măsoară 2 x 2 x 4 picioare3?
c) Care este cea mai înaltă înălțime acceptabilă pentru un pachet a cărui bază este pătrată și măsoară 9 x 9 țoliDouă?
Raspunde la
L = 5 picioare = 60 inci
x = 6 inci
y = 8 inci
Operațiunea de rezolvat este:
L + 2 (x + y) = 60 + 2 (6 + 8) țoli = 60 + 2 x 14 țoli = 60 + 28 țoli = 88 țoli
Pachetul este acceptat.
Răspuns b
Dimensiunile acestui pachet sunt mai mici decât pachetul a), astfel încât ambii reușesc să treacă.
Răspundeți c
În acest pachet:
x = L = 9 țoli
Trebuie să se îndeplinească faptul că:
9+ 2 (9 + y) ≤ 108
27 + 2y ≤ 108
2y ≤ 81
și ≤ 40,5 țoli
Referințe
- Carena, M. 2019. Manual pre-universitar de matematică. Universitatea Națională a Litoralului.
- Diego, A. Numere reale și proprietățile lor. Recuperat de la: matematica.uns.edu.ar.
- Figuera, J. 2000. Matematica a 9-a. Grad. Ediții CO-BO.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Precalcul: Matematică pentru calcul. Al 5-lea. Ediție. Cengage Learning.



Nimeni nu a comentat acest articol încă.