Numere transcendente care sunt acestea, formule, exemple, exerciții

numere transcendente sunt cele care nu pot fi obținute ca urmare a unei ecuații polinomiale. Opusul unui număr transcendent este a număr algebric, care sunt soluții ale unei ecuații polinomiale de tipul:

la_n Xⁿ + la_n-1 X^n-1 +… + A_Două X^Două + la₁ x + a₀ = 0

Unde coeficienții a_n, la_n-1,… la_Două, la₁, la₀ sunt numere raționale, numite coeficienții polinomului. Dacă un număr x este o soluție la ecuația anterioară, atunci acel număr nu este transcendent.

Vom analiza câteva numere și vom vedea dacă sunt sau nu transcendente:

a) 3 nu este transcendent deoarece este o soluție de x - 3 = 0.

b) -2 nu poate fi transcendent deoarece este o soluție de x + 2 = 0.

c) ⅓ este o soluție de 3x - 1 = 0

d) O soluție a ecuației x^Două - 2x + 1 = 0 este √2 -1, deci numărul prin definiție nu este transcendent.

e) Niciunul nu este √2 deoarece este rezultatul ecuației x^Două - 2 = 0. Patratarea √2 dă rezultatul 2, care scăzut din 2 este egal cu zero. Deci √2 este un număr irațional, dar nu este transcendent.

Indice articol

• 1 Ce sunt numerele transcendente?
  • 1.1 Numărul π
  • 1.2 Numărul e
• 2 Formule în care apare numărul transcendent π
  • 2.1 Perimetrul circumferinței
  • 2.2 Aria unui cerc
  • 2.3 Suprafața unei sfere
  • 2.4 Volumul sferei
• 3 Exerciții
  • 3.1 - Exercițiul 1
  • 3.2 - Exercițiul 2
• 4 Referințe

Ce sunt numerele transcendente?

Problema este că nu există o regulă generală pentru a le obține (mai târziu vom spune o cale), dar unele dintre cele mai faimoase sunt numărul pi si Numărul Neper, notat respectiv prin: π Da și.

Numărul π

Numarul π Apare natural observând că coeficientul matematic dintre perimetrul P al unui cerc și diametrul acestuia D, indiferent dacă este un cerc mic sau mare, dă întotdeauna același număr, numit pi:

π = P / D ≈ 3.14159 ...

Aceasta înseamnă că, dacă diametrul circumferinței este luat ca unitate de măsură, pentru toate acestea, mari sau mici, perimetrul va fi întotdeauna P = 3,14 ... = π, așa cum se poate vedea în animația din figura 2.

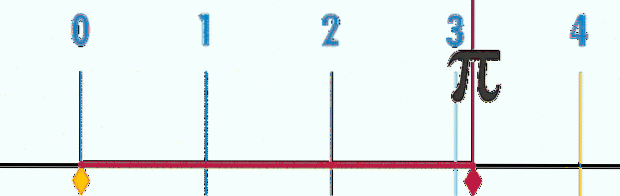
Pentru a determina mai multe zecimale, este necesar să se măsoare P și D cu o precizie mai mare și apoi să se calculeze coeficientul, care a fost făcut matematic. Concluzia este că zecimalele coeficientului nu au sfârșit și nu se repetă niciodată, deci numărul π pe lângă faptul că este transcendent, este și el iraţional.

Un număr irațional este un număr care nu poate fi exprimat ca împărțirea a două numere întregi. 

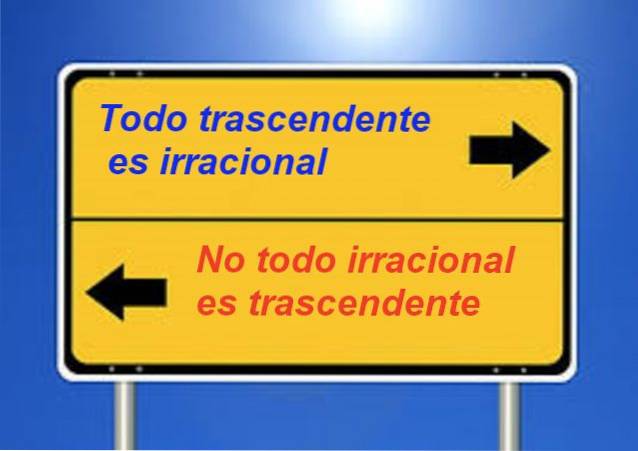
Se știe că fiecare număr transcendent este irațional, dar nu este adevărat că toate numerele iraționale sunt transcendente. De exemplu, √2 este irațional, dar nu este transcendent.

Numărul e

Numărul transcendent e este baza logaritmilor naturali și aproximarea sa zecimală este:

e ≈ 2.718281828459045235360 ... .

Dacă ai vrea să scrii numărul și exact, ar fi necesar să scriem zecimale infinite, deoarece fiecare număr transcendent este irațional, așa cum am spus mai înainte.

Primele zece cifre ale și sunt ușor de reținut:

2,7 1828 1828 și, deși pare să urmeze un model repetitiv, acest lucru nu se realizează în zecimale de ordin mai mare de nouă.

O definiție mai formală a și este următorul:

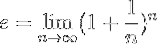
Ceea ce înseamnă că valoarea exactă a și se realizează prin efectuarea operației indicate în această formulă, când numărul natural n tinde spre infinit.

Acest lucru explică de ce putem obține doar aproximări ale și, deoarece oricât de mare ar fi numărul n, va fi întotdeauna posibil să găsim un n superior.

Să căutăm câteva aproximări pe cont propriu:

-Când n = 100 atunci (1 + 1/100)¹⁰⁰ = 2.70481 care greu coincide în prima zecimală cu valoarea „adevărată” a lui e.

-Dacă alegeți n = 10.000 aveți (1 + 1 / 10.000)^10.000 = 2.71815 care se potrivește cu valoarea „exactă” a lui în primele trei zecimale.

Acest proces ar trebui urmat la infinit pentru a obține valoarea „adevărată” a lui e. Nu cred că avem timp să o facem, dar să încercăm încă una:

Să folosim n = 100.000:

(1 + 1 / 100.000)^100.000 = 2,7182682372

Aceasta are doar patru zecimale care se potrivesc cu valoarea considerată exactă.

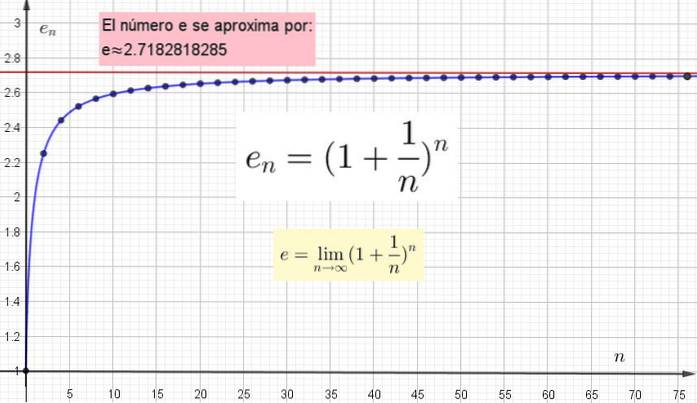
Important este să înțelegem că cu cât este mai mare valoarea lui n aleasă pentru a calcula e_n, cu cât este mai aproape de adevărata valoare. Dar acea valoare adevărată va avea doar atunci când n este infinit.

Alte numere importante

În afară de aceste numere celebre, există și alte numere transcendente, de exemplu:

- Două^√2

Fiecare număr algebric, altul decât 0 sau 1, ridicat la un exponent irațional va fi un număr transcendent.

-Numărul Champernowne din baza 10: 

C_10 = 0.123456789101112131415161718192021 ... .

-Numărul Champernowne din baza 2:

C_2 = 0.1101110010110111 ... .

-Numărul gamma γ sau constanta Euler-Mascheroni:

γ ≈ 0,577 215 664 901 532 860 606

Ceea ce se obține făcând următorul calcul:

γ ≈ 1 + ½ + ⅓ + ¼ +… + 1 / n - ln (n)

Cand n fii foarte foarte mare. Pentru a avea valoarea exactă a numărului Gamma, ar trebui să faceți calculul cu n infinit. Ceva similar cu ceea ce am făcut mai sus.

Și există mult mai multe numere transcendente. Marele matematician Georg Cantor, născut în Rusia și care a trăit între 1845 și 1918, a arătat că setul de numere transcendente este mult mai mare decât setul de numere algebrice.

Formule în care apare numărul transcendent π

Perimetrul circumferinței

P = π D = 2 π R, unde P este perimetrul, D diametrul și R raza circumferinței. Trebuie amintit că:

-Diametrul circumferinței este cel mai lung segment care unește două puncte ale aceleiași și care trece întotdeauna prin centrul său,

-Raza este jumătate din diametru și este segmentul care merge de la centru la margine.

Zona unui cerc

A = π R^Două = ¼ π D^Două

Suprafața unei sfere

S = 4 π R^Două.

Da. Deși s-ar putea să nu pară, suprafața unei sfere este aceeași cu cea a patru cercuri cu aceeași rază ca sfera..

Volumul sferei

V = 4/3 π R³

Instruire

- Exercitiul 1

Pizzeria „EXÓTICA” vinde pizza de trei diametre: 30 cm mici, 37 cm mijlocii și 45 cm mari. Un copil este foarte flămând și și-a dat seama că două pizza mici costă la fel ca una mare. Ce va fi mai bun pentru el, cumpără două pizza mici sau una mare?

Soluţie

Cu cât suprafața este mai mare, cu atât este mai mare cantitatea de pizza, din acest motiv, suprafața unei pizza mari va fi calculată și comparată cu cea a două pizza mici:

Zona mare de pizza = ¼ π D^Două = ¼ .13.1416⋅45^Două = 1590,44 cm^Două

Mică zonă de pizza = ¼ π d^Două = ¼ ⋅3.1416⋅30^Două = 706,86 cm^Două

Prin urmare, două pizza mici vor avea o suprafață de 

2 x 706,86 = 1413,72 cm^Două .

Este clar: veți avea mai multă pizza cumpărând o singură mare decât două mici.

- Exercițiul 2

Pizzeria „EXÓTICA” vinde și o pizza emisferică cu o rază de 30 cm la același preț ca una de formă dreptunghiulară cu o latură de 30 x 40 cm. Pe care ai alege-o?

Soluţie

După cum sa menționat în secțiunea anterioară, suprafața unei sfere este de patru ori mai mare decât cea a unui cerc cu același diametru, deci o emisferă de 30 cm în diametru va avea:

Pizza emisferică de 12 ": 1413,72 cm^Două (de două ori circulară cu același diametru)

Pizza dreptunghiulară: (30 cm) x (40 cm) = 1200 cm^Două .

Pizza emisferică are o suprafață mai mare.

Referințe

1. Fernández J. Numărul e. Originea și curiozitățile. Recuperat de pe: soymatematicas.com
2. Bucurați-vă de matematică. Numărul lui Euler. Recuperat de pe: gustolasmatematicas.com.
3. Figuera, J. 2000. Matematica 1. Diversificat. Ediții CO-BO.
4. García, M. Numărul e din calculul elementar. Recuperat de la: matematica.ciens.ucv.ve.
5. Wikipedia. Numărul PI. Recuperat de pe: wikipedia.com
6. Wikipedia. Numere transcendente. Recuperat de pe: wikipedia.com