Definiție paraboloidă hiperbolică, proprietăți și exemple

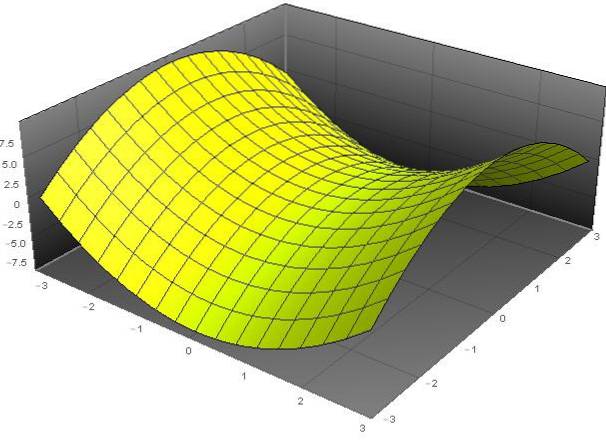
A paraboloid hiperbolic este o suprafață a cărei ecuație generală în coordonate carteziene (x, y, z) îndeplinește următoarea ecuație:

(pentru)^Două - (și / b)^Două - z = 0.

Denumirea de "paraboloid" provine din faptul că variabila z depinde de pătratele variabilelor x și y. În timp ce adjectivul „hiperbolic” se datorează faptului că la valori fixe ale lui z avem ecuația unei hiperbole. Forma acestei suprafețe este similară cu cea a unei șei de cai.

Indice articol

• 1 Descrierea paraboloidului hiperbolic
• 2 Proprietățile paraboloidului hiperbolic
• 3 Exemple lucrate
  • 3.1 - Exemplul 1
  • 3.2 - Exemplul 2
  • 3.3 - Exemplul 3
• 4 Paraboloidul hiperbolic în arhitectură
• 5 Referințe

Descrierea paraboloidului hiperbolic

Pentru a înțelege natura paraboloidului hiperbolic, se va face următoarea analiză:

1.- Vom lua cazul particular a = 1, b = 1, adică ecuația carteziană a paraboloidului rămâne z = x^Două - Da^Două.

2.- Se consideră planuri paralele cu planul ZX, adică y = ctte.

3.- Cu y = ctte rămâne z = x^Două - C, care reprezintă parabole cu ramuri în sus și vârf sub planul XY.

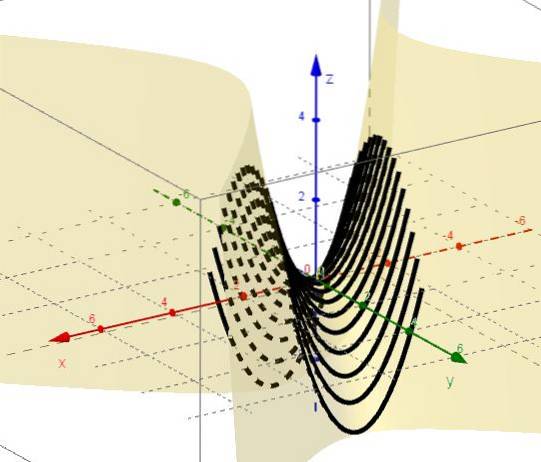
4.- Cu x = ctte rămâne z = C - y^Două, care reprezintă parabole cu ramuri în jos și vârf deasupra planului XY.

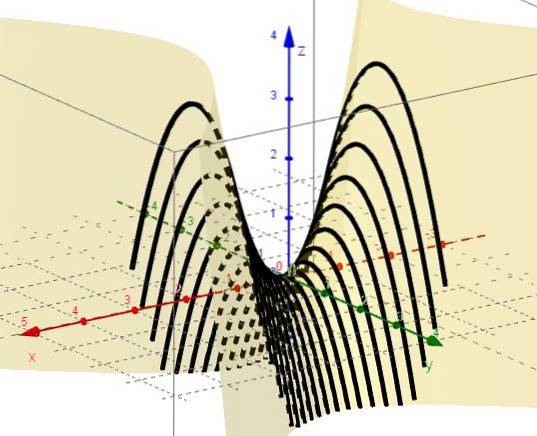
5.- Cu z = ctte rămâne C = x^Două - Da^Două, care reprezintă hiperboli în planuri paralele cu planul XY. Când C = 0 există două linii (la + 45º și -45º în raport cu axa X) care se intersectează la origine pe planul XY.

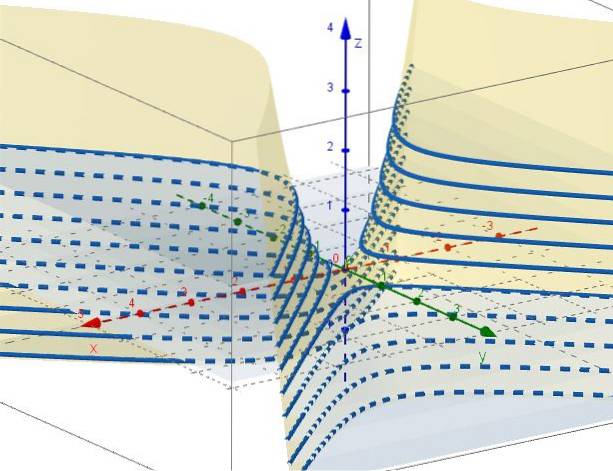
Proprietățile paraboloidului hiperbolic

1.- Patru puncte diferite în spațiul tridimensional definesc un singur paraboloid hiperbolic.

2.- Paraboloidul hiperbolic este un suprafață dublu guvernată. Aceasta înseamnă că, în ciuda faptului că este o suprafață curbată, două linii diferite trec prin fiecare punct al unui paraboloid hiperbolic care aparține în totalitate paraboloidului hiperbolic. Cealaltă suprafață care nu este un plan și este dublat condusă este hiperboloid al revoluției.

Tocmai a doua proprietate a paraboloidului hiperbolic a permis utilizarea sa largă în arhitectură, deoarece suprafața poate fi generată din grinzi sau corzi drepte..

A doua proprietate a paraboloidului hiperbolic permite o definiție alternativă a acestuia: este suprafața care poate fi generată de o linie dreaptă în mișcare paralelă cu un plan fix și care taie două linii fixe care servesc drept ghid. Următoarea figură clarifică această definiție alternativă a paraboloidului hiperbolic:

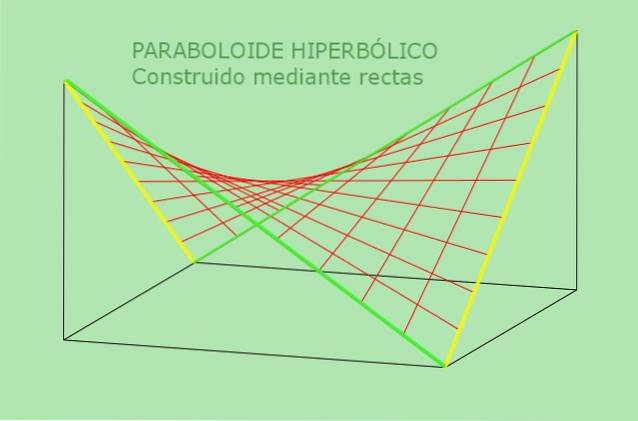
Exemple lucrate

- Exemplul 1

Arată că ecuația: z = xy, corespunde unui paraboloid hiperbolic.

Soluţie

O transformare va fi aplicată variabilelor x și y corespunzătoare unei rotații a axelor carteziene față de axa Z de + 45º. Vechile coordonate x și y sunt transformate în noile x și y în conformitate cu următoarele relații:

x = x '- y'

y = x '+ y'

în timp ce coordonata z rămâne aceeași, adică z = z '.

Înlocuind în ecuația z = x și avem:

z '= (x' - y ') (x' + y ')

Prin aplicarea produsului notabil al diferenței cu suma egală cu diferența de pătrate, avem:

z '= x'^Două - Y '^Două

care corespunde în mod clar definiției date inițial de paraboloid hiperbolic.

Intercepția planurilor paralele cu axa XY cu paraboloidul hiperbolic z = x și determină hiperbolele echilaterale care au ca asimptote planurile x = 0 și y = 0.

- Exemplul 2

Determinați parametrii la Da b a paraboloidului hiperbolic care trece prin punctele A (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) și D (2, -1, 32/9).

Soluţie

Conform proprietăților sale, patru puncte din spațiul tridimensional determină un singur paraboloid hiperbolic. Ecuația generală este:

z = (x / a)^Două - (și / b)^Două

Înlocuim valorile date:

Pentru punctul A avem 0 = (0 / a)^Două - (0 / b)^Două, ecuație care este satisfăcută indiferent de valorile parametrilor a și b.

Înlocuind punctul B, obținem:

5/9 = 1 / a^Două - 1 B^Două

În timp ce pentru punctul C rămâne:

32/9 = 4 / a^Două - 1 B^Două

În cele din urmă, pentru punctul D obținem:

32/9 = 4 / a^Două - 1 B^Două

Care este identic cu ecuația anterioară. În cele din urmă, sistemul de ecuații trebuie rezolvat:

5/9 = 1 / a^Două - 1 B^Două

32/9 = 4 / a^Două - 1 B^Două

Scăderea celei de-a doua ecuații din prima dă:

27/9 = 3 / a^Două ceea ce implică faptul că a^Două = 1.

În mod similar, a doua ecuație se scade din cvadruplul primei, obținând:

(32-20) / 9 = 4 / a^Două - 4 / a^Două -1 B^Două + 4 / b^Două

Care este simplificat ca:

12/9 = 3 / b^Două ⇒ b^Două = 9/4.

Pe scurt, paraboloidul hiperbolic care trece prin punctele date A, B, C și D are o ecuație cartesiană dată de:

z = x^Două - (4/9) și^Două

- Exemplul 3

Conform proprietăților paraboloidului hiperbolic, două linii trec prin fiecare punct care este complet conținut în el. Pentru cazul z = x ^ 2 - y ^ 2 găsiți ecuația celor două linii care trec prin punctul P (0, 1, -1) aparținând în mod clar paraboloidului hiperbolic, astfel încât toate punctele acestor linii să aparțină și ele la fel.

Soluţie

Folosind produsul remarcabil al diferenței de pătrate, ecuația pentru paraboloidul hiperbolic poate fi scrisă astfel:

(x + y) (x - y) = c z (1 / c)

Unde c este o constantă diferită de zero.

Ecuația x + y = c z, și ecuația x - y = 1 / c corespund a două planuri cu vectori normali n=<1,1,-c> Da m=<1,-1,0>. Produsul vector m x n =<-c, -c, -2> ne dă direcția liniei de intersecție a celor două planuri. Atunci una dintre liniile care trece prin punctul P și aparține paraboloidului hiperbolic are o ecuație parametrică:

= <0, 1, -1> + t <-c, -c, -2>

Pentru a determina c substituim punctul P din ecuația x + y = c z, obținând:

c = -1

În mod similar, dar având în vedere ecuațiile (x - y = k z) și (x + y = 1 / k) avem ecuația parametrică a liniei:

= <0, 1, -1> + s cu k = 1.

Pe scurt, cele două linii:

= <0, 1, -1> + t <1, 1, -2> Da  = <0, 1, -1> + s <1, -1, 2>

Ele sunt complet conținute în paraboloidul hiperbolic z = x^Două - Da^Două care trece prin punctul (0, 1, -1).

Ca o verificare, să presupunem t = 1 care ne dă punctul (1,2, -3) pe prima linie. Trebuie să verificați dacă este și pe paraboloidul z = x^Două - Da^Două:

-3 = 1^Două - Două^Două = 1 - 4 = -3

Ceea ce confirmă faptul că aparține într-adevăr suprafeței paraboloidului hiperbolic.

Paraboloidul hiperbolic din arhitectură

Paraboloidul hiperbolic a fost folosit în arhitectură de marii arhitecți de avangardă, printre care se remarcă numele arhitectului spaniol Antoni Gaudí (1852-1926) și, în special, și al spaniolului Félix Candela (1910-1997)..

Mai jos sunt câteva lucrări bazate pe paraboloidul hiperbolic:

-Capela orașului Cuernavaca (Mexic) operă a arhitectului Félix Candela.

-The Oceanographic of Valencia (Spania), tot de Félix Candela.

Referințe

1. Enciclopedia matematicii. Suprafață guvernată. Recuperat de pe: encyclopediaofmath.org
2. Llera Rubén. Paraboloid hiperbolic. Recuperat de pe: rubenllera.wordpress.com
3. Weisstein, Eric W. „Paraboloid hiperbolic”. Din MathWorld-A Wolfram Web Resource. Recuperat de pe: mathworld.wolfram.com
4. Wikipedia. Paraboloid. Recuperat de pe: en.wikipedia.com
5. Wikipedia. Paraboloid. Recuperat de pe: es.wikipedia.com
6. Wikipedia. Suprafața guvernată. Recuperat de pe: en.wikipedia.com