
Panta unei formule de linie și ecuații, reprezentare, exemple
panta unei linii este tangenta unghiului θ pe care linia respectivă îl formează cu axa orizontală, care prin convenție se măsoară în sens invers acelor de ceasornic. Panta oricărei linii este întotdeauna constantă și de aceea este una dintre cele mai esențiale caracteristici ale sale..
Pentru a o calcula, trebuie să cunoașteți două puncte pe linie, ale căror coordonate sunt (x1,Da1) și (xDouă,DaDouă). Un segment care aparține liniei este trasat între ambele puncte și apoi sunt trasate segmentele care reprezintă distanța dintre x.1 și xDouă, și între și1 si siDouă, ca în figura de mai jos.
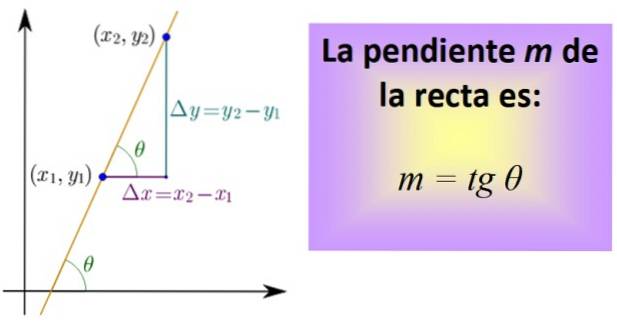
Cele trei segmente alcătuiesc un triunghi dreptunghi al cărui picioare sunt: Δx = xDouă - X1 y Δy = yDouă - Da1. Ele corespund respectiv unei deplasări orizontale și verticale..
Acum definim un coeficient, numit tangenta unghiului θ și abreviat tg θ, care este exact panta m a dreptului:
m = tg θ = Δy / Δx
Rețineți că pentru o linie, acest unghi rămâne constant, indiferent de punctele luate pentru calcularea tangentei sale. În orice caz, această valoare ne oferă o măsură a cât de abruptă este linia.
Prin coordonatele punctelor selectate, formula pentru pantă este:
m = (y - y1 ) / (XDouă - X1)
Indice articol
- 1 Reprezentare grafică
- 2 Tipuri de panta
- 3 Cum calculați panta unei linii?
- 4 exerciții rezolvate
- 4.1 - Exercițiul 1
- 4.2 - Exercițiul 2
- 5 Exemple
- 5.1 Exemplul 1
- 5.2 Exemplul 2
- 6 Referințe
Reprezentare grafică
Mai jos avem mai multe situații în care conceptul de pantă este relevant. Valoarea sa poate fi calculată cu ușurință prin măsurarea deplasării verticale și orizontale respective și apoi realizând coeficientul indicat la început.
Acest lucru ne dă o idee despre denivelările sau declinul unei structuri, cum ar fi o rampă, un acoperiș sau un drum:
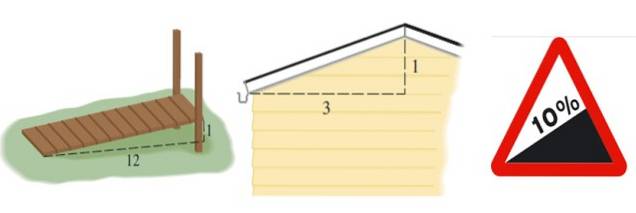
Panta rampei prezentată în figura 2 din stânga este m = 1/12, cea a acoperișului este m = 1/3 și cea a drumului este exprimată în procente. Un procent de 10% înseamnă că pentru fiecare 100 de metri care avansează orizontal se câștigă 10 metri în înălțime:
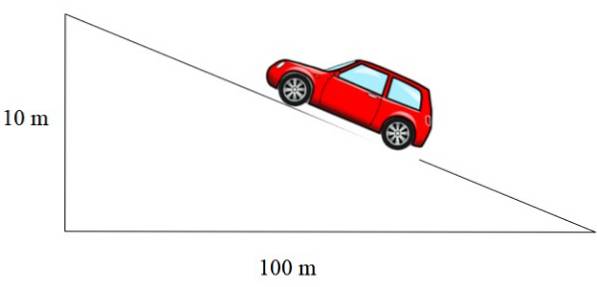
În acest caz, panta este 10/100 = 0,1, care, exprimată procentual, este egală cu 10%..
Tipuri de pante
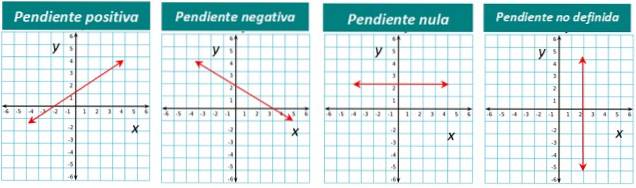
Panta unei linii poate fi pozitivă, negativă sau zero. De exemplu, linia prezentată în figura 1 are o pantă pozitivă. O apreciem imediat pentru că vedem că linia „crește” dacă o vedem de la stânga la dreapta.
Dacă linia coboară de la stânga la dreapta, atunci panta ei este negativă. Și când o linie este orizontală, panta ei este zero.
În cele din urmă, pentru liniile verticale, panta nu este definită.
Reprezentarea grafică a fiecărui tip este mai jos:
Cum calculați panta unei linii?
Calculul pantei este foarte simplu, trebuie doar să găsiți deplasarea verticală și deplasarea orizontală, apoi să faceți coeficientul dintre ambele.
Când avem desenul liniei în plan cartezian, aceste deplasări se găsesc alegând două puncte pe dreapta P1 Și pDouă, determinarea coordonatelor sale și aplicarea definiției date la început:
m = (y - y1 ) / (XDouă - X1 )
Deoarece valoarea pantei este independentă de alegerea lui P1 Și pDouă , vom alege un punct P oricare dintre coordonatele (x, y) care aparține liniei, ale cărei coordonate nu sunt cunoscute și un alt punct P1 ale căror coordonate sunt: (x1,Da1).
Panta este:
m = (y - y1) / (x - x1)
Putem elimina Da:
si si1 = m (x - x1)
Acum presupunem că punctul P1 este intersecția liniei cu axa verticală, a coordonatelor (0, b). Înlocuind acest lucru în ecuația de mai sus:
y - b = m (x - 0) → y = mx + b
Această expresie este cunoscută sub numele de ecuația liniei din formă panta - interceptare, întrucât linia este determinată fără echivoc atunci când se cunosc panta și intersecția sa cu axa verticală.
Cunoașterea numai a pantei nu este suficientă pentru a caracteriza o linie pe plan, deoarece liniile infinite ar putea avea aceeași pantă, ceea ce înseamnă că sunt paralele, dar trec prin alte puncte.
Exerciții rezolvate
- Exercitiul 1
Găsiți panta liniei prezentate în figura următoare:
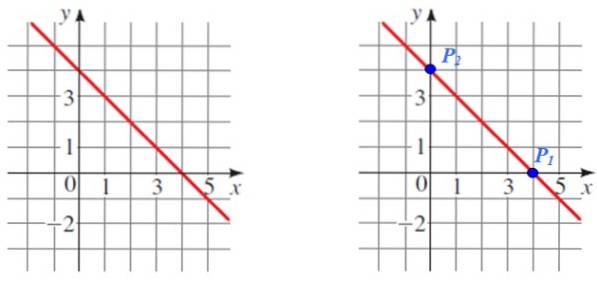
Soluţie
P1 Și pDouă sunt două puncte ușor de citit care vor fi utilizate pentru calcul, rețineți, de asemenea, că sunt intersecțiile respective cu axele de coordonate.
Coordonatele fiecărui punct sunt:
P1 (4.0) și PDouă (0,4)
Înlocuind în ecuație panta:
m = (4 - 0) / (0 - 4) = 4 / (- 4) = -1
Panta este negativă, ceea ce era de așteptat după ce am analizat graficul.
- Exercițiul 2
Găsiți ecuația liniei care trece prin punctul (1, -6) și este paralelă cu linia y = 2x - 3.
Soluţie
Panta liniei căutate trebuie să fie aceeași cu cea a lui y = 2x - 3, deoarece acestea sunt paralele. Pentru această linie panta este m = 2, deci cea pe care o căutăm are forma:
si si1 = 2 (x - x1)
Acum înlocuim punctul prin care trece linia noastră: x1 = 1 și y1 = -6.
y - (-6) = 2 (x - 1)
Prin urmare y = 2x - 2 - 6 → y = 2x - 8
Exemple
Două cantități pot fi corelate în așa fel încât graficul lor să fie o linie dreaptă. În acest caz, se spune că mărimile au dependență liniară și panta liniei poate fi interpretată ca rata de schimbare de la o variabilă la alta.
Exemplul 1
Să presupunem că o piscină este umplută cu apă la a rată constantă în timp. Firește, cu cât trece mai mult timp, cu atât este stocată mai multă apă. Ei bine, rata la care este umplută piscina este tocmai panta liniei care leagă volumul de timp:
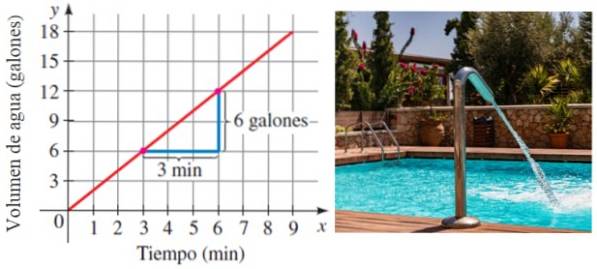
În acest exemplu, piscina se umple cu o rată de 6/3 galoane pe minut sau 2 galoane / minut.
Exemplul 2
Când un mobil se deplasează în linie dreaptă cu viteză constantă, panta graficului de poziție în funcție de timp nu este alta decât viteza menționată. Graficul arată un mobil cu viteză pozitivă, ceea ce înseamnă că se îndepărtează de origine.
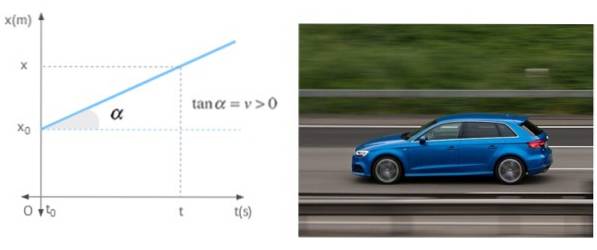
Referințe
- Alvarez, J. Panta unei autostrăzi. Recuperat de pe: geogebra.es.
- Carena, M. 2019. Manual pre-universitar de matematică. Universitatea Națională a Litoralului.
- Hoffman, J. Selecția subiectelor de matematică. Volumul 4.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Precalcul: Matematică pentru calcul. Al 5-lea. Ediție. Cengage Learning.
- Zill, D. 1984. Algebră și trigonometrie. Dealul Mcgraw.


Nimeni nu a comentat acest articol încă.