
Care este echilibrul particulei? (Cu exemple)
echilibrul particulelor Este o stare în care o particulă se găsește atunci când forțele externe care acționează asupra lor sunt anulate reciproc. Aceasta presupune că menține o stare constantă, astfel încât să poată apărea în două moduri diferite, în funcție de situația specifică.
Primul este să fii în echilibru static, în care particula este imobilă; iar al doilea este echilibrul dinamic, în care sumarea forțelor se anulează, dar totuși particula are o mișcare rectilinie uniformă.

Modelul de particule este o aproximare foarte utilă pentru a studia mișcarea unui corp. Acesta constă în presupunerea că toată masa corpului este concentrată într-un singur punct, indiferent de mărimea obiectului. În acest fel puteți reprezenta o planetă, o mașină, un electron sau o bilă de biliard.
Indice articol
- 1 Forța rezultată
- 2 diagrame cu corp liber
- 3 Moduri de aplicare a condiției de echilibru
- 3.1 Două forțe de aceeași magnitudine și direcție și direcții opuse
- 3.2 Două forțe de magnitudine diferită, aceeași direcție și direcții opuse
- 3.3 Două forțe de aceeași magnitudine și direcție diferită
- 3.4 Trei forțe cu direcție diferită
- 4 frecare
- 4.1 Fricțiunea dinamică
- 5 Exemplu lucrat
- 5.1 Soluție
- 6 Referințe
Forța rezultată
Punctul care reprezintă obiectul este locul în care acționează forțele care îl afectează. Toate aceste forțe pot fi înlocuite cu una singură care face același efect, care se numește forță rezultantă sau forta neta și este notat ca FR sau FN.
Conform celei de-a doua legi a lui Newton, atunci când există o forță rezultantă dezechilibrată, corpul experimentează o accelerație proporțională cu forța:
FR = m.a
Unde la este accelerația pe care obiectul o dobândește grație acțiunii forței și m este masa obiectului. Ce se întâmplă dacă corpul nu este accelerat? Tocmai ceea ce a fost indicat la început: corpul este în repaus sau se mișcă cu mișcare rectilinie uniformă, care nu are accelerație.
Pentru o particulă în echilibru este valabil să se asigure că:
FR = 0
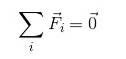
Deoarece adăugarea vectorilor nu implică neapărat adăugarea modulelor, vectorii trebuie descompuși. Astfel, este valabil să se exprime:
FX = m.aX = 0; FDa = m.aDa = 0; Fz = m.az = 0
Diagrame cu corp liber
Pentru a vizualiza forțele care acționează asupra particulei, este convenabil să faceți o diagramă a corpului liber, în care toate forțele care acționează asupra obiectului sunt reprezentate de săgeți..
Ecuațiile de mai sus sunt de natură vectorială. La descompunerea forțelor, acestea se disting prin semne. În acest fel este posibil ca suma componentelor sale să fie zero.
Următoarele sunt linii directoare importante pentru a face desenul util:
- Alegeți un sistem de referință în care cea mai mare cantitate de forțe se află pe axele de coordonate.
- Greutatea este întotdeauna trasă vertical în jos.
- În cazul a două sau mai multe suprafețe în contact, există forțe normale, care sunt întotdeauna trase prin împingerea corpului și perpendiculare pe suprafața care îl exercită..
- Pentru o particulă în echilibru pot exista fricțiuni paralele cu suprafața de contact și opuse mișcării posibile, dacă particula este considerată în repaus sau definitiv în opoziție, dacă particula se mișcă cu MRU (mișcare rectilinie uniformă).
- Dacă există o frânghie, tensiunea este întotdeauna trasă de-a lungul ei și trăgând corpul.
Modalități de aplicare a condiției de echilibru
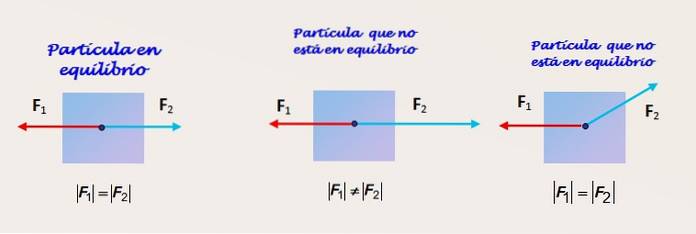
Două forțe de aceeași magnitudine și direcție și direcții opuse
Figura 2 prezintă o particulă asupra căreia acționează două forțe. În figura din stânga particula primește acțiunea a două forțe F1 și FDouă care au aceeași magnitudine și acționează în aceeași direcție și în direcții opuse.
Particula este în echilibru, dar totuși, cu informațiile furnizate, nu este posibil să se știe dacă echilibrul este static sau dinamic. Sunt necesare mai multe informații despre cadrul de referință inerțial din care este observat obiectul.
Două forțe de magnitudine diferită, aceeași direcție și direcții opuse
Figura din centru arată aceeași particulă, care de data aceasta nu este în echilibru, deoarece magnitudinea forței FDouă este mai mare decât cea a lui F1. Prin urmare, există o forță dezechilibrată și obiectul are o accelerație în aceeași direcție ca FDouă.
Două forțe de aceeași magnitudine și direcție diferită
În cele din urmă, în figura din dreapta vedem un corp care nu este nici în echilibru. În ciuda faptului că F1 și FDouă au magnitudine egală, forța FDouă nu este în aceeași direcție ca 1. Componenta verticală a lui FDouă nu este contracarat de niciun altul și particula are o accelerare în acea direcție.
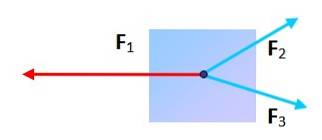
Trei forțe cu direcție diferită
O particulă supusă a trei forțe poate fi în echilibru? Da, atâta timp cât atunci când plasați capătul și sfârșitul fiecăruia, figura rezultată este un triunghi. În acest caz, suma vectorială este zero.
Frecare
O forță care intervine frecvent în echilibrul particulei este frecarea statică. Se datorează interacțiunii obiectului reprezentat de particulă cu suprafața altuia. De exemplu, o carte în echilibru static pe o masă înclinată este modelată ca o particulă și are o diagramă cu corp liber, după cum urmează:
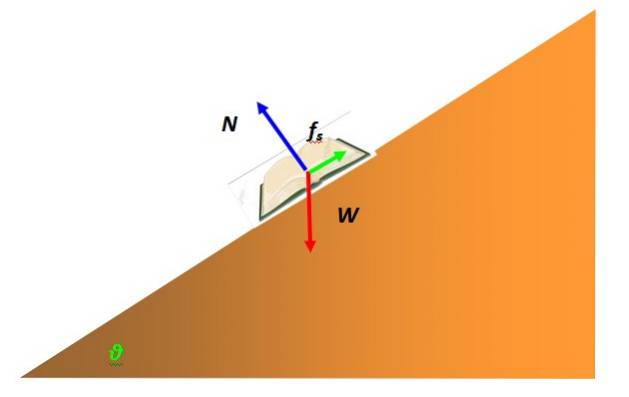
Forța care împiedică cartea să alunece pe suprafața planului înclinat și să rămână în repaus este frecare statică. Depinde de natura suprafețelor în contact, care prezintă microscopic asperități cu vârfuri care se întrepătrund, făcând mișcarea dificilă..
Valoarea maximă a fricțiunii statice este proporțională cu forța normală, forța exercitată de suprafață asupra obiectului susținut, dar perpendicular pe suprafața menționată. În exemplul din carte este indicat cu albastru. Matematic se exprimă astfel:
Fs mai mult∝ N
Constanta proporționalității este coeficient de frecare static μs, care este determinat experimental, este adimensional și depinde de natura suprafețelor în contact.
Fs max = μs N
Fricțiunea dinamică
Dacă o particulă se află în echilibru dinamic, mișcarea are loc deja și nu mai intervine fricțiunea statică. Dacă este prezentă vreo forță de frecare care se opune mișcării, acționează fricțiunea dinamică, a cărei magnitudine este constantă și este dată de:
Fk = μk N
Unde μk este el coeficientul de frecare dinamic, Depinde și de tipul de suprafețe în contact. La fel ca și coeficientul de frecare static, este adimensional și valoarea sa este determinată experimental.
Valoarea coeficientului de frecare dinamică este de obicei mai mică decât cea a fricțiunii statice.
Exemplu lucrat
Cartea din Figura 3 este în repaus și are o masă de 1,30 kg. Planul are un unghi de înclinare de 30º. Găsiți coeficientul de frecare statică dintre carte și suprafața plană.
Soluţie
Este important să selectați un sistem de referință adecvat, a se vedea următoarea figură:
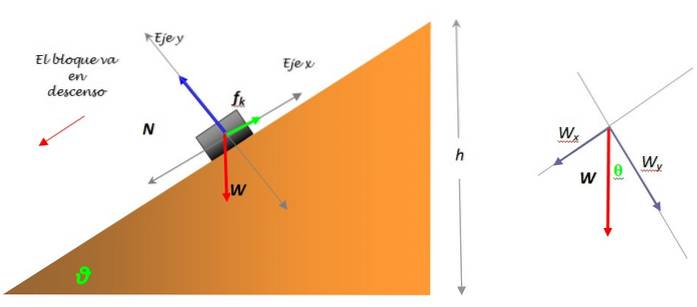
Greutatea cărții are magnitudine L = mg, cu toate acestea, este necesar să îl împărțim în două componente: WX Da WDa, întrucât este singura forță care nu cade chiar deasupra oricărei axe de coordonate. Descompunerea greutății este observată în figura din stânga.
WDa = mg.cosθ = 1,30 x 9,8 x cos 30º N = 11,03 N
WX = mg sinθ = 1,30 x 9,8 x sin 30º = 6,37 N
Al 2-lea. Legea lui Newton pentru axa verticală este:
N - Wy = 0
N = mg. cos θ = 11,03 N.
Aplicând al doilea. Legea lui Newton pentru axa x, alegând direcția mișcării posibile ca pozitivă:
WX - Fs = 0
Fricțiunea maximă este Fs max= μsN, Prin urmare:
WX - μsN = 0
μs = WX / N = 6,37 / 11,03 = 0,58
Referințe
- Rex, A. 2011. Fundamentele fizicii. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7ma. Ed. Cengage Learning. 120 - 124.
- Serway, R., Vulle, C. 2011. Fundamentele fizicii. 9n / A Ed. Cengage Learning. 99-112.
- Tippens, P. 2011. Fizică: concepte și aplicații. Ediția a VII-a. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Fizică. Addison Wesley. 148-164.



Nimeni nu a comentat acest articol încă.