
Ce este rangul în statistici? (Cu exemple)
rang, distanța sau amplitudinea, în statistici, este diferența (scăderea) dintre valoarea maximă și valoarea minimă a unui set de date dintr-un eșantion sau dintr-o populație. Dacă intervalul este reprezentat de litera R și datele de X, formula pentru interval este pur și simplu:
R = xmax - Xmin
Unde xmax este valoarea maximă a datelor și xmin este minimul.
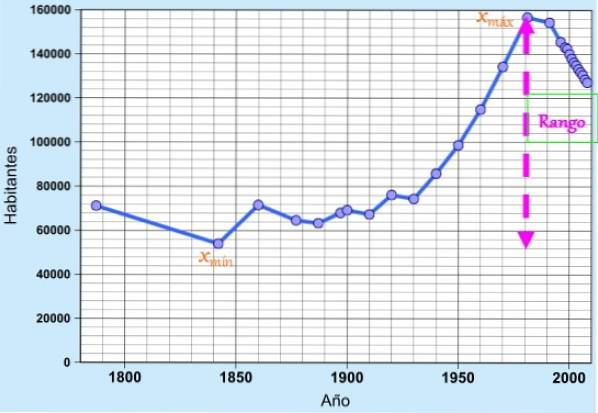
Conceptul este foarte util ca o simplă măsură a dispersiei pentru a aprecia rapid variabilitatea datelor, deoarece indică extensia sau lungimea intervalului în care acestea sunt găsite..
De exemplu, să presupunem că se măsoară înălțimea unui grup de 25 de bărbați studenți din ingineria primului an la o universitate. Cel mai înalt elev din grupă are 1,93 m, iar cel mai scurt 1,67 m. Acestea sunt valorile extreme ale datelor eșantionului, prin urmare calea lor este:
R = 1,93 - 1,67 m = 0,26 m sau 26 cm.
Înălțimea elevilor din acest grup este distribuită de-a lungul acestui interval.
Indice articol
- 1 Avantaje și dezavantaje
- 1.1 Dezavantaje ale intervalului ca măsură a dispersiei
- 2 Gama interquartile, quartile și exemplul lucrat
- 2.1 - Calculul quartilelor
- 3 Exemplu lucrat
- 4 Referințe
Avantaje și dezavantaje
Gama este, așa cum am spus mai înainte, o măsură a cât de răspândite sunt datele. Un interval mic indică faptul că datele sunt mai mult sau mai puțin apropiate și că există o răspândire mică. Pe de altă parte, o gamă mai largă indică faptul că datele sunt mai dispersate..
Avantajele calculării intervalului sunt evidente: este foarte simplu și rapid de găsit, deoarece este o simplă diferență.
De asemenea, are aceleași unități ca datele cu care funcționează, iar conceptul este foarte ușor de interpretat pentru orice observator..
În exemplul înălțimii studenților ingineri, dacă domeniul ar fi fost de 5 cm, am spune că studenții au toți aproximativ aceeași dimensiune. Dar cu o rază de acțiune de 26 cm, presupunem imediat că există probe de toate înălțimile intermediare în eșantion. Este această presupunere întotdeauna corectă?
Dezavantajele intervalului ca măsură a dispersiei
Dacă ne uităm cu atenție, este posibil ca în eșantionul nostru de 25 de studenți ingineri, doar unul dintre ei să măsoare 1,93 și restul de 24 să aibă înălțimi de aproape 1,67 m.
Și totuși, raza de acțiune rămâne aceeași, deși opusul este perfect posibil: că înălțimea majorității este de aproximativ 1,90 m și doar una este de 1,67 m.
În ambele cazuri, distribuția datelor este destul de diferită.
Dezavantajele intervalului ca măsură a dispersiei se datorează faptului că folosește doar valori extreme și le ignoră pe toate celelalte. Deoarece majoritatea informațiilor sunt pierdute, nu aveți nicio idee despre cum sunt distribuite datele eșantionului.
O altă caracteristică importantă este că intervalul probei nu scade niciodată. Dacă adăugăm mai multe informații, adică luăm în considerare mai multe date, intervalul crește sau rămâne același.
Și în orice caz, este util numai atunci când se lucrează cu probe mici, singura sa utilizare ca măsură de dispersie în probe mari nu este recomandată..
Ce trebuie să faceți este să completați cu calculul altor măsuri de dispersie care iau în considerare informațiile furnizate de datele totale: ruta interquartile, varianța, abaterea standard și coeficientul de variație.
Gama interquartile, quartile și exemplul lucrat
Ne-am dat seama că slăbiciunea intervalului ca măsură a dispersiei este că folosește doar valorile extreme ale distribuției datelor, omițându-le pe celelalte..
Pentru a evita acest inconvenient, quartile: trei valori cunoscute sub numele de măsurători de poziție.
Distribuie datele negroupate în patru părți (alte măsuri de poziție utilizate pe scară largă sunt decile si percentile). Acestea sunt caracteristicile sale:
-Primul quartile Q1 este valoarea datelor astfel încât 25% din toate acestea să fie mai mici decât Q1.
-Al doilea quartile QDouă este median din distribuție, ceea ce înseamnă că jumătate (50%) din date este mai mică decât acea valoare.
-În sfârșit, al treilea quartil Q3 subliniază că 75% din date sunt mai mici decât Q3.
Apoi, intervalul intercuartil sau domeniul intercuartil este definit ca diferența dintre al treilea quartil Q3 iar primul quartile Q1 a datelor:
Gama intercuartilă = RÎ = Î3 - Î1
În acest fel, valoarea intervalului RÎ nu este la fel de afectat de valori extreme. Din acest motiv, este recomandabil să-l utilizați atunci când aveți de-a face cu distribuții înclinate, cum ar fi cele ale elevilor foarte înalți sau foarte scurți descriși mai sus..
- Calculul quartilelor
Există mai multe modalități de a le calcula, aici vă vom propune una, dar în orice caz este necesar să cunoașteți numărul comenzii „Nsau”, Care este locul pe care îl ocupă quartila respectivă în distribuție.
Adică, dacă, de exemplu, termenul care corespunde lui Q1 este a doua, a treia sau a patra și așa mai departe din distribuție.
Prima quartilă
Nsau (Î1) = (N + 1) / 4
Al doilea quartil sau median
Nsau (ÎDouă) = (N + 1) / 2
Al treilea quartile
Nsau (Î3) = 3 (N + 1) / 4
Unde N este numărul de date.
Mediana este valoarea care se află chiar în mijlocul distribuției. Dacă numărul de date este impar, nu există nicio problemă în găsirea acestuia, dar dacă este par, atunci cele două valori centrale sunt calculate pentru a deveni una.
Odată calculat numărul comenzii, se respectă una dintre aceste trei reguli:
-Dacă nu are zecimale, datele indicate în distribuție sunt căutate și aceasta va fi quartila căutată.
-Când numărul comenzii este la jumătatea distanței dintre două, atunci datele indicate de partea întreagă sunt calculate cu următoarele date, iar rezultatul este quartila corespunzătoare.
-În orice alt caz, este rotunjit la cel mai apropiat număr întreg și aceasta va fi poziția quartilei.
Exemplu lucrat
Pe o scară de la 0 la 20, un grup de 16 studenți la matematică I au obținut următoarele note (puncte) la un examen intermediar:
16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14
Găsi:
a) Intervalul sau intervalul de date.
b) Valorile quartilelor Q1 și Q3
c) Gama intercuartilă.

Solutie la
Primul lucru de făcut pentru a găsi calea este să ordonați datele în ordine crescătoare sau descrescătoare. De exemplu, în ordine crescătoare aveți:
1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20
Folosind formula dată la început: R = xmax - Xmin
R = 20 - 1 puncte = 19 puncte.
Conform rezultatului, aceste calificări au o mare dispersie.
Soluția b
N = 16
Nsau (Î1) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4,25
Este un număr cu zecimale, a cărui parte întreagă este 4. Apoi mergem la distribuție, căutăm datele care ocupă locul al patrulea și valoarea sa este mediată cu cea a poziției a cincea. Deoarece ambii sunt 9, media este și 9 și așa:
Î1 = 9
Acum repetăm procedura pentru a găsi Q3:
Nsau (Î3) = 3 (N + 1) / 4 = 3 (16 +1) / 4 = 12,75
Din nou, este o zecimală, dar, deoarece nu este la jumătatea drumului, este rotunjită la 13. Cuartila pe care o căutăm ocupă poziția a treisprezecea și este:
Î3 = 16
Soluția c
RÎ = Î3 - Î1 = 16 - 9 = 7 puncte.
Care, așa cum vedem, este mult mai mic decât intervalul de date calculat în secțiunea a), deoarece scorul minim a fost de 1 punct, o valoare mult mai departe de restul..
Referințe
- Berenson, M. 1985. Statistici pentru management și economie. Interamericana S.A.
- Canavos, G. 1988. Probabilitate și statistici: aplicații și metode. Dealul Mcgraw.
- Devore, J. 2012. Probabilități și statistici pentru inginerie și știință. A 8-a. Ediție. Cengage.
- Exemple de quartile. Recuperat de la: matematicas10.net.
- Levin, R. 1988. Statistici pentru administratori. Al 2-lea. Ediție. Prentice hall.
- Walpole, R. 2007. Probabilități și statistici pentru inginerie și științe. Pearson.


Nimeni nu a comentat acest articol încă.