Ce este viteza liniară? (Cu exerciții rezolvate)

viteza liniară este definit ca ceea ce este întotdeauna tangențial la calea urmată de particulă, indiferent de forma ei. Dacă particula se mișcă întotdeauna pe o cale rectilinie, nu există nicio problemă în a ne imagina cum vectorul viteză urmează această linie dreaptă.

Cu toate acestea, în general, mișcarea se efectuează pe o curbă în formă arbitrară. Fiecare porțiune a curbei poate fi modelată ca și cum ar fi parte a unui cerc de rază la, care în fiecare punct este tangentă la calea urmată.

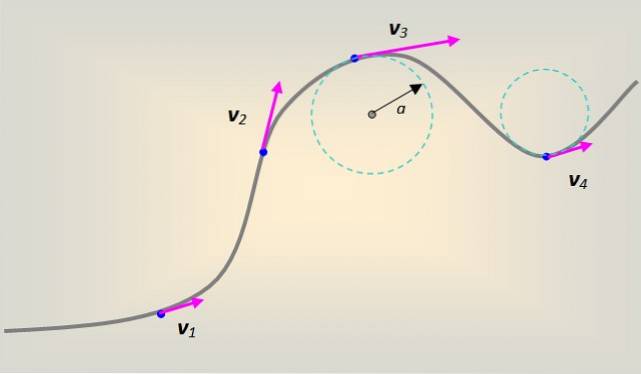
În acest caz, viteza liniară însoțește curba tangențial și în orice moment în fiecare punct al acesteia..

Din punct de vedere matematic, viteza liniară instantanee este derivata poziției față de timp. Fi r vectorul de poziție al particulei într-o clipă t, atunci viteza liniară este dată de expresia:

v = r„(t) = dr / dt

Aceasta înseamnă că viteza liniară sau viteza tangențială, așa cum se numește deseori, nu este altceva decât schimbarea de poziție în raport cu timpul..

Indice articol

• 1 Viteza liniară în mișcare circulară
  • 1.1 Viteza liniară, viteza unghiulară și accelerația centripetă
  • 1.2 - Exercițiu rezolvat 1 
  • 1.3 - Exercițiu rezolvat 2
• 2 Referințe

Viteza liniară în mișcare circulară

Când mișcarea este pe o circumferință, putem merge lângă particulă în fiecare punct și putem vedea ce se întâmplă în două direcții foarte speciale: una dintre ele este cea care indică întotdeauna spre centru. Aceasta este adresa radial.

Cealaltă direcție importantă este cea care trece pe circumferință, aceasta este direcția tangenţial iar viteza liniară o are întotdeauna.

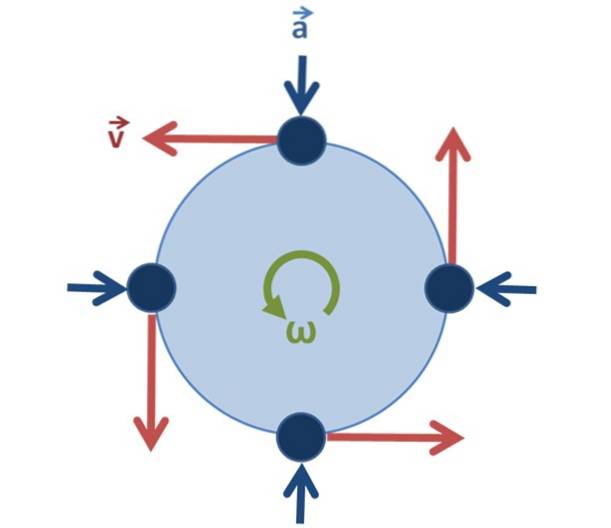
În cazul mișcării circulare uniforme, este important să ne dăm seama că viteza nu este constantă, deoarece vectorul își schimbă direcția pe măsură ce particula se rotește, dar modulul său (dimensiunea vectorului), care este viteza, da rămâne neschimbat.

Pentru această mișcare poziția în funcție de timp este dată de s (t), Unde s este el arc run Da t Este timpul. În acest caz, viteza instantanee este dată de expresie v = ds / dt și este constant.

Dacă magnitudinea vitezei variază și (știm deja că direcția merge întotdeauna, altfel mobilul nu ar putea roti), ne confruntăm cu o mișcare circulară variată, în timpul căreia, pe lângă rotire, poate frâna sau accelera..

Viteza liniară, viteza unghiulară și accelerația centripetă

Mișcarea particulei poate fi văzută și din punctul de vedere al unghi măturat, în loc să o facă din arcadă. Într-un astfel de caz vorbim de viteză unghiulară. Pentru o mișcare pe o circumferință de rază R, există o relație între arc (în radiani) și unghi:

s = R θ

Derivați în ceea ce privește timpul de ambele părți:

ds / dt = R (dθ/ dt)

Apelarea derivatului lui θ cu privire la t Ce viteză unghiulară și denotând-o cu litera greacă ω „omega”, avem această relație:

v = ωR

Accelerație centripetă

Toată mișcarea circulară are accelerație centripetă, care este întotdeauna îndreptată spre centrul circumferinței. Ea se asigură că viteza se schimbă pentru a se deplasa cu particula pe măsură ce se rotește.

Accelerație centripetă la_c sau la_R arată întotdeauna spre centru (vezi figura 2) și este legat de viteza liniară astfel:

la_c = v^Două / R

Și cu viteza unghiulară ca:

la_c = (ωR)^Două / R = ω^DouăR

Pentru o mișcare circulară uniformă, poziția s (t) este de forma:

s (t) = so + vt

Mai mult, mișcarea circulară variată trebuie să aibă o componentă a accelerației numită accelerare tangențială la_T, care se ocupă cu schimbarea magnitudinii vitezei liniare. da la_T  este constant, poziția este:

s (t) = s_sau + v_saut + ½ a_Tt^Două

Cu v_sau ca viteză inițială.

S-au rezolvat probleme de viteză liniară

Exercițiile rezolvate ajută la clarificarea utilizării corecte a conceptelor și ecuațiilor date mai sus..

-Exercițiu rezolvat 1 

O insectă se mișcă pe un semicerc de rază R = 2 m, începând de la repaus în punctul A în timp ce își mărește viteza liniară, cu o rată de p m / s^Două. Găsiți: a) După cât timp atinge punctul B, b) Vectorul vitezei liniare în acel moment, c) Vectorul de accelerație în acel moment.

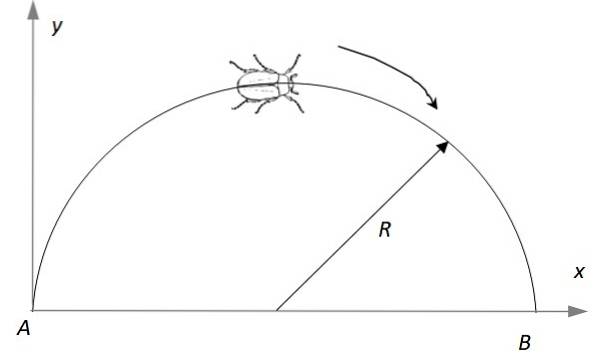
Soluţie

a) Afirmația indică faptul că accelerația tangențială este constantă și este egală cu π m / s^Două, atunci este valabil să folosiți ecuația pentru mișcări uniform variate:

s (t) = s_sau + v_saut + ½ a_T.t^Două

Cu s_sau = 0 și v_sau = 0:

s (t) = ½ a_T.t^Două

s = πR (Jumătate din lungimea circumferinței)

t = (2. πR /la_T) ^½ s = (2π.2 / π)^½s = 2 s

b) v (t) = v_sau + la_T. t = 2π Domnișoară

Când se află în punctul B, vectorul vitezei liniare indică în direcția verticală în jos în direcția (-Da):

v (t) = 2π Domnișoară(-Da)

c) Avem deja accelerația tangențială, accelerarea centripetă lipsește pentru a avea vectorul viteză la:

la_c = v^Două / R = (2π)^Două / 2 m / s^Două = 2π^Două Domnișoară^Două

la = a_c (-X) + a_T (-Da) = 2π^Două(-X) + π (-Da) Domnișoară^Două

-Exercițiu rezolvat 2

O particulă se rotește într-un cerc de rază 2,90 m. La un moment dat, accelerația sa este de 1,05 m / s^Două într-o direcție astfel încât să se formeze 32 ° cu direcția sa de mișcare. Găsiți-i viteza liniară la: a) Acest moment, b) 2 secunde mai târziu, presupunând că accelerația tangențială este constantă.

Soluţie

a) Direcția mișcării este tocmai direcția tangențială:

la_T = 1,05 m / s^Două . cos 32º = 0,89 m / s^Două ; la_C = 1,05 m / s^Două . sin 32º = 0,56 m / s^Două

Viteza se elimină de la la_c = v^Două / R Ce:

v = (R.a_c)^1/2  = 1,27 m / s

b) Următoarea ecuație este valabilă pentru mișcări uniform variate: v = v_sau + la_Tt = 1,27 + 0,89 .2^Două m / s = 4,83 m / s

Referințe

1. Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Seria de fizică pentru științe și inginerie. Volumul 3. Ediție. Cinematică. 199-232.
3. Giancoli, D. 2006. Fizică: principii cu aplicații. 6^a… Ed Prentice Hall. 62-64.
4. Mișcare relativă. Recuperat de la: courses.lumenlearning.com
5. Wilson, J. 2011. Fizică 10. Pearson Education. 166-168.