Reducerea termenilor similari (cu exerciții rezolvate)

reducerea termenilor similari este o metodă utilizată pentru simplificarea expresiilor algebrice. Într-o expresie algebrică, termeni asemănători sunt cei care au aceeași variabilă; adică au aceleași necunoscute reprezentate de o literă, iar aceștia au aceiași exponenți.

În unele cazuri, polinoamele sunt extinse și pentru a ajunge la o soluție trebuie să încercați să reduceți expresia; Acest lucru este posibil atunci când există termeni similari, care pot fi combinați prin aplicarea operațiilor și a proprietăților algebrice, cum ar fi adunarea, scăderea, multiplicarea și divizarea..

Indice articol

• 1 Explicație
• 2 Cum se face o reducere a termenilor similari?
  • 2.1 Exemplu
  • 2.2 Reducerea termenilor similari cu semne egale
  • 2.3 Reducerea termenilor similari cu semne diferite
• 3 Reducerea termenilor similari în operațiuni
  • 3.1 În sume
  • 3.2 În scădere
  • 3.3 În multiplicare
  • 3.4 În diviziuni
• 4 exerciții rezolvate
  • 4.1 Primul exercițiu
  • 4.2 Al doilea exercițiu
• 5 Referințe

Explicaţie

Termeni similari sunt formați din aceleași variabile cu aceiași exponenți și, în unele cazuri, aceștia sunt diferențiați doar prin coeficienții lor numerici.

Termenii asemănători sunt de asemenea considerați cei care nu au variabile; adică acei termeni care au numai constante. Deci, de exemplu, următorii sunt termeni ca:

- 6x^Două - 3x^Două. Ambii termeni au aceeași variabilă x^Două.

- Al 4-lea^Douăb³ + Al 2-lea^Douăb³. Ambii termeni au aceleași variabile a^Douăb³.

- 7 - 6. Termenii sunt constanți.

Acei termeni care au aceleași variabile, dar cu exponenți diferiți, sunt numiți termeni diferiți, cum ar fi:

- 9a^Douăb + 5ab. Variabilele au exponenți diferiți.

- 5x + și. Variabilele sunt diferite.

- b - 8. Un termen are o variabilă, celălalt este o constantă.

Identificând termenii similari care formează un polinom, aceștia pot fi reduși la unul, combinând toți aceia care au aceleași variabile cu aceiași exponenți. În acest fel, expresia este simplificată prin reducerea numărului de termeni care o compun și se facilitează calculul soluției sale..

Cum se face o reducere a termenilor similari?

Reducerea termenilor similari se face prin aplicarea proprietății asociative a adunării și a proprietății distributive a produsului. Utilizând următoarea procedură puteți face o reducere la termen:

- Ca și termenii sunt grupați mai întâi.

- Coeficienții (numerele care însoțesc variabilele) termenilor similari se adaugă sau se scad, iar proprietățile asociative, comutative sau distributive sunt aplicate, după caz..

- Apoi se scriu noii termeni obținuți, plasându-se în fața lor semnul care a rezultat din operațiune.

Exemplu

Reduceți termenii următoarei expresii: 10x + 3y + 4x + 5y.

Soluţie

În primul rând, termenii sunt ordonați să grupeze pe cei care sunt similari, aplicând proprietatea comutativă:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Apoi se aplică proprietatea distributivă și se adaugă coeficienții care însoțesc variabilele pentru a obține reducerea termenilor:

10x + 4x + 3y + 5y

= (10 + 4) x + (3 + 5) y

= 14x + 8y.

Pentru a reduce termeni similari, este important să se ia în considerare semnele coeficienților care însoțesc variabila. Există trei cazuri posibile:

Reducerea termenilor similari cu semne egale

În acest caz, se adaugă coeficienții și semnul termenilor este plasat în fața rezultatului. Prin urmare, dacă sunt pozitivi, termenii rezultați vor fi pozitivi; în cazul în care termenii sunt negativi, rezultatul va avea semnul (-) însoțit de variabilă. De exemplu:

a) 22ab^Două + 12ab^Două = 34 ab^Două.

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Reducerea termenilor similari cpe diferite semne

În acest caz, se scad coeficienții, iar semnul celui mai mare coeficient este plasat în fața rezultatului. De exemplu:

a) 15x^Douăy - 4x^Douăși + 6x^Douăy - 11x^DouăDa

= (15x^Douăși + 6x^Douăy) + (- 4x^Douăy - 11x^DouăY)

= 21x^Douăy + (-15x^DouăY)

= 21x^Douăy - 15x^DouăDa

= 6x^DouăDa.

b) -5a³b + 3 a³b - 4a³b + a³b

= (3 până la³b + a³b) + (-5a³b - 4a³b)

= 4a³b - 9a³b

= -5 până la³b.

Astfel, pentru a reduce termeni similari care au semne diferite, se formează un singur termen aditiv cu toți cei care au semn pozitiv (+), se adaugă coeficienții și rezultatul este însoțit de variabile.

În același mod, se formează un termen subtractiv, cu toți acei termeni care au semn negativ (-), se adaugă coeficienții și rezultatul este însoțit de variabile.

În cele din urmă, sumele celor doi termeni formați se scad, iar semnul celui mai mare este plasat din rezultat.

Reducerea termenilor similari în operațiuni

Reducerea termenilor similari este o operație de algebră, care poate fi aplicată în plus, scădere, înmulțire și diviziune algebrică.

În sume

Când aveți mai mulți polinoame cu termeni similari, pentru a le reduce, termenii fiecărui polinom sunt ordonați păstrându-și semnele, apoi se scriu unul după altul și termenii similari sunt reduși. De exemplu, avem următoarele polinoame:

3x - 4xy + 7x^Douăși + 5xy^Două.

- 6x^Douăy - 2xy + 9 xy^Două - 8x.

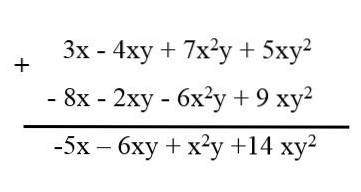
În scădere

Pentru a scădea un polinom din altul, se scrie minuendul și apoi subtrahendul cu semnele sale s-a schimbat, apoi se face reducerea termenilor similari. De exemplu:

Al 5-lea³ - 3ab^Două + 3b^Douăc

6ab^Două + Al 2-lea³ - 8b^Douăc

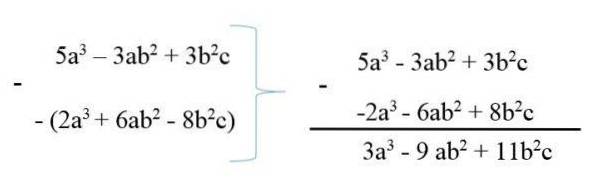
Astfel, polinoamele sunt rezumate la 3a³ - 9ab^Două + 11b^Douăc.

În multiplicări

Într-un produs de polinoame, termenii care alcătuiesc multiplicatorul sunt înmulțiți cu fiecare termen care alcătuiește multiplicatorul, considerând că semnele înmulțirii rămân aceleași dacă sunt pozitive.

Ele vor fi schimbate numai atunci când sunt înmulțite cu un termen care este negativ; adică, atunci când doi termeni ai aceluiași semn sunt înmulțiți, rezultatul va fi pozitiv (+), iar atunci când au semne diferite, rezultatul va fi negativ (-).

De exemplu:

a) (a + b) _* (a + b)

= a^Două + ab + ab + b^Două

= a^Două + 2ab + b^Două.

b) (a + b) _* (a - b)

= a^Două - ab + ab - b^Două

= a^Două - b^Două.

taxi) _* (a - b)

= a^Două - ab - ab + b^Două

= a^Două - 2ab + b^Două.

În diviziuni

Când doriți să reduceți două polinoame printr-o diviziune, trebuie să găsiți un al treilea polinom care, atunci când este înmulțit cu al doilea (divizor), are ca rezultat primul polinom (dividend).

Pentru aceasta, termenii dividendului și divizorului trebuie ordonați, de la stânga la dreapta, astfel încât variabilele din ambele să fie în aceeași ordine.

Apoi se efectuează împărțirea, începând de la primul termen din stânga dividendului cu primul termen din stânga divizorului, ținând cont întotdeauna de semnele fiecărui termen.

De exemplu, reduceți polinomul: 10x⁴ - 48x³și + 51x^DouăDa^Două + 4xy³ - 15 ani⁴ împărțindu-l la polinomul: -5x^Două + 4xy + 3y^Două.

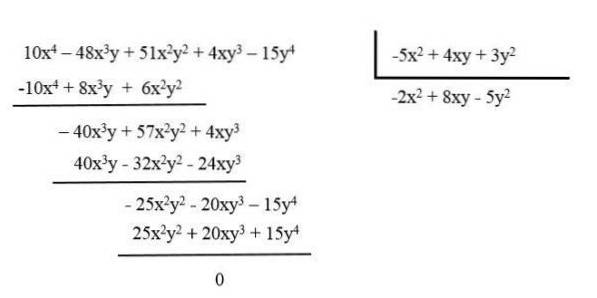
Polinomul rezultat este -2x^Două + 8xy - 5y^Două.

Exerciții rezolvate

Primul exercițiu

Reduceți termenii expresiei algebrice date:

15^Două - 8ab + 6a^Două - 6ab - 9 + 4a^Două - 13 ab.

Soluţie

Se aplică proprietatea comutativă a adunării, grupând termenii care au aceleași variabile:

15^Două - 8ab + 6a^Două - 6ab + 9 + 4a^Două - 13

= (15a^Două + Al 6-lea^Două + Al 4-lea^Două) + (- 8ab - 6ab) + (9-13).

Atunci se aplică proprietatea distributivă a multiplicării:

15^Două - 8ab + 6a^Două - 6ab + 9 + 4a^Două - 13

= (15 + 6 + 4) a^Două + (- 8 - 6) ab + (9 - 13).

În cele din urmă, acestea sunt simplificate prin adăugarea și scăderea coeficienților fiecărui termen:

15^Două - 8ab + 6a^Două - 6ab + 9 + 4a^Două - 13

= 25a^Două - 14ab - 4.

Al doilea exercițiu

Simplificați produsul următoarelor polinoame:

(8x³ + 7xy^Două)_*(8x³ - 7 xy^Două).

Soluţie

Fiecare termen al primului polinom este înmulțit cu al doilea, ținând cont că semnele termenilor sunt diferite; prin urmare, rezultatul înmulțirii sale va fi negativ, precum și legile exponenților trebuie aplicate.

(8x³ + 7xy^Două) _* (8x³ - 7xy^Două)

= 64 x⁶ - 56 x³_* X y^Două + 56 x³_* X y^Două - 49 x^DouăDa⁴

= 64 x⁶ - 49 x^DouăDa⁴.

Referințe

1. Angel, A. R. (2007). Algebra elementară. Pearson Education,.
2. Baldor, A. (1941). Algebră. Havana: Cultură.
3. Jerome E. Kaufmann, K. L. (2011). Algebră elementară și intermediară: o abordare combinată. Florida: Cengage Learning.
4. Smith, S. A. (2000). Algebră. Pearson Education.
5. Vigil, C. (2015). Algebra și aplicațiile sale.