
Semicerc cum să calculați perimetrul, aria, centroidul, exercițiile
semicerc este o figură plană delimitată de un diametru al circumferinței și unul dintre cele două arce circulare plate determinate de respectivul diametru.
În acest fel, un semicerc este mărginit de un semicircumferinta, care constă dintr-un arc circular circular și un segment drept care unește capetele arcului circular circular. Semicercul cuprinde semicercul și toate punctele din interiorul acestuia..
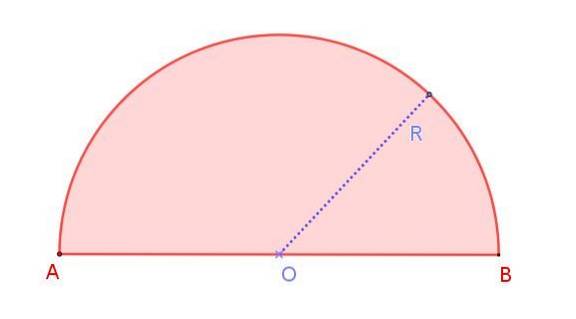
Putem vedea acest lucru în figura 1, care arată un semicerc de rază R, a cărui măsură este jumătate din diametrul AB. Rețineți că, spre deosebire de un cerc, în care există diametre infinite, în semicircumferință există un singur diametru.
Semicercul este o figură geometrică cu multe utilizări în arhitectură și design, așa cum vedem în următoarea imagine:

Indice articol
- 1 Elemente și măsuri ale unui semicerc
- 1.1 Perimetrul unui semicerc
- 1.2 Aria unui semicerc
- 1.3 Centroidul unui semicerc
- 1.4 Momentul de inerție al unui semicerc
- 1.5 Unghiul înscris
- 2 exerciții rezolvate
- 2.1 Exercițiul 1
- 2.2 Exercițiul 2
- 2.3 Exercițiul 3
- 2.4 Exercițiul 4
- 2.5 Exercițiul 5
- 3 Referințe
Elemente și măsuri ale unui semicerc
Elementele unui semicerc sunt:
1.- Arcul circular circular A⌒B
2.- Segmentul [AB]
3.- Punctele din interiorul semicercului compus din arcul A⌒B și segmentul [AB].
Perimetrul unui semicerc
Perimetrul este suma conturului arcului plus cel al segmentului drept, prin urmare:
Perimetru = lungimea arcului A⌒B + lungimea segmentului [AB]
În cazul unui semicerc de rază R, perimetrul său P va fi dat de formula:
P = π⋅R + 2⋅R = (π + 2) ⋅R
Primul termen este jumătate din perimetrul unui cerc de rază R, în timp ce al doilea este lungimea diametrului, care este de două ori mai mare decât raza..
Zona unui semicerc
Deoarece un semicerc este unul dintre sectoarele unghiulare plane care rămân la trasarea unui diametru prin circumferință, aria sa va fi jumătate din aria cercului care conține semicercul de rază R:
A = (π⋅RDouă) / 2 = ½ π⋅RDouă
Centroid al unui semicerc
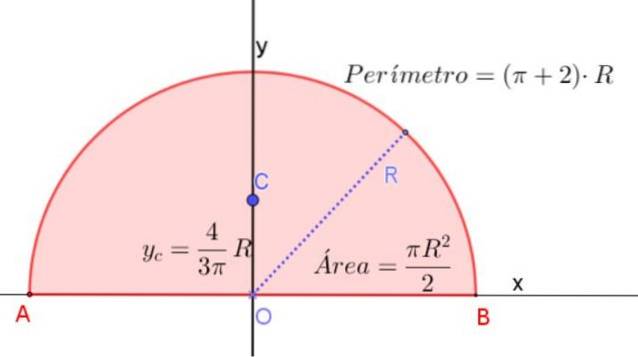
Centroidul unui semicerc este pe axa sa de simetrie la o înălțime măsurată de la diametrul său de 4 / (3π) ori mai mare decât raza R.
Aceasta corespunde la aproximativ 0,424⋅R, măsurată din centrul semicercului și pe axa sa de simetrie, așa cum se arată în figura 3.
Momentul de inerție al unui semicerc
Momentul de inerție al unei figuri plane față de o axă, de exemplu axa x, este definit ca:
Integrala pătratului distanței punctelor aparținând figurii la axă, diferențialul de integrare fiind un element de zonă infinitesimal, luat la poziția fiecărui punct.
Figura 4 prezintă definiția momentului de inerție IX semicercului de rază R, în raport cu axa X care trece prin diagonala sa:
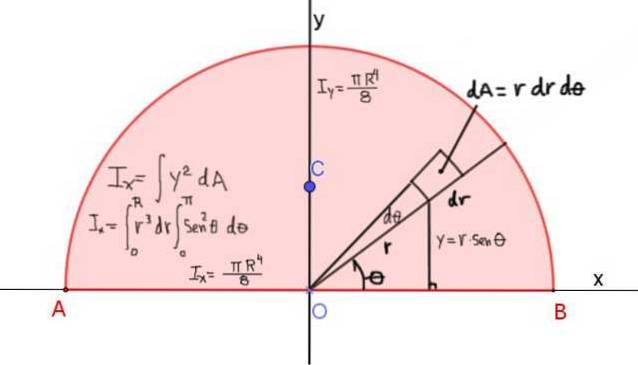
Momentul de inerție despre axa x este dat de:
EuX = (π⋅R4) / 8
Iar momentul de inerție față de axa de simetrie y este:
Iy = (π⋅R4) / 8
Se observă că ambele momente de inerție coincid în formula lor, dar este important de reținut că se referă la diferite axe.
Unghiul înscris
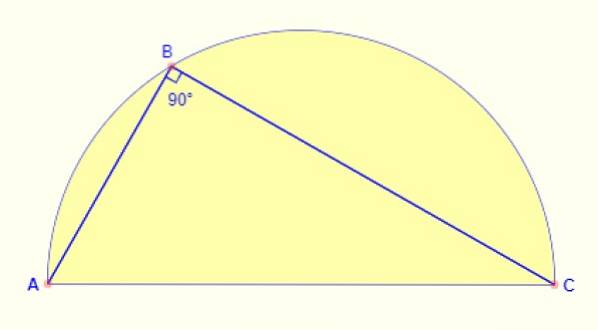
Unghiul înscris în semicerc este întotdeauna de 90º. Indiferent de locul în care este luat punctul pe arc, unghiul format între laturile AB și BC ale figurii este întotdeauna corect..
Exerciții rezolvate
Exercitiul 1
Determinați perimetrul unui semicerc cu raza de 10 cm.
Soluţie
Amintiți-vă că perimetrul în funcție de rază este dat de formula pe care am văzut-o mai devreme:
P = (2 + π) ⋅R
P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.
Exercițiul 2
Găsiți aria unui semicerc cu raza de 10 cm.
Soluţie
Formula pentru aria unui semicerc este:
A = ½ π⋅RDouă = ½ π⋅ (10cm)Două = 50π cmDouă = 50 x 3,14 cmDouă = 157 cmDouă.
Exercițiul 3
Determinați înălțimea h a centrului unui semicerc cu raza R = 10 cm măsurată de la baza acestuia, diametrul semicercului fiind același.
Soluţie
Centroidul este punctul de echilibru al semicercului și poziția sa este pe axa de simetrie la o înălțime h de la bază (diametrul semicercului):
h = (4⋅R) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4,246 cm
Exercițiul 4
Găsiți momentul de inerție al unui semicerc în raport cu axa care coincide cu diametrul acestuia, știind că semicercul este format dintr-o foaie subțire. Raza sa este de 10 cm și masa sa este de 100 de grame.
Soluţie
Formula care dă momentul de inerție al semicercului este:
EuX = (π⋅R4) / 8
Dar deoarece problema ne spune că este un semicerc material, atunci relația anterioară trebuie să fie înmulțită cu densitatea suprafeței de masă a semicercului, care va fi notată cu σ.
EuX = σ (π⋅R4) / 8
Apoi procedăm la determinarea σ, care nu este altceva decât masa semicercului împărțită la aria sa.
Zona a fost determinată în exercițiul 2 și rezultatul a fost de 157 cmDouă. Atunci densitatea suprafeței acestui semicerc va fi:
σ = 100 grame / 157 cmDouă = 0,637 g / cmDouă
Atunci momentul de inerție în raport cu diametrul va fi calculat astfel:
EuX = (0,637 g / cmDouă) [3,1416 ⋅ (10cm)4] / 8
Rezultând:
EuX = 2502 g⋅cmDouă
Exercițiul 5
Determinați momentul de inerție al unui semicerc cu raza de 10 cm dintr-o foaie de material cu densitatea suprafeței de 0,637 g / cmDouă de-a lungul unei axe care trece prin centroidul său și este paralel cu diametrul său.
Soluţie
Pentru a rezolva acest exercițiu, este necesar să ne amintim de teorema lui Steiner asupra momentelor de inerție a axelor paralele, care spune:
Momentul de inerție I față de o axă care se află la o distanță h de centroid este egal cu suma momentului de inerție Ic în ceea ce privește o axă care trece prin centroid și este paralelă cu primul plus produsul masei ori pătratul separării celor două axe.
Eu = euc + M hDouă
În cazul nostru, se știe I care este momentul de inerție în raport cu diametrul, care a fost deja calculat în exercițiul 4. Se cunoaște, de asemenea, separarea h între diametru și centroid, care a fost calculată în exercițiul 3.
Trebuie doar să ștergem Ic:
Euc = I - M hDouă
Euc = 2502 g⋅cmDouă - 100g 4. (4.246 cm)Două rezultând că momentul de inerție printr-o axă paralelă cu diametrul și care trece prin centroid este:
Euc = 699,15 g⋅cmDouă
Referințe
- Alexander, D. 2013. Geometrie. Al 5-lea. Ediție. Cengage Learning.
- Math Open Reference. Semicerc. Recuperat de pe: mathopenref.com.
- Formulele Universului Semicerc. Recuperat de pe: universoformulas.com.
- Formulele Universului. Zona unui semicerc. Recuperat de pe: universoformulas.com.
- Wikipedia. Semicerc. Recuperat de pe: en.wikipedia.com.


Nimeni nu a comentat acest articol încă.