Exemple de secvențe cuadratice, reguli și exerciții rezolvate

secvențe pătratice, în termeni matematici, acestea constau din secvențe de numere care urmează o anumită regulă aritmetică. Este interesant să cunoașteți această regulă pentru a determina oricare dintre termenii unei secvențe.

O modalitate de a realiza acest lucru este de a determina diferența dintre doi termeni succesivi și de a vedea dacă valoarea obținută este întotdeauna repetată. Când acesta este cazul, se spune că este un succesiunea regulată.

Dar dacă nu se repetă, atunci puteți încerca să examinați diferența dintre diferențe și vezi dacă această valoare este constantă. Dacă da, atunci este un secvență pătratică. 

Indice articol

• 1 Exemple de secvențe regulate și secvențe pătratice
  • 1.1 Exemplu de succesiune regulată
  • 1.2 Exemplu de secvență neregulată și pătratică
• 2 Regula generală pentru construirea unei secvențe pătratice
  • 2.1 Diferența dintre doi termeni consecutivi ai unei secvențe pătratice
• 3 Probleme rezolvate ale secvențelor pătratice
  • 3.1 Exercițiul 1
  • 3.2 Exercițiul 2
  • 3.3 Exercițiul 3
• 4 Referințe

Exemple de secvențe regulate și secvențe pătratice

Următoarele exemple ajută la clarificarea celor explicate până acum:

Exemplu de succesiune regulată

Fie secvența S = 4, 7, 10, 13, 16, ...

Această succesiune, notată cu S, este o mulțime numerică infinită, în acest caz a numerelor întregi.

Se poate vedea că este o secvență regulată, deoarece fiecare termen este obținut prin adăugarea a 3 la termenul sau elementul anterior:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Cu alte cuvinte: această secvență este regulată, deoarece diferența dintre termenul următor și cel anterior oferă o valoare fixă. În exemplul dat această valoare este 3.

Se mai numesc și secvențele regulate care se obțin prin adăugarea unei cantități fixe la termenul anterior progresii aritmetice. Iar diferența -constantă- între termenii succesivi se numește motiv și este notat ca R.

Exemplu de secvență neregulată și pătratică

Vedeți acum următoarea secvență:

S = 2, 6, 12, 20, 30,….

Când sunt calculate diferențele succesive, se obțin următoarele valori:

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Diferențele sale nu sunt constante, deci se poate spune că este o secvență NU regulată.

Totuși, dacă luăm în considerare setul de diferențe, avem o altă secvență, care va fi notată ca S_dif:

S_dif = 4, 6, 8, 10,….

Această nouă succesiune este o succesiunea regulată, întrucât fiecare termen se obține prin adăugarea valorii fixe R = 2 la cea anterioară. Prin urmare, putem afirma că S este secvență pătratică.

Regula generală pentru construirea unei secvențe pătratice

Există o formulă generală pentru a construi o succesiune pătratică:

T_n = A ∙ n^Două + B ∙ n + C

În această formulă, T_n este termenul de poziție n al secvenței. A, B și C sunt valori fixe, în timp ce n variază unul câte unul, adică 1, 2, 3, 4, ...

În secvența S a exemplului anterior A = 1, B = 1 și C = 0. De acolo rezultă că formula care generează toți termenii este: T_n = n^Două + n

Și anume:

T₁ = 1^Două + 1 = 2

T_Două = 2^Două + 2 = 6

T₃ = 3^Două + 3 = 12

T₅ = 5^Două + 5 = 30

T_n = n^Două + n

Diferența dintre doi termeni consecutivi ai unei secvențe pătratice

T_{n + 1} - T_n = [A ∙ (n + 1)^Două + B ∙ (n + 1) + C] - [A ∙ n^Două + B ∙ n + C]

Dezvoltarea expresiei prin produs remarcabil rămâne:

T_{n + 1} - T_n = A ∙ n^Două + A ∙ 2 ∙ n + A + B ∙ n + B + C - A ∙ n^Două - B ∙ n - C

Prin simplificarea acestuia, veți obține:

T_{n + 1} - T_n = 2 ∙ A ∙ n + A + B

Aceasta este formula care dă secvența diferențelor S_Dif care poate fi scris astfel:

Dif_n = A ∙ (2n + 1) + B

Unde clar termenul următor este 2 ∙ Uneori cel anterior. Adică raportul secvenței diferențelor S_dif este: R = 2 ∙ A.

S-au rezolvat probleme ale secvențelor pătratice

Exercitiul 1

Fie secvența S = 1, 3, 7, 13, 21, .... Determinați dacă:

i) Este regulat sau nu

ii) Este pătratic sau nu

iii) Era pătratică, secvența diferențelor și raportul lor

Răspunsuri

i) Să calculăm diferența dintre următorii termeni și anteriori:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

Putem afirma asta secvența S nu este regulată, deoarece diferența dintre termenii succesivi nu este constantă.

ii) Succesiunea diferențelor este regulată, deoarece diferența dintre termenii săi este valoarea constantă 2. Prin urmare secvența originală S este pătratică.

iii) Am stabilit deja că S este pătratic, succesiunea diferențelor este:

S_dif = 2, 4, 6, 8, ... și raportul său este R = 2.

Exercițiul 2

Fie secvența S = 1, 3, 7, 13, 21, ... din exemplul anterior, unde s-a verificat că este pătratică. A determina:

i) Formula care determină termenul general T_{n .}

ii) Verificați al treilea și al cincilea termen.

iii) Valoarea celui de-al zecelea termen.

Răspunsuri

i) Formula generală a lui T_n este A ∙ n^Două + B ∙ n + C. Apoi rămâne să cunoaștem valorile lui A, B și C.

Secvența diferențelor are raportul 2. Mai mult, pentru orice secvență pătratică raportul R este de 2 ∙ A așa cum se arată în secțiunile anterioare.

R = 2 ∙ A = 2 ceea ce ne conduce la concluzia că A = 1.

Primul termen al secvenței diferențelor S_Dif este 2 și trebuie să satisfacă A ∙ (2n + 1) + B, cu n = 1 și A = 1, adică:

2 = 1 ∙ (2 ∙ 1 + 1) + B

rezolvând pentru B, obținem: B = -1

Atunci primul termen al lui S (n = 1) valorează 1, adică: 1 = A ∙ 1^Două + B ∙ 1 + C. După cum știm deja că A = 1 și B = -1, înlocuind avem:

1 = 1 ∙ 1^Două + (-1) ∙ 1 + C

Rezolvând pentru C obținem valoarea sa: C = 1.

În concluzie:

A = 1, B = -1 și C = 1

Atunci al n-lea termen va fi T_n = n^Două - n + 1

ii) Al treilea termen T₃ = 3^Două - 3 + 1 = 7 și este verificat. Al cincilea T₅ = 5^Două - 5 + 1 = 21 care este, de asemenea, verificat.

iii) Al zecelea termen va fi T₁₀ = 10^Două - 10 + 1 = 91.

Exercițiul 3

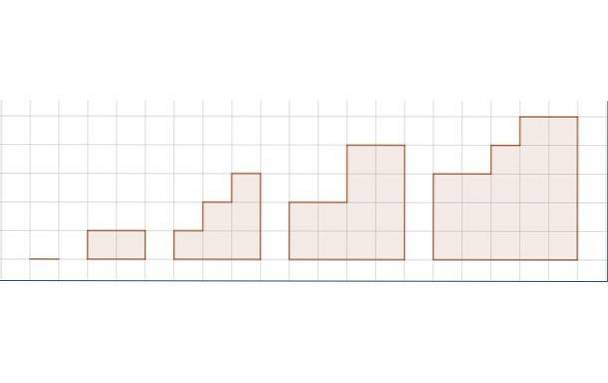
Figura prezintă o succesiune de cinci figuri. Rețeaua reprezintă unitatea de lungime.

i) Determinați secvența pentru aria figurilor.

ii) Arătați că este o secvență pătratică.

iii) Găsiți aria figurii # 10 (nu este prezentată).

Răspunsuri

i) Secvența S corespunzătoare ariei secvenței de figuri este:

S = 0, 2, 6, 12, 20, ...

ii) Secvența corespunzătoare diferențelor consecutive ale termenilor lui S este:

S_dif = 2, 4, 6, 8, ...

Deoarece diferența dintre termenii consecutivi nu este constantă, atunci S nu este o secvență regulată. Rămâne să se știe dacă este pătratic, pentru care facem din nou succesiunea diferențelor, obținând:

2, 2, 2,….

Deoarece toți termenii secvenței sunt repetați, se confirmă că S este o secvență pătratică.

iii) Secvența S_dif este regulat și raportul său R este 2. Folosind ecuația prezentată mai sus R = 2 ∙ A, rămâne:

2 = 2 ∙ A, ceea ce implică faptul că A = 1.

Al doilea termen al secvenței diferențelor S_Dif este 4 și al nouălea termen al lui S_Dif este

A ∙ (2n + 1) + B.

Al doilea termen are n = 2. În plus, sa stabilit deja că A = 1, deci folosind ecuația anterioară și substituind, avem:

4 = 1 ∙ (2 ∙ 2 + 1) + B

Rezolvând pentru B obținem: B = -1.

Se știe că al doilea termen al lui S valorează 2 și că trebuie să îndeplinească formula termenului general cu n = 2:

T_n = A ∙ n^Două + B * n + C; n = 2; A = 1; B = -1; T_Două = 2

Și anume

2 = 1 ∙ 2^Două - 1 ∙ 2 + C

Se concluzionează că C = 0, adică formula care dă termenul general al secvenței S este:

T_n = 1 ∙ n^Două - 1 ∙ n +0 = n^Două - n

Acum al cincilea termen este verificat:

T₅ = 5^Două - 5 = 20

iii) Figura # 10, care nu a fost desenată aici, va avea aria corespunzătoare celui de-al zecelea termen al secvenței S:

T₁₀ = 10^Două - 10 = 90

Referințe

1. https://www.geogebra.org