
Teorema lui Bolzano Explicație, aplicații și exerciții
Teorema lui Bolzano stabilește că dacă o funcție este continuă în toate punctele unui interval închis [a, b] și este adevărat că imaginea „a” și „b” (sub funcție) au semne opuse, atunci va exista cel puțin una punctul "C" în intervalul deschis (a, b), în așa fel încât funcția evaluată în "c" să fie egală cu 0.
Această teoremă a fost enunțată de filosoful, teologul și matematicianul Bernard Bolzano în 1850. Acest om de știință, născut în actuala Republica Cehă, a fost unul dintre primii matematicieni din istorie care au făcut o dovadă formală a proprietăților funcțiilor continue..
Indice articol
- 1 Explicație
- 2 Demo
- 3 Pentru ce este?
- 4 exerciții rezolvate
- 4.1 Exercițiul 1
- 4.2 Exercițiul 2
- 5 Referințe
Explicaţie
Teorema lui Bolzano este cunoscută și sub numele de teorema valorilor intermediare, care ajută la determinarea valorilor specifice, în special a zerourilor, ale anumitor funcții reale ale unei variabile reale.
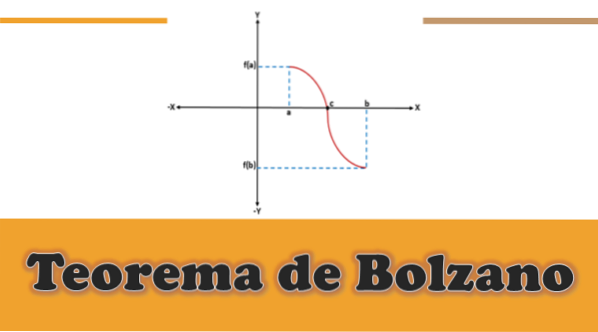
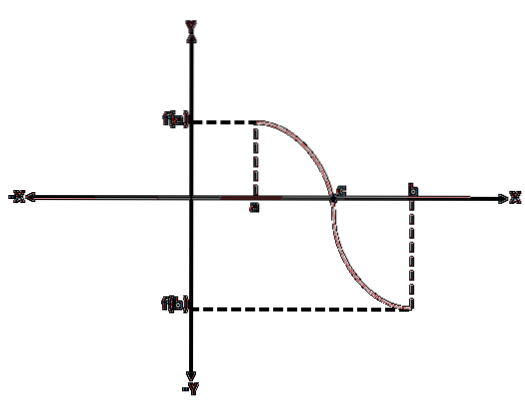
Într-o funcție dată f (x) continuă-adică f (a) și f (b) sunt conectate printr-o curbă-, unde f (a) este sub axa x (este negativă) și f ( b) de deasupra axei x (este pozitiv), sau invers, grafic va exista un punct de tăiere pe axa x care va reprezenta o valoare intermediară „c”, care va fi între „a” și „B”, iar valoarea lui f (c) va fi egală cu 0.
Analizând grafic teorema lui Bolzano, se poate observa că pentru fiecare funcție continuă f definită pe un interval [a, b], unde f (a)*f (b) este mai mic decât 0, va exista cel puțin o rădăcină "c" a acelei funcții în intervalul (a, b).
Această teoremă nu stabilește numărul de puncte în acel interval deschis, ci afirmă doar că există cel puțin 1 punct.
Demonstrație
Pentru a demonstra teorema lui Bolzano, se presupune fără pierderea generalității că f (a) < 0 y f(b) > 0; astfel, pot exista multe valori între „a” și „b” pentru care f (x) = 0, dar este necesar doar să se arate că există una.
Începem prin evaluarea f la punctul mediu (a + b) / 2. Dacă f ((a + b) / 2) = 0 atunci dovada se termină aici; în caz contrar, atunci f ((a + b) / 2) este pozitiv sau negativ.
Se alege una dintre jumătățile intervalului [a, b], astfel încât semnele funcției evaluate la extreme sunt diferite. Acest nou interval va fi [a1, b1].
Acum, dacă f evaluat la mijlocul lui [a1, b1] nu este zero, atunci se efectuează aceeași operație ca înainte; adică se alege o jumătate din acest interval care îndeplinește condiția semnelor. Fie acest nou interval să fie [a2, b2].
Dacă continuați acest proces, atunci veți avea două secvențe an și bn, astfel încât:
an crește și bn scade:
a ≤ a1 ≤ a2 ≤… ≤ an ≤…. ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Dacă se calculează lungimea fiecărui interval [ai, bi], vom avea:
b1-a1 = (b-a) / 2.
b2-a2 = (b-a) / 2².
... .
bn-an = (b-a) / 2 ^ n.
Prin urmare, limita ca n tinde la infinit de (bn-an) este egală cu 0.
Folosind acel an este în creștere și delimitat și bn este în descreștere și delimitat, avem că există o valoare „c” astfel încât:
a ≤ a1 ≤ a2 ≤… ≤ an ≤… .≤ c ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Limita unui este „c”, iar limita lui bn este și „c”. Prin urmare, având în vedere orice δ> 0, există întotdeauna un "n" astfel încât intervalul [an, bn] să fie conținut în interval (c-δ, c + δ).
Acum, trebuie arătat că f (c) = 0.
Dacă f (c)> 0, deoarece f este continuu, există un ε> 0 astfel încât f să fie pozitiv pe întregul interval (c-ε, c + ε). Cu toate acestea, așa cum s-a spus mai sus, există o valoare „n” astfel încât f modifică semnul [an, bn] și, în plus, [an, bn] este conținut în contradicţie.
Dacă f (c) < 0, entonces como f es continua, existe un ε >0 astfel încât f este negativ pe tot parcursul intervalului (c-ε, c + ε); dar există o valoare „n”, astfel încât f modifică semnul [an, bn]. Se pare că [an, bn] este conținut în (c-ε, c + ε), ceea ce este, de asemenea, o contradicție.
Prin urmare, f (c) = 0 și asta am vrut să arătăm.
Pentru ce este?
Din interpretarea sa grafică, teorema lui Bolzano este utilizată pentru a găsi rădăcini sau zerouri într-o funcție continuă, prin bisecție (aproximare), care este o metodă de căutare incrementală care împarte întotdeauna intervalele la 2.
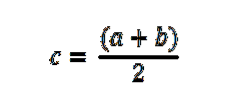
Apoi se ia un interval [a, c] sau [c, b] acolo unde are loc schimbarea semnului și procesul se repetă până când intervalul este din ce în ce mai mic, pentru a se apropia de valoarea dorită; adică la valoarea pe care funcția o face 0.
În rezumat, pentru a aplica teorema lui Bolzano și a găsi astfel rădăcinile, a limita zerourile unei funcții sau a da o soluție la o ecuație, se efectuează următorii pași:
- Se verifică dacă f este o funcție continuă pe intervalul [a, b].
- Dacă intervalul nu este dat, trebuie găsit unul în cazul în care funcția este continuă.
- Se verifică dacă extremele intervalului dau semne opuse atunci când sunt evaluate la f.
- Dacă nu se obțin semne opuse, intervalul trebuie împărțit în două subintervale folosind punctul mediu.
- Evaluați funcția la punctul mediu și verificați dacă ipoteza Bolzano este îndeplinită, unde f (a) * f (b) < 0.
- În funcție de semnul (pozitiv sau negativ) al valorii găsite, procesul se repetă cu un subinterval nou până la îndeplinirea ipotezei menționate mai sus..
Exerciții rezolvate
Exercitiul 1
Determinați dacă funcția f (x) = xDouă - 2, are cel puțin o soluție reală în intervalul [1,2].
Soluţie
Avem funcția f (x) = xDouă - 2. Deoarece este polinom, înseamnă că este continuu pe orice interval.
Se cere să se determine dacă are o soluție reală în intervalul [1, 2], deci acum este necesar doar să se substituie extremele intervalului în funcție pentru a cunoaște semnul acestora și pentru a ști dacă îndeplinesc condiția a fi diferit:
f (x) = xDouă - Două
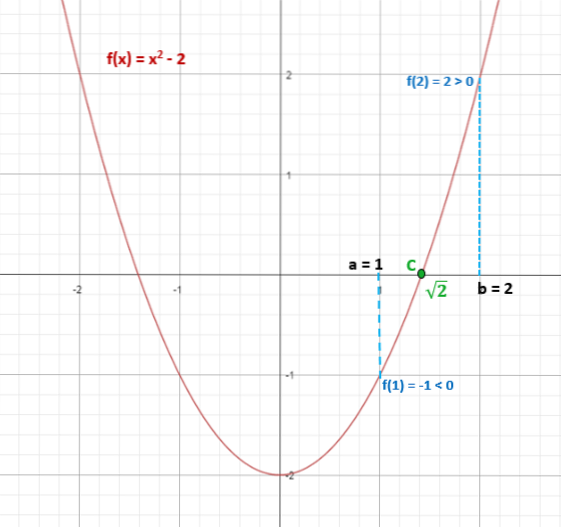
f (1) = 1Două - 2 = -1 (negativ)
f (2) = 2Două - 2 = 2 (pozitiv)
Prin urmare, semnul f (1) ≠ semnul f (2).
Acest lucru asigură că există cel puțin un punct "c" care aparține intervalului [1,2], în care f (c) = 0.
În acest caz, valoarea „c” poate fi ușor calculată după cum urmează:
XDouă - 2 = 0
x = ± √2.
Astfel, √2 ≈ 1,4 aparține intervalului [1,2] și îndeplinește că f (√2) = 0.
Exercițiul 2
Arată că ecuația x5 + x + 1 = 0 are cel puțin o soluție reală.
Soluţie
Să observăm mai întâi că f (x) = x5 + x + 1 este o funcție polinomială, ceea ce înseamnă că este continuă pe toate numerele reale.
În acest caz, nu se acordă niciun interval, deci valorile trebuie alese intuitiv, de preferință apropiate de 0, pentru a evalua funcția și pentru a găsi modificările semnului:
Dacă utilizați intervalul [0, 1] trebuie să:
f (x) = x5 + x + 1.
f (0) = 05 + 0 + 1 = 1> 0.
f (1) = 15 + 1 + 1 = 3> 0.
Deoarece nu există nicio schimbare de semn, procesul se repetă cu un alt interval.
Dacă utilizați intervalul [-1, 0] trebuie să:
f (x) = x5 + x + 1.
f (-1) = (-1)5 + (-1) + 1 = -1 < 0.
f (0) = 05 + 0 + 1 = 1> 0.
În acest interval există o modificare a semnului: semnul lui f (-1) ≠ semnul lui f (0), ceea ce înseamnă că funcția f (x) = x5 + x + 1 are cel puțin o rădăcină reală „c” în intervalul [-1, 0], astfel încât f (c) = 0. Cu alte cuvinte, este adevărat că x5 + x + 1 = 0 are o soluție reală în intervalul [-1,0].
Referințe
- Bronshtein I, S. K. (1988). Manual de matematică pentru ingineri și studenți ... Editorial MIR.
- George, A. (1994). Matematică și minte. presa Universitatii Oxford.
- Ilín V, P. E. (1991). Analiza matematică. În trei volume ...
- Jesús Gómez, F. G. (2003). Profesori de învățământ secundar. Volumul II. NEBUN.
- Mateos, M. L. (2013). Proprietățile de bază ale analizei în R. Editores, 20 dec.
- Piskunov, N. (1980). Calcul diferențial și integral ...
- Sydsaeter K, H. P. (2005). Matematică pentru analiza economică. Felix Varela.
- William H. Barker, R. H. (s.f.). Simetrie continuă: de la Euclid la Klein. American Mathematical Soc.

Nimeni nu a comentat acest articol încă.