
Caracteristici ale planului orizontal, formule și ecuații, exerciții
împușcare orizontală Este lansarea unui proiectil cu viteză orizontală de la o anumită înălțime și lăsat la acțiunea gravitației. Fără a lua în considerare rezistența aerului, traseul descris de mobil va avea forma unui arc de parabolă.
Proiectarea obiectelor pe orizontală este destul de obișnuită. Proiectilele sunt lansate pentru tot felul de scopuri: de la pietrele cu care au fost lovite barajele la începutul poveștii, până la cele desfășurate în sporturile cu minge și sunt urmate îndeaproape de mulțimi.
Indice articol
- 1 Caracteristici
- 2 Formule și ecuații
- 2.1 Poziția, viteza, timpul de zbor și intervalul orizontal maxim
- 3 exerciții rezolvate
- 3.1 -Exercițiu rezolvat 1
- 3.2 - Exercițiu rezolvat 2
- 4 Referințe
Caracteristici
Principalele caracteristici ale fotografiei orizontale sunt:
-Viteza inițială dată proiectilului este perpendiculară pe gravitație.
-Mișcarea are loc într-un plan, deci are două coordonate: X Da Da.
-Se face de la o anumită înălțime H deasupra nivelului solului.
-Timpul durează proiectilul în aer timp de zbor.
-Factori precum rezistența aerului și fluctuațiile valorii g.
-Forma, dimensiunea și masa proiectilului nu influențează mișcarea acestuia.
-Mișcarea este descompusă în două mișcări simultane: una verticală în jos sub acțiunea g; cealaltă, orizontală, cu viteză constantă.
Formule și ecuații
Ecuațiile cinematice pentru lansarea orizontală sunt obținute din ecuațiile pentru cădere liberă și cele pentru mișcare rectilinie uniformă..
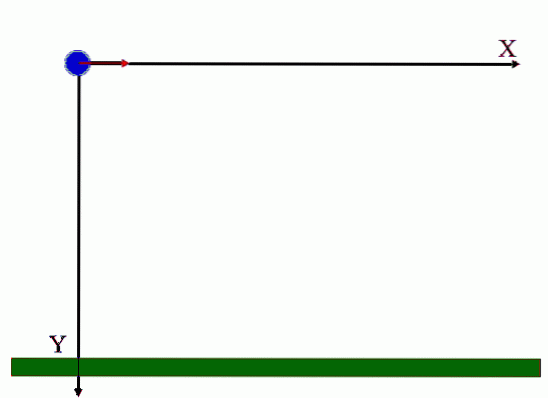
După cum arată animația din Figura 1, proiectilului i se dă o viteză inițială orizontală, notată ca vsau = vbou eu (cu caractere aldine în textul tipărit indică faptul că este un vector).
Rețineți că viteza inițială are magnitudine vbou și este îndreptat de-a lungul axei X, care este direcția vectorului unitar eu. Animația arată, de asemenea, că viteza inițială nu are o componentă verticală, dar pe măsură ce scade, această componentă crește uniform, datorită acțiunii g, accelerația gravitațională.
În ceea ce privește componenta orizontală a vitezei, aceasta rămâne constantă pe durata mișcării.
Conform celor menționate anterior, pozițiile sunt stabilite în funcție de timp, atât pe axa orizontală, cât și pe axa verticală. Direcția spre dreapta este luată ca axa + x, în timp ce direcția în jos este direcția -y. Valoarea gravitației este g = -9,8 m / sDouă sau -32 ft / sDouă:
x (t) = xsau + vbou.t (poziția orizontală); vbou este constant
y (t) = ysau + vHei.t - ½ g.tDouă (pozitie verticala); vDa = vHei - g.t (viteza verticală)
Poziția, viteza, timpul de zbor și intervalul orizontal maxim
Ecuațiile sunt simplificate prin alegerea următoarelor poziții de pornire: Xsau = 0, Dasau = 0 pe site-ul de lansare. Mai mult vHei = 0, întrucât mobilul este proiectat orizontal. Cu această alegere, ecuațiile mișcării sunt astfel:
x (t) = vbou.t; vX = vbou
y (t) = - ½ g.tDouă; vDa = - g.t
Când timpul nu este disponibil, este utilă ecuația referitoare la viteze și deplasări. Acest lucru este valabil pentru viteza verticală, deoarece orizontală rămâne constantă pe tot parcursul mișcării:
vDaDouă = vHeiDouă + 2.g .y = 2.g.y
Timp de zbor
Pentru a calcula timpul de zbor tzbor, să presupunem că mobilul este proiectat de la o înălțime H pe podea. Deoarece originea sistemului de referință a fost aleasă la punctul de lansare, atunci când ajunge la sol se află în poziție -H. Înlocuind acest lucru în ecuația 2) obținem:
-H = - ½ g.tDouăzbor
tzbor = (2H / g)½
Acoperire maximă
acoperire orizontală se obține prin înlocuirea acestui timp în x (t):
Xmax = vbou. (2H / g)½
Exerciții rezolvate
-Exercițiu rezolvat 1
Un elicopter zboară orizontal, menținând o înălțime constantă de 580 m când aruncă o cutie care conține alimente peste o tabără de refugiați. Cutia aterizează la o distanță orizontală de 150 m față de punctul de lansare. Găsiți: a) Timpul de zbor al casetei.
b) Viteza elicopterului.
c) Cât de repede a atins cutia la sol??
Soluţie
a) Înălțimea H de la care se lasă mâncarea este H = 500 m. Cu aceste date, la înlocuire, obținem:
tzbor = (2H / g)½= (2 x 580 / 9,8) ½s = 10,9 s
b) Elicopterul poartă viteza orizontală inițială vbou a pachetului și întrucât una dintre date este Xmax:
Xmax = vbou. (2H / g)½ ® vbou = xmax / (2H / g)½= xmax / tzbor = 150 m / 10,9 s = 13,8 m / s
c) Viteza proiectilului în orice moment este:
vDa = -g.t = -9,8 m / sDouă x 10,9 s = -106,82 m / s = - 384,6 km / h
Semnul negativ indică faptul că mobilul se deplasează în jos.
-Exercițiu rezolvat 2
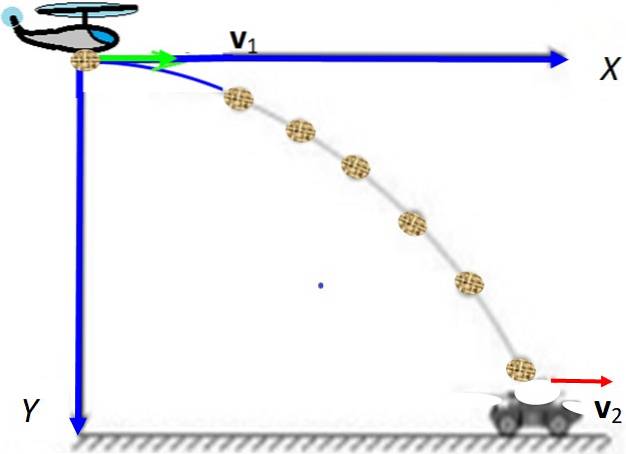
De la un avion care zboară orizontal la o înălțime H = 500 m Da 200 km / h un pachet cade și trebuie să cadă pe un vehicul deschis la care se deplasează 18 km / h pe drum. În ce poziție trebuie să cadă avionul pachetul astfel încât să cadă în vehicul? Nu luați în considerare rezistența aerului sau viteza vântului.
Soluţie
Este convenabil să treci mai întâi toate unitățile către sistemul internațional:
18 km / h = 6 m / s
200 km / h = 55 m / s
Există două dispozitive mobile: avion (1) și vehicul (2) și este necesar să alegeți un sistem de coordonate pentru a le localiza pe amândouă. Este convenabil să o faceți la punctul de plecare al pachetului în avion. Pachetul este proiectat orizontal cu viteza pe care o transportă avionul: v1, în timp ce vehiculul se deplasează la vDouă presupus constant.
-Avion
Poziția inițială: x = 0; y = 0
Viteza inițială = v1 (orizontală)
Ecuații de poziție: y (t) = -½g.tDouă ; x (t) = v1.t
-Vehicul
Poziția inițială: x = 0, y = -H
Viteza inițială = vDouă (constant)
x (t) = xsau + vDouă. t
Durata zborului coletului este:
tzbor = (2H / g)½ = (2 × 500 / 9,8)½s = 10,1 s
În acest timp, pachetul a cunoscut o deplasare orizontală de:
Xmax = vbou . (2H / g)½= 55 m / s x 10,1 s = 556 m.
În acest timp, vehiculul s-a deplasat și orizontal:
x (t) = v1.t = 6 m / s x10,1 s = 60,6 m
Dacă avionul aruncă pachetul imediat când vede vehiculul trecând sub el, nu îl va face să cadă chiar în el. Pentru ca acest lucru să se întâmple, trebuie să îl aruncați mai în spate:
d = 556 m - 60,6 m = 495,4 m.
Referințe
- Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill. 74-84.
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 1. Cinematica. Editat de Douglas Figueroa (USB). 117 - 164.
- Mișcarea proiectilului. Recuperat de pe: phys.libretexts.org.
- Rex, A. 2011. Fundamentele fizicii. Pearson. 53-58.
- Tippens, P. 2011. Fizică: concepte și aplicații. Ediția a VII-a. McGraw Hill. 126-131.


Nimeni nu a comentat acest articol încă.