
Caracteristici de împușcare parabolică oblică, formule, ecuații, exemple
lovitură parabolică oblică este un caz particular de mișcare de cădere liberă în care viteza inițială a proiectilului formează un anumit unghi cu orizontală, rezultând o traiectorie parabolică.
Căderea liberă este un caz de mișcare cu accelerație constantă, în care accelerația este cea a gravitației, care îndreaptă întotdeauna vertical în jos și are o magnitudine de 9,8 m / s ^ 2. Nu depinde de masa proiectilului, așa cum a arătat Galileo Galilei în 1604.
Dacă viteza inițială a proiectilului este verticală, căderea liberă are o traiectorie dreaptă și verticală, dar dacă viteza inițială este oblică, atunci traiectoria căderii libere este o curbă parabolică, fapt demonstrat și de Galileo.
Exemple de mișcare parabolică sunt traiectoria unui baseball, glonțul tras dintr-un tun și jetul de apă care iese dintr-un furtun..
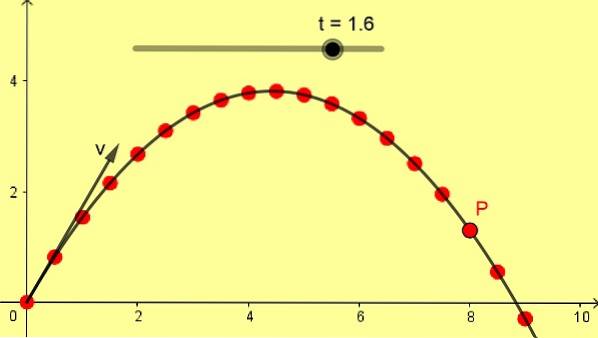
Figura 1 prezintă un curent parabolic oblic de 10 m / s cu un unghi de 60º. Scara este în metri și pozițiile succesive ale lui P sunt luate cu o diferență de 0,1 s începând de la momentul inițial 0 secunde.
Indice articol
- 1 Formule
- 1.1 Poziția și viteza
- 2 ecuații
- 2.1 Ecuații parametrice
- 2.2 Ecuația traiectoriei
- 3 Exemple
- 3.1 Exemplul 1
- 3.2 Exemplul 2
- 3.3 Exemplul 3
- 4 Referințe
Formule
Mișcarea unei particule este complet descrisă dacă poziția, viteza și accelerația acesteia sunt cunoscute ca o funcție a timpului..
Mișcarea parabolică rezultată dintr-o lovitură oblică este suprapunerea unei mișcări orizontale la viteză constantă, plus o mișcare verticală cu accelerație constantă egală cu accelerația gravitației..
Formulele care se aplică schiței parabolice oblic sunt cele care corespund unei mișcări cu accelerație constantă a = g, rețineți că a fost folosit bold pentru a indica faptul că accelerația este o mărime vectorială.
Poziție și viteză
Într-o mișcare cu accelerație constantă poziția depinde matematic de timp în formă pătratică.
Dacă denotăm r(t) poziția la timp t, rsau poziția la momentul inițial, vsau viteza initiala, g accelerare și t = 0 ca instant inițial formula care dă poziția pentru fiecare moment de timp t este:
r(t) = rsau + vsau t + ½ g tDouă
Grăsimea din expresia de mai sus indică faptul că este o ecuație vectorială.
Viteza în funcție de timp se obține luând derivata în raport cu t a poziției și rezultatul este:
v(t) = vsau + g t
Și pentru a obține accelerația în funcție de timp, derivata vitezei față de t rezultat:
la(t) = g
Când timpul nu este disponibil, există o relație între viteză și poziție, care este dată de:
vDouă = vsauDouă - 2 g (și - eu)
Ecuații
În continuare vom găsi ecuațiile care se aplică unei lovituri parabolice oblice în formă carteziană.
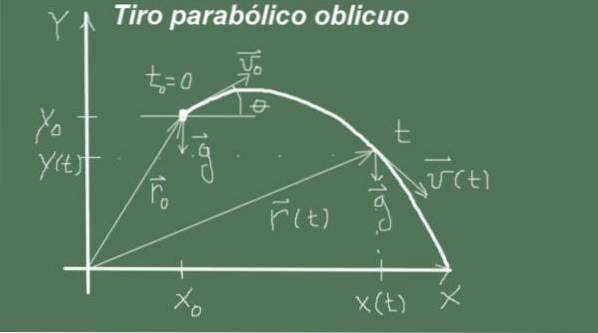
Mișcarea începe în clipa aceea t = 0 cu poziția de plecare (xo, eu) și viteza de mărime vsau și unghiul θ, adică vectorul vitezei inițiale este (vsau cosθ, vsau senθ). Mișcarea continuă cu accelerarea
g = (0, -g).
Ecuații parametrice
Dacă se aplică formula vectorială care dă poziția în funcție de timp și componentele sunt grupate și egalizate, atunci se vor obține ecuațiile care dau coordonatele poziției în orice moment al timpului t.
x (t) = xsau + vbou t
y (t) = ysau + vHei t-½ g tDouă
În mod similar, avem ecuațiile pentru componentele vitezei în funcție de timp.
vX(t) = vbou
vDa(t) = vHei - g t
Unde: vbou = vsau cosθ; vHei = vsau senθ
Ecuația traiectoriei
y = A x ^ 2 + B x + C
A = -g / (2 vbou^ 2)
B = (vHei/ vbou + g xsau/ vbou^ 2)
C = (șisau - vHei Xsau / vbou)
Exemple
Exemplul 1
Răspunde la următoarele întrebări:
a) De ce în problemele de tiraj parabolic este de obicei neglijat efectul fricțiunii cu aerul??
b) Are forma obiectului vreo importanță în împușcătura parabolică??
Răspunsuri
a) Pentru ca mișcarea unui proiectil să fie parabolică, este important ca forța de frecare a aerului să fie mult mai mică decât greutatea obiectului aruncat..
Dacă se aruncă o minge de plută sau un material ușor, forța de frecare este comparabilă cu greutatea și traiectoria sa nu se poate apropia de o parabolă.
Dimpotrivă, dacă este un obiect greu, cum ar fi o piatră, forța de frecare este neglijabilă în comparație cu greutatea pietrei și traiectoria ei se apropie de o parabolă..
b) Forma obiectului aruncat este de asemenea relevantă. Dacă o foaie de hârtie este aruncată sub forma unui avion, mișcarea acestuia nu va fi de cădere liberă sau parabolică, deoarece forma favorizează rezistența la aer.
Pe de altă parte, dacă aceeași foaie de hârtie este compactată într-o minge, mișcarea rezultată este foarte asemănătoare cu o parabolă.
Exemplul 2
Un proiectil este lansat de la sol orizontal cu o viteză de 10 m / s și un unghi de 60 °. Acestea sunt aceleași date cu care a fost elaborată figura 1. Cu aceste date, găsiți:
a) Moment în care atinge înălțimea maximă.
b) Înălțimea maximă.
c) Viteza la înălțimea maximă.
d) Poziția și viteza la 1,6 s.
e) În momentul în care lovește din nou pământul.
f) Atingerea orizontală.
Solutie la)
Viteza verticală în funcție de timp este
vDa(t) = vHei - g t = vsau sinθ - g t = 10 sin60º - 9,8 t = 8,66 - 9,8 t
În momentul în care se atinge înălțimea maximă, viteza verticală este zero pentru o clipă.
8,66 - 9,8 t = 0 ⇒ t = 0,88 s.
Soluția b)
Înălțimea maximă este dată de coordonată Da pentru momentul în care se atinge acea înălțime:
și (0,88s) = I + go t -½ g t ^Două = 0 + 8,66 * 0,88-½ 9,8 0,88 ^Două =
3,83 m
Prin urmare, înălțimea maximă este de 3,83 m.
Soluția c)
Viteza la înălțimea maximă este orizontală:
vX(t) = vbou = vsau cosθ = 10 cos60º = 5 m / s
Soluția d)
Poziția la 1,6 s este:
x (1,6) = 5 * 1,6 = 8,0 m
și (1.6) = 8,66 * 1,6-½ 9,8 1,6Două = 1,31 m
Soluția e)
Când coordonata y atinge solul, atunci:
y (t) = 8,66 * t-½ 9,8 tDouă = 0 ⇒ t = 1,77 s
Soluția f)
Atingerea orizontală este coordonata x exact în momentul în care atinge solul:
x (1,77) = 5 * 1,77 = 8,85 m
Exemplul 3
Găsiți ecuația traiectoriei cu datele din Exemplul 2.
Soluţie
Ecuația parametrică a căii este:
x (t) = 5 * t
y (t) = 8,66 * t-½ 9,8 t ^Două
Și ecuația carteziană se obține rezolvând t din prima și substituind în a doua
y = 8,66 * (x / 5) -½ 9,8 (x / 5) ^Două
Simplificând:
y = 1,73 x - 0,20 x ^ 2
Referințe
- P. P. Teodorescu (2007). "Cinematică". Sisteme mecanice, modele clasice: mecanica particulelor. Springer.
- Resnick, Halliday și Krane (2002). Fizica Volumul 1. Cecsa, Mexic.
- Thomas Wallace Wright (1896). Elemente de mecanică, inclusiv cinematică, cinetică și statică. E și FN Spon.
- Wikipedia. Mișcarea parabolică. Recuperat de pe es.wikipedia.org.
- Wikipedia. Mișcare de proiectil Recuperat de pe en.wikipedia.org.



Nimeni nu a comentat acest articol încă.