
Lucrare mecanică ce este, condiții, exemple, exerciții
munca mecanica Este definită ca schimbarea stării energetice a unui sistem, cauzată de acțiunea forțelor externe, cum ar fi gravitația sau fricțiunea. Unitățile de lucru mecanic din sistemul internațional (SI) sunt newton x metru sau jouli, prescurtate cu J.
Matematic este definit ca produsul scalar al vectorului de forță și al vectorului de deplasare. da F este forța constantă și l este deplasarea, ambii vectori, lucrarea W este exprimată ca: W = F ● l

Când forța nu este constantă, atunci trebuie să analizăm munca depusă atunci când deplasările sunt foarte mici sau diferențiale. În acest caz, dacă punctul A este considerat punctul de plecare și B ca punctul de sosire, lucrarea totală se obține prin adăugarea tuturor contribuțiilor la acesta. Acest lucru este echivalent cu calcularea următoarei integrale:
Variația în energie a sistemului = Munca efectuată de forțe externe
ΔE = Wext
Când se adaugă energie la sistem, W> 0 și când se scade energia W<0. Ahora bien, si ΔE = 0, puede significar que:
-Sistemul este izolat și nu există forțe externe care acționează asupra acestuia.
-Există forțe externe, dar nu lucrează la sistem.
Deoarece schimbarea energiei este egală cu munca efectuată de forțe externe, unitatea SI de energie este, de asemenea, joul. Aceasta include orice tip de energie: cinetică, potențială, termică, chimică și multe altele..
Indice articol
- 1 Condiții pentru a exista lucrări mecanice
- 1.1 Semne de lucru
- 2 Exemple de lucru mecanic
- 3 Teorema de lucru-energie cinetică
- 3.1 Lucrări efectuate pentru întinderea unui arc
- 4 Exerciții
- 4.1 Exercițiul 1
- 4.2 Exercițiul 2
- 5 Referințe
Condiții pentru a exista lucrări mecanice
Am văzut deja că munca este definită ca un produs dot. Să luăm definiția muncii efectuate de o forță constantă și să aplicăm conceptul de produs punct între doi vectori:
W = F ● l = F.l.cos θ
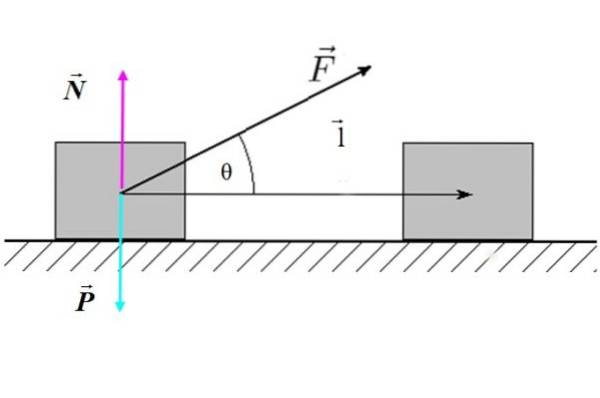
Unde F este magnitudinea forței, l este magnitudinea deplasării și θ este unghiul dintre forță și deplasare. În figura 2 există un exemplu de forță externă înclinată care acționează asupra unui bloc (sistemul), care produce o deplasare orizontală.

Rescrierea lucrării după cum urmează:
W = (F. cos θ). l
Putem afirma că numai componenta forței paralele cu deplasarea: F. cos θ ee capabil să facă treabă. Dacă θ = 90º atunci cos θ = 0 și lucrarea ar fi zero.
Prin urmare, se concluzionează că forțele perpendiculare pe deplasare nu fac lucrări mecanice.
În cazul figurii 2, nici forța normală N nici greutatea P funcționează, deoarece ambele sunt perpendiculare pe deplasare l.
Semnele muncii
Așa cum s-a explicat mai sus, W Poate fi pozitiv sau negativ. Când cos θ> 0, munca efectuată de forță este pozitivă, deoarece are aceeași direcție de mișcare.
da cos θ = 1, forța și deplasarea sunt paralele și munca este maximă.
În cazul cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.
Cand cos θ = -1, forța este complet opusă deplasării, cum ar fi fricțiunea cinetică, al cărei efect este de a încetini obiectul asupra căruia acționează. Deci munca este minimă.
Acest lucru este de acord cu ceea ce s-a spus la început: dacă lucrarea este pozitivă, se adaugă energie la sistem, iar dacă este negativă, se scade.
Muncă netă Wnet Este definit ca suma muncii efectuate de toate forțele care acționează asupra sistemului:
Wnet = ∑Weu
Apoi putem concluziona că pentru a garanta existența unei lucrări mecanice nete este necesar ca:
-Forțele externe acționează asupra obiectului.
-Aceste forțe nu sunt toate perpendiculare pe deplasare (cos θ ≠ 0).
-Lucrările efectuate de fiecare forță nu se anulează reciproc.
-Există o deplasare.
Exemple de lucru mecanic
-Ori de câte ori este necesar să puneți un obiect în mișcare din repaus, este necesar să faceți lucrări mecanice. De exemplu, împingerea unui frigider sau a unui portbagaj greu pe o suprafață orizontală.
-Un alt exemplu de situație în care trebuie să faceți lucrări mecanice este schimbarea vitezei unei mingi în mișcare..
-Este necesar să se lucreze pentru a ridica un obiect la o anumită înălțime deasupra podelei.
Acum, există situații la fel de frecvente în care nu munca se face, chiar dacă aparențele indică contrariul. Am spus că pentru a ridica un obiect la o anumită înălțime trebuie să lucrați, așa că purtăm obiectul, îl ridicăm deasupra capului și îl ținem acolo. Facem treabă?
Se pare că da, pentru că dacă obiectul este greu, brațele se vor obosi într-un timp scurt, totuși, oricât de greu ar fi, nu se lucrează din punct de vedere al Fizicii. De ce nu? Ei bine, pentru că obiectul nu se mișcă.
Un alt caz în care, deși are o forță externă, nu efectuează lucrări mecanice este atunci când particula are o mișcare circulară uniformă.
De exemplu, un copil care învârte o piatră legată de un șnur. Tensiunea șirului este forța centripetă care permite rotirea pietrei. Dar în orice moment această forță este perpendiculară pe deplasare. Apoi nu efectuează lucrări mecanice, deși favorizează mișcarea.
Teorema muncii-energiei cinetice
Energia cinetică a sistemului este cea pe care o posedă în virtutea mișcării sale. da m este masa și v este viteza de mișcare, energia cinetică este notată cu K și este dat de:
K = ½ mvDouă
Prin definiție, energia cinetică a unui obiect nu poate fi negativă, deoarece atât masa cât și pătratul vitezei sunt întotdeauna cantități pozitive. Energia cinetică poate fi 0, atunci când obiectul este în repaus.
Pentru a schimba energia cinetică a unui sistem, este necesar să-i variați viteza - vom considera că masa rămâne constantă, deși acest lucru nu este întotdeauna cazul. Acest lucru necesită o muncă netă a sistemului, prin urmare:
Wnet = ΔK
Aceasta este teorema muncii - energia cinetică. Se afirmă că:
Munca netă este egală cu schimbarea energiei cinetice a sistemului
Rețineți că, deși K este întotdeauna pozitiv, ΔK poate fi pozitiv sau negativ, deoarece:
ΔK = Kfinal - K iniţială
da Kfinal >K iniţială sistemul a câștigat energie și ΔK> 0. Dimpotrivă, dacă Kfinal < K iniţială, sistemul a renunțat la putere.
Lucrare făcută pentru a întinde un arc
Când un arc este întins (sau comprimat), trebuie să se lucreze. Această lucrare este stocată în primăvară, permițându-i, la rândul său, să lucreze la, să zicem, un bloc care este atașat la unul dintre capetele sale..
Legea lui Hooke afirmă că forța exercitată de un arc este o forță de refacere - este contrară deplasării - și, de asemenea, proporțională cu deplasarea menționată. Constanta de proporționalitate depinde de modul în care este arcul: moale și ușor de deformabil sau rigid.
Această forță este dată de:
Fr = -kx
În expresie, Fr este forța, k este constanta arcului și X este deplasarea. Semnul negativ indică faptul că forța exercitată de arc se opune deplasării.
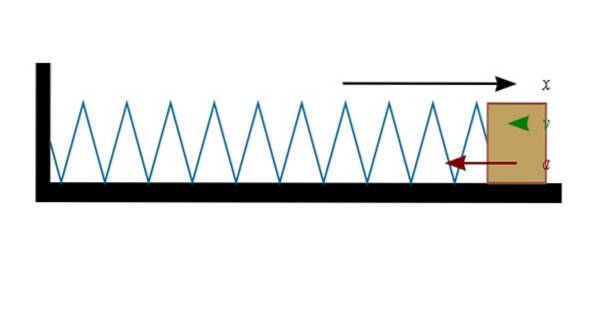
Dacă arcul este comprimat (spre stânga în figură), blocul de la capătul său se va deplasa spre dreapta. Și când arcul este întins (spre dreapta), blocul va dori să se deplaseze spre stânga.
Pentru a comprima sau întinde arcul, un agent extern trebuie să facă lucrarea și, deoarece este o forță variabilă, pentru a calcula lucrarea menționată, trebuie să folosim definiția dată la început:
Este foarte important să rețineți că aceasta este munca efectuată de agentul extern (mâna unei persoane, de exemplu) pentru comprimarea sau întinderea arcului. De aceea semnul negativ nu apare. Și întrucât pozițiile sunt pătrate, nu contează dacă sunt compresii sau întinderi..
Lucrarea pe care o va face la rândul său arc la bloc este:
Warc = -Wext
Instruire
Exercitiul 1
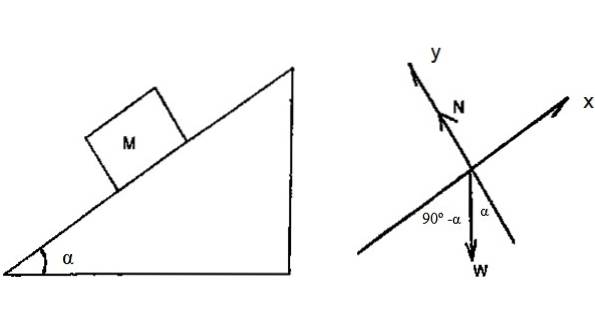
Blocul din figura 4 are masa M = 2 kg și alunecă în jos pe planul înclinat fără frecare, cu α = 36,9º. Presupunând că este permis să alunece din odihnă din vârful planului, a cărui înălțime este h = 3 m, găsiți viteza cu care blocul ajunge la baza planului, folosind teorema de lucru a energiei cinetice.

Soluţie
Diagrama corpului liber arată că singura forță capabilă să lucreze pe bloc este greutatea. Mai precis: componenta greutății de-a lungul axei x.
Distanța parcursă de blocul din plan se calculează folosind trigonometria:
d = 3 / (cos 36,9º) m = 3,75 m
Wgreutate = (Mg). d. cos (90-α) = 2 x 9,8 x 3,75 x cos 53,1 º J = 44,1 J
Prin teorema muncii-energie cinetică:
Wnet = ΔK
Wnet = Wgreutate
ΔK = ½ MvFDouă- ½ MvsauDouă
De vreme ce este eliberat din odihnă, vsau = 0, Prin urmare:
Wnet = ½ MvFDouă

Exercițiul 2
Un arc orizontal, a cărui constantă este k = 750 N / m, este fixat la un capăt de un perete. O persoană comprimă celălalt capăt la o distanță de 5 cm. Calculați: a) Forța exercitată de persoană, b) Munca pe care a făcut-o pentru comprimarea arcului.
Soluţie
a) Mărimea forței aplicate de persoană este:
F = kx = 750 N / m. 5x10 -Două m = 37,5 N.
b) Dacă sfârșitul arcului este inițial la x1 = 0, pentru ao duce de acolo la poziția finală xDouă = 5 cm, este necesar să efectuați următoarea lucrare, în funcție de rezultatul obținut în secțiunea anterioară:
Wext = ½ k (xDouăDouă - X1Două) = 0,5 x 750 x (0,05Două -0Două) J = 0,9375 J.
Referințe
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 2. Dinamica. Editat de Douglas Figueroa (USB).
- Iparraguirre, L. 2009. Mecanică de bază. Colecția Științe ale naturii și matematică. Distribuție online gratuită.
- Knight, R. 2017. Fizica pentru oamenii de știință și inginerie: o abordare strategică. Pearson.
- Libretexturi de fizică. Teorema muncii-energie. Recuperat de pe: phys.libretexts.org
- Muncă și energie. Recuperat de la: physics.bu.edu
- Muncă, energie și putere. Adus de la: ncert.nic.in


Nimeni nu a comentat acest articol încă.