Proprietăți trapezoidale isoscele, relații și formule, exemple

A trapez isoscel este un patrulater în care două dintre laturi sunt paralele între ele și, de asemenea, cele două unghiuri adiacente uneia dintre aceste laturi paralele au aceeași măsură.

În figura 1 avem patrulaterul ABCD, în care laturile AD și BC sunt paralele. În plus, unghiurile ∠DAB și ∠ADC adiacente laturii paralele AD au aceeași măsură α. 

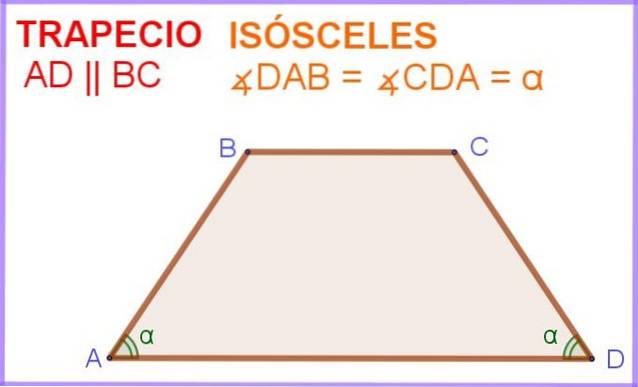
Deci, acest patrulater, sau poligon cu patru fețe, este de fapt un trapez isoscel.

Într-un trapez, se numesc laturile paralele baze iar nonparalelele sunt numite lateral. O altă caracteristică importantă este înălţime, care este distanța care separă laturile paralele.

În plus față de trapezul isoscel există și alte tipuri de trapez:

-Tmustar scalen, care are toate unghiurile și laturile sale diferite.

-Tdreptunghiular pescar, în care un lateral are unghiuri adiacente drepte.

Forma trapezoidală este comună în diferite domenii de proiectare, arhitectură, electronică, calcul și multe altele, așa cum se va vedea mai târziu. De aici și importanța familiarizării cu proprietățile sale.

Indice articol

• 1 Proprietăți
  • 1.1 Exclusivele trapezului isoscel
  • 1.2 Pentru toate trapezele
• 2 Relații și formule
  • 2.1 Relații unice ale trapezului isoscel
  • 2.2 Relații pentru orice trapez
  • 2.3 Relații pentru trapez isoscel cu circumferință inscripționată
  • 2.4 Formule pentru determinarea unei laturi, cunoașterea celorlalte și un unghi
  • 2.5 Determinarea unei laturi, cunoașterea celorlalte și a unei diagonale
  • 2.6 Baza de la înălțime, zonă și altă bază
  • 2.7 Bazele laterale, aria și unghiul cunoscute
  • 2.8 Mediană laterală, zonă și unghi cunoscute
  • 2.9 Înălțimea cunoscută a laturilor
  • 2.10 Înălțimea cunoscută, un unghi și două laturi
  • 2.11 Diagonalele cunoscute pe toate laturile, sau pe două laturi și un unghi
  • 2.12 Perimetrul triunghiului isoscel 
  • 2.13 Aria trapezului izoscel
  • 2.14 Raza cercului circumscris
• 3 Exemple de utilizare a trapezului isoscel
  • 3.1 În arhitectură și construcții
  • 3.2 În proiectare
• 4 exerciții rezolvate
  • 4.1 - Exercițiul 1
  • 4.2 - Exercițiul 2
• 5 Referințe

Proprietăți

Exclusiv pentru trapezul isoscel

Dacă un trapez este isoscel atunci are următoarele proprietăți caracteristice:

1.- Părțile au aceeași măsurare.

2.- Unghiurile adiacente bazelor sunt egale.

3.- Unghiurile opuse sunt suplimentare.

4.- Diagonalele au aceeași lungime, cele două segmente care unesc vârfurile opuse fiind aceleași.

5.- Unghiul format între baze și diagonale sunt toate de aceeași măsură.

6.- Are o circumferință circumscrisă.

În schimb, dacă un trapez îndeplinește oricare dintre proprietățile de mai sus, atunci este un trapez isoscel.

Dacă într-un trapez isoscel unul dintre unghiuri este drept (90º), atunci și celelalte unghiuri vor fi drepte, formând un dreptunghi. Adică, un dreptunghi este un caz particular al trapezului isoscel.

Pentru toate trapezele

Următorul set de proprietăți este valabil pentru orice trapez:

7.- The median a trapezului, adică segmentul care unește punctele medii ale laturilor sale ne paralele, este paralel cu oricare dintre baze.

8.- Lungimea medianei este egală cu semi-suma (suma împărțită la 2) din cea a bazelor sale.

9.- Mediana unui trapez își taie diagonalele în punctul mediu.

10.- Diagonalele unui trapez se intersectează într-un punct care le împarte în două secțiuni proporționale cu coeficienții bazelor.

11.- Suma pătratelor diagonalelor unui trapez este egală cu suma pătratelor laturilor sale plus produsul dublu al bazelor sale.

12.- Segmentul care unește punctele medii ale diagonalelor are o lungime egală cu semidiferența bazelor.

13.- Unghiurile adiacente celor laterale sunt suplimentare.

14.- Un trapez are o circumferință inscripționată dacă și numai dacă suma bazelor sale este egală cu suma laturilor sale.

15.- Dacă un trapez are o circumferință inscripționată, atunci unghiurile cu un vârf în centrul circumferinței menționate și laturile care trec prin capetele aceleiași părți sunt unghiuri drepte.

Relații și formule

Următorul set de relații și formule se referă la figura 3, unde pe lângă trapezul isoscel sunt prezentate și alte segmente importante deja menționate, cum ar fi diagonalele, înălțimea și mediana.

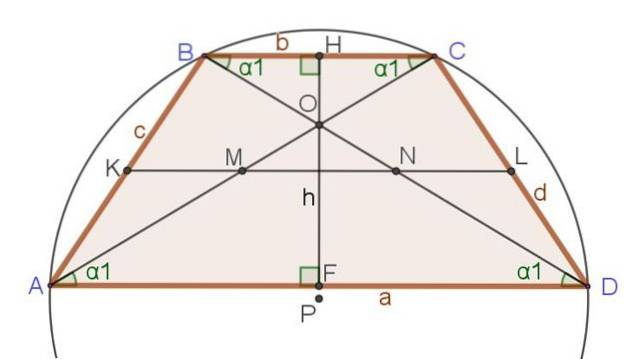
Relații unice ale trapezului isoscel

1.- AB = DC = c = d

2.- ∡DAB = ∡CDA și ∡ABC = ∡BCD

3.- ∡DAB + ∡BCD = 180º și ∡CDA + ∡ABC = 180º

4.- BD = AC

5.- ∡CAD = ∡BDA = ∡CBD = ∡BCA = α₁

6.- A, B, C și D aparțin cercului circumscris.

Relații pentru orice trapez

7. Dacă AK = KB și DL = LC ⇒ KL || AD și KL || Î.Hr.

8.- KL = (AD + BC) / 2

9.- AM = MC = AC / 2 și DN = NB = DB / 2

10.- AO / OC = AD / BC și DO / OB = AD / BC

11.- AC^Două + DB^Două = AB^Două + DC^Două + 2⋅AD⋅BC

12.- MN = (AD - BC) / 2

13.- ∡DAB + ∡ABC = 180º și ∡CDA + ∡BCD = 180º

14.- Dacă AD + BC = AB + DC ⇒ ∃ R decât echidistant de la AD, BC, AB și DC

15.- Dacă ∃ R echidistant de AD, BC, AB și DC, atunci:

∡BRA = ∡DRC = 90º

Relații pentru trapez isoscel cu circumferință inscripționată

Dacă într-un trapez isoscel suma bazelor este egală cu de două ori una laterală, atunci există circumferința înscrisă.

Următoarele proprietăți se aplică atunci când trapezul isoscel are o circumferință inscripționată (a se vedea figura 4 de mai sus):

16.- KL = AB = DC = (AD + BC) / 2

17.- Diagonalele se intersectează în unghi drept: AC ⊥ BD

18.- Înălțimea măsoară la fel ca mediana: HF = KL, adică h = m.

19.- Pătratul înălțimii este egal cu produsul bazelor: h^Două = BC⋅AD

20.- În aceste condiții specifice, aria trapezului este egală cu pătratul înălțimii sau produsul bazelor: Suprafața = h^Două = BC⋅AD.

Formule pentru determinarea unei părți, cunoașterea celorlalte și un unghi

Cunoscută o bază, laterala și un unghi, cealaltă bază poate fi determinată de:

a = b + 2c Cos α

b = a - 2c Cos α

Dacă lungimea bazelor și un unghi sunt date ca date cunoscute, atunci lungimile ambelor părți sunt:

c = (a - b) / (2 Cos α)

Determinarea unei laturi, cunoașterea celorlalte și a unei diagonale

a = (d₁^Două - c^Două) / b;

b = (d₁^Două - c^Două)/ la 

c = √ (d₁^Două - a⋅b)

Unde D₁ este lungimea diagonalelor.

Baza de la înălțime, zonă și altă bază

a = (2 A) / h - b

b = (2 A) / h - a

Bazele laterale, zona și unghiul cunoscute

c = (2A) / [(a + b) sin α]

Mediană laterală, zonă și unghi cunoscute

c = A / (m sin α)

Înălțimea cunoscută a laturilor

h = √ [4 c^Două - (a - b)^Două]

Înălțime cunoscută un unghi și două laturi

h = tg α⋅ (a - b) / 2 = c. sin α

Diagonalele cunoscute pe toate laturile, sau pe două laturi și un unghi

d₁ = √ (c^Două+ a b)

d₁ = √ (a^Două+ c^Două - 2 a c Cos α)

d₁ = √ (b^Două + c^Două- 2 b c Cos β)

Perimetrul triunghiului isoscel 

P = a + b + 2c

Zona trapezului isoscel

Există mai multe formule pentru calcularea zonei, în funcție de datele cunoscute. Următorul este cel mai cunoscut, în funcție de baze și înălțime:

A = h⋅ (a + b) / 2

Și le puteți folosi și pe acestea:

-Dacă laturile sunt cunoscute

A = [(a + b) / 4] √ [4c^Două - (a - b)^Două]

-Când ai două laturi și un unghi

A = (b + c Cos α) c Sen α = (a - c Cos α) c Sen α

-Dacă se cunoaște raza cercului înscris și un unghi

A = 4 r^Două / Sen α = 4 r^Două / Sen β

-Când se cunosc bazele și un unghi

A = a⋅b / Sen α = a⋅b / Sen β 

-Dacă trapezul poate fi înscris o circumferință

A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b) / 2

-Cunoscute diagonalele și unghiul pe care le formează între ele

A = (d₁^Două/ 2) Sen γ = (d₁^Două / 2) Sen δ 

-Când aveți lateralul, mediana și un unghi

A = mc.sen α = mc.sen β

Raza cercului circumscris

Doar trapezele izoscele au circumferință circumscrisă. Dacă baza mai mare a, c laterală și diagonala d sunt cunoscute₁, atunci raza R a cercului care trece prin cele patru vârfuri ale trapezului este:

R = a⋅c⋅d₁ / 4√ [p (p -a) (p -c) (p - d₁)]]

Unde p = (a + c + d₁) / Două

Exemple de utilizare a trapezului isoscel

Trapezul isoscel apare în câmpul de proiectare, așa cum se vede în Figura 2. Iată câteva exemple suplimentare:

În arhitectură și construcții

Vechiul inca știa trapezul isoscel și l-a folosit ca element de construcție în această fereastră din Cuzco, Peru:

Și aici trapezul apare din nou în apel foaie trapezoidală, un material utilizat frecvent în construcții:

În design

Am văzut deja că trapezul isoscel apare în obiecte de zi cu zi, inclusiv în alimente precum această batonă de ciocolată:

Exerciții rezolvate

- Exercitiul 1

Un trapez isoscel are o bază mai mare de 9 cm, o bază mai mică de 3 cm, iar diagonalele sale de 8 cm fiecare. Calculati:

a) Partea

b) Înălțime

c) Perimetrul

d) Zona

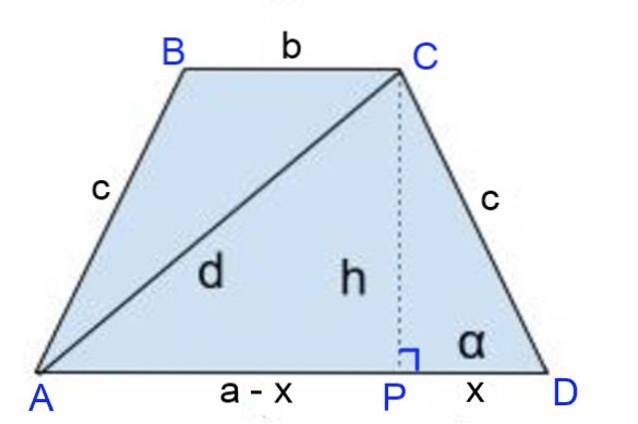
Solutie la

Înălțimea CP = h este reprezentată grafic, unde piciorul înălțimii definește segmentele:

PD = x = (a-b) / 2 y 

AP = a - x = a - a / 2 + b / 2 = (a + b) / 2.

Folosind teorema lui Pitagora la triunghiul dreptunghi DPC:

c^Două = h^Două + (a - b)^Două / 4

Și, de asemenea, în triunghiul dreptunghiular APC:

d^Două = h^Două + AP^Două = h^Două + (a + b)^Două / 4

În cele din urmă, membru cu membru, a doua ecuație este scăzută din prima și simplificată:

d^Două - c^Două = ¼ [(a + b)^Două - (a-b)^Două] = ¼ [(a + b + a-b) (a + b-a + b)]

d^Două - c^Două = ¼ [2a 2b] = a b

c^Două= d^Două - a b ⇒ c = √ (d^Două - a b) = √ (8^Două - 9⋅3) = √37 = 6,08 cm

Soluția b

h^Două = d^Două - (a + b)^Două / 4 = 8^Două - (12^Două / Două^Două ) = 8^Două - 6^Două = 28

h = 2 √7 = 5,29 cm

Soluția c

Perimetru = a + b + 2 c = 9 + 3 + 2⋅6.083 = 24.166 cm

Soluția d

Suprafață = h (a + b) / 2 = 5,29 (12) / 2 = 31,74 cm

- Exercițiul 2

Există un trapez isoscel a cărui bază cea mai mare este de două ori mai mică și cea mai mică bază este egală cu înălțimea, care este de 6 cm. Decide:

a) Lungimea lateralului

b) Perimetrul

c) Zona

d) Unghiuri

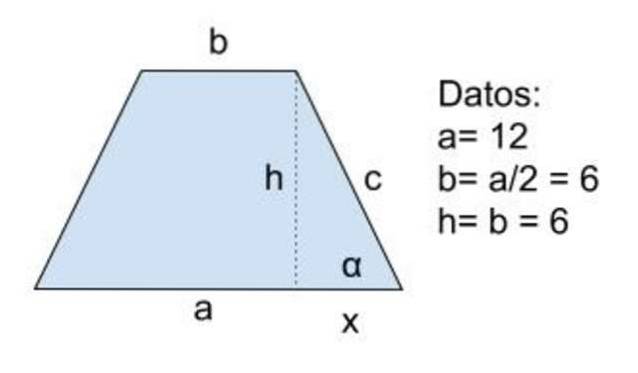
Solutie la

Date: a = 12, b = a / 2 = 6 și h = b = 6

Procedăm în acest fel: înălțimea h este trasată și teorema pitagoreică se aplică triunghiului hipotenuzei „c” și picioarelor h și x:

c^Două = h^Două+xc^Două

Apoi, trebuie să calculați valoarea înălțimii din datele (h = b) și cea a piciorului x: 

a = b + 2 x ⇒ x = (a-b) / 2

Înlocuind expresiile anterioare avem:

c^Două = b^Două+(a-b)^Două/Două^Două

Acum sunt introduse valorile numerice și se simplifică:

c^Două = 62+ (12-6) 2/4

c^Două = 62 (1 + ¼) = 62 (5/4)

Obținerea:

c = 3√5 = 6,71 cm

Soluția b

Perimetrul P = a + b + 2 c

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm

Soluția c

Zona în funcție de înălțimea și lungimea bazelor este:

A = h⋅ (a + b) / 2 = 6⋅ (12 + 6) / 2 = 54 cm^Două

Soluția d

Unghiul α format de lateral cu baza mai mare se obține prin trigonometrie:

Tan (α) = h / x = 6/3 = 2

α = ArcTan (2) = 63,44º

Celălalt unghi, cel care formează lateralul cu baza mai mică, este β, care este suplimentar față de α:

β = 180º - α = 180º - 63,44º = 116,56º

Referințe

1. E. A. 2003. Elemente de geometrie: cu exerciții și geometrie a busolei. Universitatea din Medellin.
2. Campos, F. 2014. Matematică 2. Grupo Editorial Patria.
3. Eliberat, K. 2007. Descoperă poligoanele. Benchmark Education Company.
4. Hendrik, V. 2013. Poligoane generalizate. Birkhäuser.
5. IGER. Matematică Primul semestru Tacaná. IGER.
6. Jr. geometrie. 2014. Poligoane. Lulu Press, Inc..
7. Miller, Heeren și Hornsby. 2006. Matematică: raționament și aplicații. Al 10-lea. Ediție. Pearson Education.
8. Patiño, M. 2006. Matematică 5. Editorial Progreso.
9. Wikipedia. Trapez. Recuperat de pe: es.wikipedia.com