
Triunghiuri istorice, elemente, clasificare, proprietăți

triunghiuri Sunt figuri geometrice plate și închise, formate din trei laturi. Un triunghi este determinat de trei linii care se intersectează două câte două, formând trei unghiuri între ele. Forma triunghiulară, plină de simbolism, este prezentă în nenumărate obiecte și ca element de construcție.
Originea triunghiului se pierde în istorie. Din dovezile arheologice se știe că omenirea primitivă o știa bine, deoarece rămășițele arheologice confirmă că a fost folosită în unelte și arme.

Este, de asemenea, clar că vechii egipteni aveau o cunoaștere solidă a geometriei și în special a formei triunghiulare. Ele s-au reflectat în elementele arhitecturale ale clădirilor sale monumentale.
În papirusul Rhind sunt formule pentru calcularea ariilor de triunghiuri și trapezoide, precum și unele volume și alte concepte de trigonometrie rudimentară.
La rândul lor, se știe că babilonienii au fost capabili să calculeze aria triunghiului și a altor figuri geometrice, pe care le-au folosit în scopuri practice, cum ar fi diviziunile de terenuri. De asemenea, aveau cunoștințe despre multe proprietăți ale triunghiurilor.
Cu toate acestea, grecii antici au fost cei care au sistematizat multe dintre conceptele geometrice predominante astăzi, deși o mare parte din aceste cunoștințe nu erau exclusive, deoarece erau cu siguranță împărtășite cu aceste alte civilizații antice..
Indice articol
- 1 Elemente ale triunghiului
- 1.1 Notare
- 2 Tipuri de triunghiuri
- 2.1 Congruența triunghiurilor
- 2.2 Asemănarea triunghiurilor
- 3 Proprietăți
- 4 Teoreme
- 4.1 Prima teoremă a lui Thales
- 4.2 A doua teoremă a lui Thales
- 4.3 Teorema lui Pitagora
- 5 Aria unui triunghi
- 6 Exemple de triunghiuri
- 6.1 Exemplul 1
- 6.2 Exemplul 2
- 6.3 Exemplul 3
- 7 Exerciții
- 7.1 Exercițiul 1
- 7.2 Exercițiul 2
- 8 Referințe
Elemente de triunghi
Elementele oricărui triunghi sunt indicate în figura următoare. Există trei: vârfuri, laturi și unghiuri.
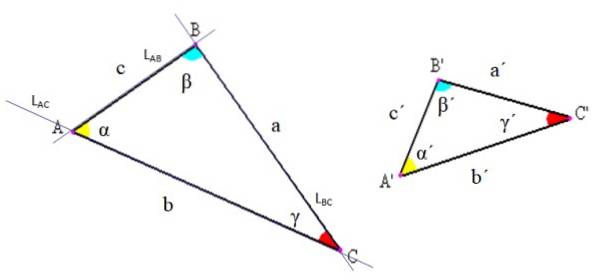
-Vârfuri: sunt punctele de intersecție ale liniilor ale căror segmente determină triunghiul. În figura de mai sus, de exemplu, linia LAC care conține segmentul AC, intersectează linia LAB care conține segmentul AB chiar în punctul A.
-Părțile laterale: între fiecare pereche de vârfuri se trasează un segment de linie care constituie o parte a triunghiului. Acest segment poate fi notat cu literele de final sau folosind o anumită literă pentru a-l apela. În exemplul din figura 2, latura AB se mai numește „c”.
-Unghiuri: Între fiecare parte cu un vârf comun își are originea un unghi, al cărui vârf coincide cu cel al triunghiului. În general, unghiul este notat cu o literă greacă, așa cum se spunea la început.
Pentru a construi un anumit triunghi, cu o formă și dimensiune date, trebuie doar să aveți unul dintre următoarele seturi de date:
-Toate cele trei laturi, destul de evident pentru un triunghi.
-Două laturi și unghiul dintre ele și imediat se trasează partea rămasă.
-Două unghiuri (interne) și latura dintre ele. Prin extensie se desenează cele două laturi lipsă și triunghiul este gata.
Notaţie
În general, în notația triunghiului se utilizează următoarele convenții: vârfurile sunt indicate cu litere latine majuscule, laturile cu litere latine minuscule și unghiurile cu litere grecești (vezi figura 2).
În acest fel triunghiul este numit în funcție de vârfurile sale. De exemplu, triunghiul din stânga din figura 2 este triunghiul ABC, iar cel din dreapta este triunghiul A'B'C '.
De asemenea, este posibil să utilizați alte notații; de exemplu, unghiul α din figura 2 este notat ca BAC. Rețineți că litera vârfului merge în mijloc, iar literele sunt scrise în sens invers acelor de ceasornic.
Alteori este plasat un cursor pentru a indica unghiul:
α = ∠A
Tipuri de triunghiuri
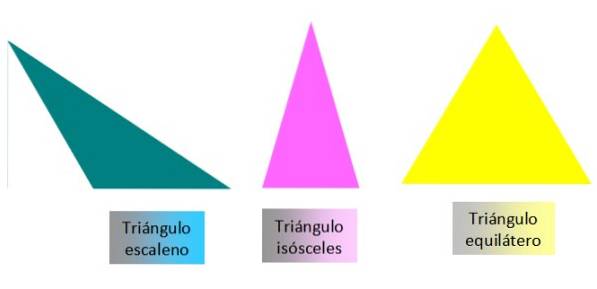
Există mai multe criterii pentru clasificarea triunghiurilor. Cel mai obișnuit este să le clasificăm după măsura laturilor lor sau după măsura unghiurilor lor. În funcție de măsura laturilor lor, triunghiurile pot fi: scalene, isoscel sau echilaterale:
-Scalen: cele trei laturi ale sale sunt diferite.
-Isoscel: are două laturi egale și una laterală diferită.
-Echilateral: toate cele trei laturi sunt egale.

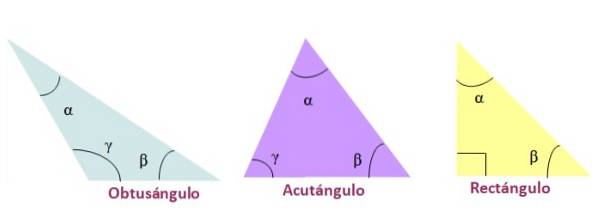
În funcție de măsura unghiurilor lor, triunghiurile sunt numite astfel:
-Unghi obtuz, dacă unul dintre unghiurile interne este mai mare de 90º.
-Unghi ascutit, când cele trei unghiuri interne ale triunghiului sunt acute, adică mai puțin de 90º
-Dreptunghi, în cazul în care unul dintre unghiurile sale interne este de 90º. Laturile care formează 90º se numesc picioare, iar latura opusă unghiului drept este hipotenuza..
Congruența triunghiurilor
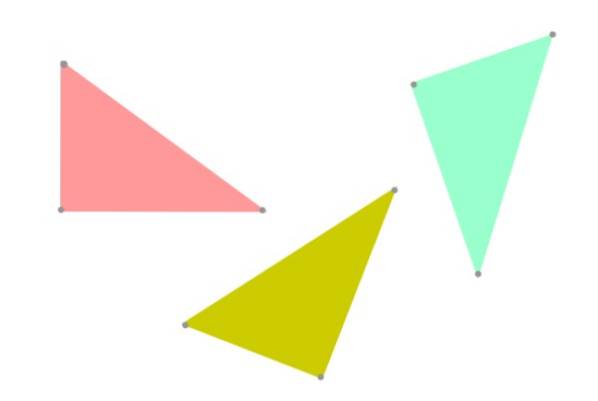
Când două triunghiuri au aceeași formă și au aceeași dimensiune, se spune că sunt congruente. Desigur, congruența este legată de egalitate, așa că de ce în geometrie vorbim de „două triunghiuri congruente” în loc de „două triunghiuri egale”?
Ei bine, este preferabil să folosiți termenul „congruență” pentru a rămâne la adevăr, deoarece două triunghiuri pot avea aceeași formă și dimensiune, dar pot fi orientate diferit în plan (a se vedea figura 3). Din punct de vedere al geometriei, acestea nu ar mai fi strict la fel.
Criterii de congruență
Două triunghiuri sunt congruente dacă apare oricare dintre următoarele:
-Toate cele trei părți măsoară la fel (din nou acesta este cel mai evident).
-Au două laturi identice și cu același unghi între ele.
-Ambele au două unghiuri interne identice, iar latura dintre aceste unghiuri măsoară la fel.
După cum se poate vedea, este vorba despre cele două triunghiuri care îndeplinesc condițiile necesare pentru ca atunci când sunt construite, forma și dimensiunea lor să fie exact aceleași..
Criteriile de congruență sunt foarte utile, deoarece, în practică, nenumărate piese și piese mecanice trebuie fabricate în serie, astfel încât măsurătorile și forma lor să fie exact aceleași.
Asemănarea triunghiurilor
Un triunghi este similar cu altul dacă au aceeași formă, chiar dacă sunt de dimensiuni diferite. Pentru a vă asigura că forma este aceeași, este necesar ca unghiurile interne să aibă aceeași valoare și ca laturile să fie proporționale..
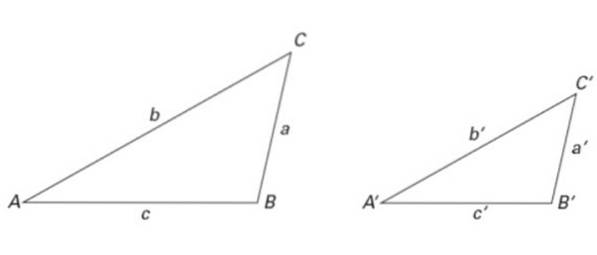
Triunghiurile din figura 2 sunt, de asemenea, similare, la fel ca cele din figura 6. În acest fel:
∠ A = ∠ A ', ∠ B = ∠ B 'și ∠ C = ∠ C '
În ceea ce privește laturile, sunt valabile următoarele rapoarte de similaritate:
a / a '= b / b' = c / c '
Proprietăți
Proprietățile fundamentale ale triunghiurilor sunt următoarele:
-Suma unghiurilor interioare ale oricărui triunghi este întotdeauna de 180º.
-Pentru orice triunghi, suma unghiurilor sale exterioare este egală cu 360 °.
- Un unghi extern al unui triunghi este egal cu suma celor două unghiuri interioare care nu sunt adiacente unghiului menționat.
Teoreme
Prima teoremă a lui Thales
Acestea sunt atribuite filosofului și matematicianului grec Thales din Milet, care a dezvoltat mai multe teoreme legate de geometrie. Primul dintre ele stabilește următoarele:
Dacă mai multe linii paralele intersectează două linii transversale, în ele se determină segmente proporționale.
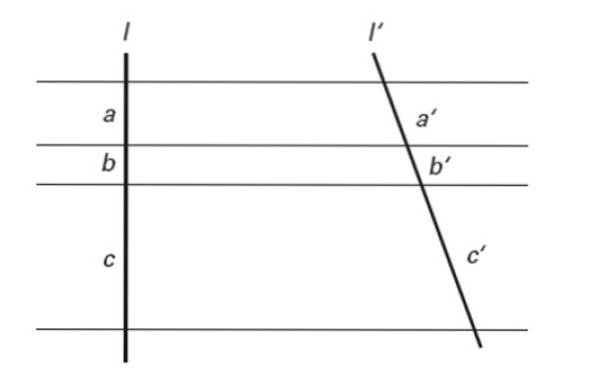
Cu alte cuvinte:
a / a '= b / b' = c / c '
Prima teoremă a lui Thales se aplică unui triunghi, de exemplu avem triunghiul albastru ABC în stânga, care este tăiat de paralelele roșii din dreapta:
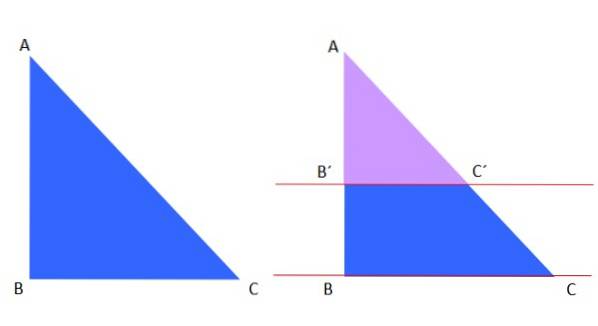
Triunghiul violet AB'C 'este similar cu triunghiul albastru ABC, prin urmare, conform teoremei lui Thales, se pot scrie următoarele:
AB '/ AC' = AB / AC
Și este în concordanță cu ceea ce a fost explicat anterior în segmentul similarității triunghiurilor. Apropo, liniile paralele pot fi, de asemenea, verticale sau paralele cu hipotenuza și se obțin triunghiuri similare în același mod.
A doua teoremă a lui Thales
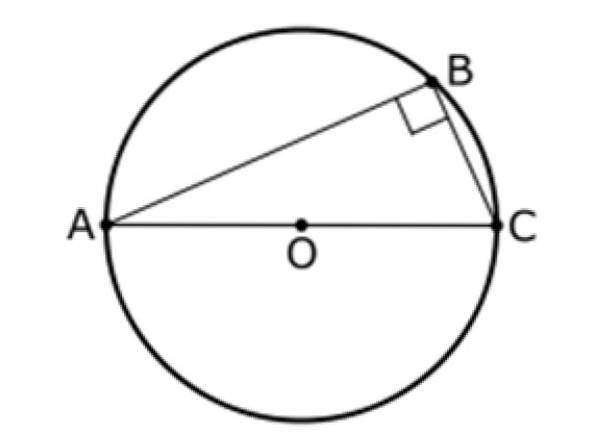
Această teoremă se referă, de asemenea, la un triunghi și un cerc cu centrul O, precum cele prezentate mai jos. În această figură, AC este un diametru al circumferinței și B este un punct, B fiind diferit de A și B.
A doua teoremă a lui Thales afirmă că:
Unghiul dintre segmentele AB și BC este întotdeauna de 90 °, prin urmare triunghiul ABC este drept.
Teorema lui Pitagora
Aceasta este una dintre cele mai faimoase teoreme din istorie. Se datorează matematicianului grec Pitagora din Samos (569 - 475 î.Hr.) și se aplică unui triunghi dreptunghiular. Spune așa:
Suma pătratelor lungimilor picioarelor triunghiului dreptunghiular este egală cu lungimea hipotenuzei pătrate.
Dacă luăm ca exemplu triunghiul albastru din figura 8 sau triunghiul violet, deoarece ambele sunt dreptunghiuri, atunci se poate afirma că:
ACDouă = ABDouă + Î.Hr.Două (triunghi albastru)
AC 'Două = AB 'Două + BC 'Două (triunghi violet)
Aria unui triunghi
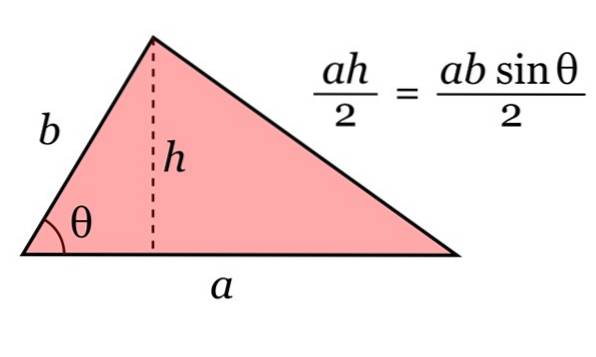
Aria triunghiului este dată de produsul bazei sale la și înălțimea ta h, împărțit la 2. Și la trigonometrie, această înălțime poate fi scrisă ca h = b sinθ.
Exemple de triunghiuri
Exemplul 1
Se spune că, prin intermediul primei sale teoreme, Thales a reușit să măsoare înălțimea Marii Piramide din Egipt, una dintre cele 7 minuni ale lumii antice, măsurând umbra pe care a proiectat-o pe sol și pe cea proiectată de un miză. condus în pământ..
Aceasta este schema procedurii urmată de Tales:
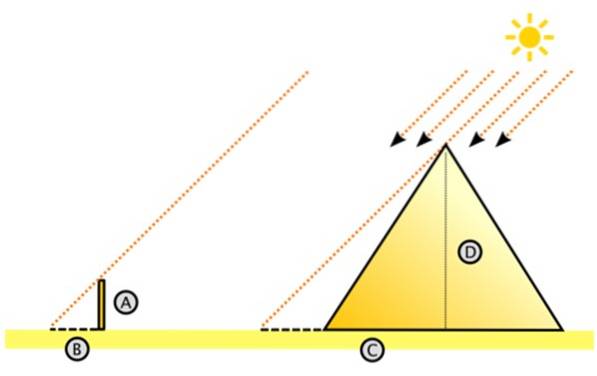
Thales a presupus corect că razele soarelui lovesc în paralel. Având în vedere acest lucru, și-a imaginat marele triunghi dreptunghiular din dreapta.
Acolo D este înălțimea piramidei și C este distanța deasupra solului măsurată de la centru până la umbra aruncată de piramidă pe podeaua deșertului. Poate fi laborios să măsoară C, dar este cu siguranță mai ușor decât măsurarea înălțimii piramidei.
În stânga se află triunghiul mic, cu picioarele A și B, unde A este înălțimea stâlpului condus vertical în pământ și B este umbra pe care o aruncă. Ambele lungimi sunt măsurabile, la fel și C (C este egal cu lungimea umbrei + jumătate din lungimea piramidei).
Deci, prin asemănarea triunghiurilor:
A / B = D / C
Și înălțimea Marii Piramide se dovedește a fi: D = C. (A / B)
Exemplul 2
Structurile din construcția civilă sunt structuri realizate din bare subțiri drepte, încrucișate, din lemn sau metal, care sunt folosite ca suport în multe clădiri. Sunt, de asemenea, cunoscute sub numele de zăbrele, grinzi sau zăbrele (fermă in engleza).
În ele triunghiurile sunt întotdeauna prezente, deoarece barele sunt interconectate în puncte numite noduri, care pot fi fixe sau articulate..

Exemplul 3
Metoda cunoscută sub numele de triangulație permite obținerea locației punctelor inaccesibile cunoscând alte distanțe care sunt mai ușor de măsurat, cu condiția să se formeze un triunghi care să includă locația dorită între vârfurile sale..
De exemplu, în figura următoare vrem să știm unde se află nava în mare, denumită B.
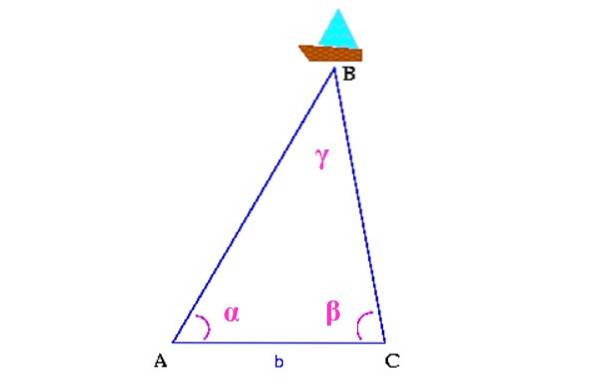
În primul rând, se măsoară distanța dintre două puncte de pe coastă, care în figură sunt A și C. Apoi, trebuie determinate unghiurile α și β, cu ajutorul unui teodolit, un dispozitiv folosit pentru măsurarea unghiurilor verticale și orizontale.
Cu toate aceste informații, este construit un triunghi în al cărui vârf superior este nava. Ar rămâne să calculăm unghiul γ, folosind proprietățile triunghiurilor și distanțele AB și CB folosind trigonometria, pentru a determina poziția navei în mare.
Instruire
Exercitiul 1
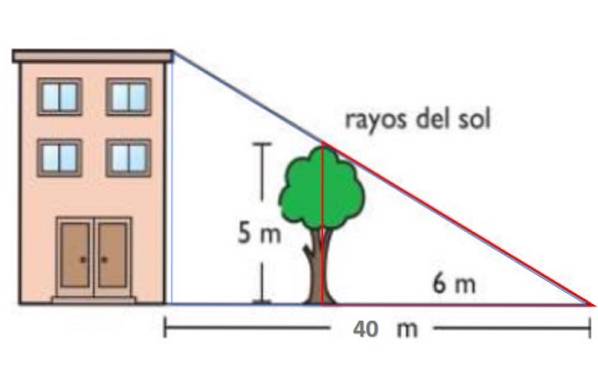
În figura prezentată, razele soarelui sunt paralele. În acest fel, arborele înalt de 5 metri aruncă o umbră de 6 metri pe sol. În același timp, umbra clădirii este de 40 de metri. Urmând Prima Teoremă a lui Thales, găsiți înălțimea clădirii.
Soluţie
Triunghiul roșu are laturi de 5 și respectiv 6 metri, în timp ce cel albastru are înălțimea H - înălțimea clădirii - și baza de 40 de metri. Ambele triunghiuri sunt similare, prin urmare:
H / 40 = 5/6 → H = 40. (5/6) m = 33,3 m
Exercițiul 2
Trebuie să cunoașteți distanța orizontală dintre două puncte LA Da B, dar sunt situate pe un teren foarte denivelat.
Despre punctul mediu (Pm) din acest teren se remarcă o proeminență de 1,75 metri înălțime. Dacă măsurarea benzii indică 26 de metri lungime măsurată de la A la proeminență și 27 de metri de la B la același punct, găsiți distanța AB.
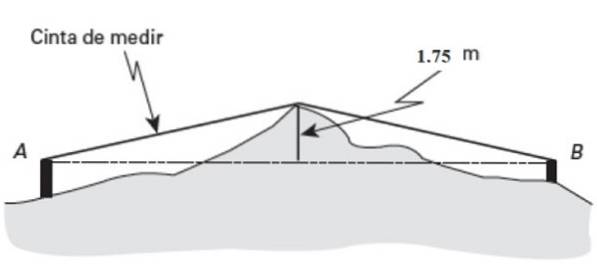
Soluţie
Teorema lui Pitagora se aplică unuia dintre cele două triunghiuri dreptunghiulare din figură. Începând cu cel din stânga:
Hipotenuză = c = 26 metri
Înălțime = a = 1,75 metri
APm = (26Două - 1,75Două)1/2 = 25,94 m
Acum aplicați Pitagora în triunghiul din dreapta, de data aceasta c = 27 metri, a = 1,75 metri. Cu aceste valori:
BPm= (27Două - 1,75Două)1/2 = 26,94 m
Distanța AB se găsește prin adăugarea acestor rezultate:
AB = 25,94 m + 26,94 m = 52,88 m.
Referințe
- Baldor, J. A. 1973. Geometria planului și spațiului. Cultural Central American.
- Barredo, D. Geometria triunghiului. Recuperat de pe: ficus.pntic.mec.es.
- Jiménez, R. 2010. Matematică II. Geometrie și trigonometrie. A doua editie. Pearson.
- Wentworth, G. Plane Geometry. Recuperat de pe: gutenberg.org.
- Wikipedia. Triunghi. Recuperat din: es. wikipedia.org.


Nimeni nu a comentat acest articol încă.