
Ecuația directoare vectorială a liniei, exerciții rezolvate
Se înțelege prin vector director una care definește direcția unei linii, fie în plan, fie în spațiu. Prin urmare, un vector paralel cu linia poate fi considerat ca un vector director al aceleiași.
Acest lucru este posibil datorită unei axiome a geometriei euclidiene care spune că două puncte definesc o linie. Apoi, segmentul orientat format din aceste două puncte definește și un vector director al liniei respective.
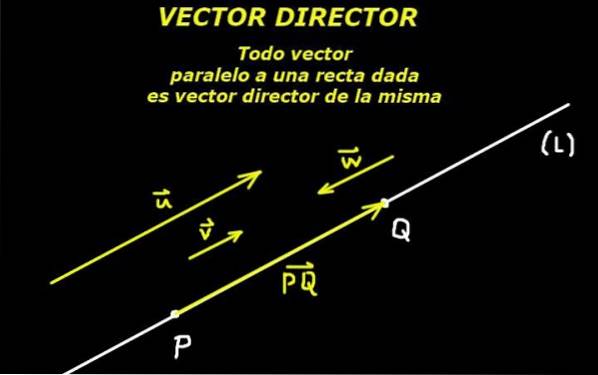
Având în vedere un punct P aparținând liniei (L) și a dat un vector director sau din acea linie, linia este complet determinată.
Indice articol
- 1 Ecuația vectorului de linie și director
- 1.1 Ecuația parametrică a liniei
- 2 Linia în formă vectorială
- 2.1 Exemplul 2
- 2.2 Forma continuă a liniei și a vectorului director
- 3 Forma generală a ecuației liniei
- 3.1 Exemplul 3
- 4 Forma standard a ecuației liniei
- 4.1 Exemplul 4
- 5 Exerciții rezolvate
- 5.1-Exercițiu 1
- 5.2 -Exerciția 2
- 6 Referințe
Ecuația liniei și a vectorului director
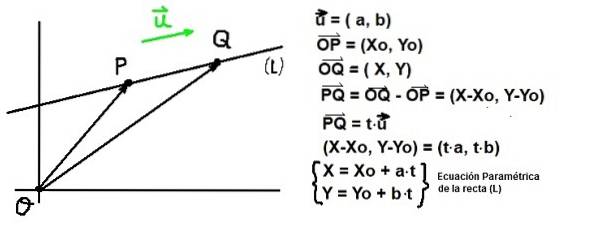
Având în vedere un punct P de coordonate Î: (Xo, I) și un vector sau director al unei drepte (L), toate punctele Î de coordonate Î: (X, Y) trebuie să satisfacă faptul că vectorul PQ fii paralel cu u. Această ultimă condiție este garantată dacă PQ este proporțional cu sau:
PQ = t⋅sau
în expresia anterioară t este un parametru care aparține numerelor reale.
Dacă componentele carteziene ale PQ și de sau Ecuația de mai sus este scrisă după cum urmează:
(X-Xo, Y-Yo) = t⋅ (a, b)
Dacă componentele egalității vectoriale sunt egalizate, avem următoarea pereche de ecuații:
X - Xo = a⋅t Da Y - I = b⋅t
Ecuația parametrică a liniei
Coordonatele X și Da a unui punct de pe linie (L) trecând printr-un punct de coordonate (Xo, I) și este paralel cu vector director sau= (a, b) sunt determinate prin atribuirea de valori reale parametrului variabil t:
X = Xo + a⋅t; Y = I + b⋅t
Exemplul 1
Pentru a ilustra semnificația ecuației parametrice a liniei, luăm ca vector de direcție
sau = (a, b) = (2, -1)
și ca punct cunoscut al liniei punctul
P = (Xo, I) = (1, 5).
Ecuația parametrică a liniei este:
X = 1 + 2⋅t; Y = 5 - 1⋅t; -∞
Pentru a ilustra semnificația acestei ecuații, este prezentată figura 3, unde parametrul t se schimbă în valoare și punct Î de coordonate (X Y) ia poziții diferite pe dreapta.
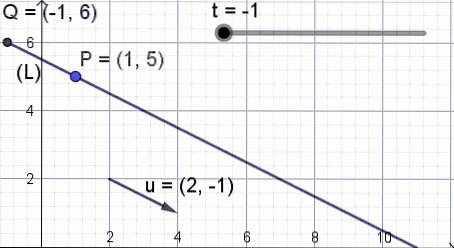
Linia în formă vectorială
Având în vedere un punct P pe linie și vectorul său director u, ecuația liniei poate fi scrisă în formă vectorială:
OQ = OP + λ⋅sau
În ecuația de mai sus Q este orice punct, dar aparține liniei și λ un număr real.
Ecuația vectorială a liniei este aplicabilă oricărui număr de dimensiuni, chiar și o hiperlinie poate fi definită.
În cazul tridimensional pentru un vector director sau= (a, b, c) și un punct P = (Xo, Yo, Zo), coordonatele unui punct generic Q = (X, Y, Z) aparținând liniei este:
(X ȘI Z) = (Xo, Yo, Zo) + λ⋅ (a, b, c)
Exemplul 2
Luați în considerare din nou linia care are drept vector de direcție
sau = (a, b) = (2, -1)
iar ca punct cunoscut al liniei punctul
P = (Xo, I) = (1, 5).
Ecuația vectorială a acestei linii este:
(X, Y) = (1, 5) + λ⋅ (2, -1)
Formă continuă a liniei și a vectorului director
Pornind de la forma parametrică, compensând și echivalând parametrul λ, avem:
(X-Xo) / a = (Y-Yo) / b = (Z-Zo) / c
Aceasta este forma simetrică a ecuației liniei. Simt că la, b Da c sunt componentele vectorului director.
Exemplul 3
Luați în considerare linia care are drept vector de direcție
sau = (a, b) = (2, -1)
iar ca punct cunoscut al liniei punctul
P = (Xo, I) = (1, 5). Găsiți forma sa simetrică.
Forma simetrică sau continuă a liniei este:
(X - 1) / 2 = (Y - 5) / (- 1)
Forma generală a ecuației liniei
Ecuația care are următoarea structură este cunoscută ca forma generală a liniei în planul XY:
A⋅X + B⋅Y = C
Expresia formei simetrice poate fi rescrisă pentru a avea forma generală:
b⋅X - a⋅Y = b⋅Xo - a⋅Yo
în comparație cu forma generală a liniei este:
A = b, B = -a și C = b⋅Xo - a⋅Yo
Exemplul 3
Găsiți forma generală a liniei al cărei vector director este u = (2, -1)
și care trece prin punctul P = (1, 5).
Pentru a găsi forma generală putem folosi formulele date, totuși se va alege o cale alternativă.
Începem prin a găsi vectorul dual w al vectorului director u, definit ca vectorul obținut prin schimbul componentelor lui u și înmulțirea celui de-al doilea cu -1:
w= (-1, -2)
vectorul dual w corespunde unei rotații de 90 ° în sensul acelor de ceasornic al vectorului director v.
Ne înmulțim scalar w cu (X Y) si cu (Xo, I) și ne potrivim:
(-1, -2) • (X, Y) = (-1, -2) • (1, 5)
-X-2Y = -1 -2⋅5 = -11
rămânând în cele din urmă:
X + 2Y = 11
Forma standard a ecuației liniei
Este cunoscută ca forma standard a liniei în planul XY, una care are următoarea structură:
Y = m⋅X + d
unde m reprezintă panta și d interceptarea cu axa Y.
Având în vedere vectorul de direcție u = (a, b), panta m este b / a.
Yd se obține prin înlocuirea punctului cunoscut Xo, Y pentru Xo, I:
I = (b / a) Xo + d.
Pe scurt, m = b / a și d = I - (b / a) Xo
Rețineți că panta m este coeficientul dintre componentă Da a vectorului director și a componentei X de acelasi.
Exemplul 4
Găsiți forma standard a liniei al cărei vector director este u = (2, -1)
și care trece prin punctul P = (1, 5).
m = -½ și d = 5 - (-½) 1 = 11/2
Y = (-1/2) X + 11/2
Exerciții rezolvate
-Exercitiul 1
Găsiți un vector director al liniei (L) care este intersecția planului (Π): X - Y + Z = 3 și planul (Ω): 2X + Y = 1.
Apoi scrieți forma continuă a ecuației liniei (L).
Soluţie
Din ecuația planului (Ω) clearance-ul Y: Y = 1 -2X
Apoi substituim în ecuația planului (Π):
X - (1 - 2X) + Z = 3 ⇒ 3X + Z = 4 ⇒ Z = 4 - 3X
Apoi parametrizăm X, alegem parametrizarea X = λ
Aceasta înseamnă că linia are o ecuație vectorială dată de:
(X, Y, Z) = (λ, 1 - 2λ, 4 - 3λ)
care poate fi rescris ca:
(X, Y, Z) = (0, 1, 4) + λ (1, -2, -3)
cu care este clar că vectorul sau = (1, -2, -3) este un vector director al liniei (L).
Forma continuă a liniei (L) este:
(X - 0) / 1 = (Y - 1) / (- 2) = (Z - 4) / (- 3)
-Exercițiul 2
Având în vedere planul 5X + la Y + 4Z = 5
și linia a cărei ecuație este X / 1 = (Y-2) / 3 = (Z -2) / (- 2)
Determinați valoarea la astfel încât planul și linia să fie paralele.
Soluția 2
Vectorul n = (5, a, 4) este un vector normal pentru plan.
Vectorul sau = (1, 3, -2) este un vector director al liniei.
Dacă linia este paralelă cu planul, atunci n • v = 0.
(5, la, 4)•(1, 3, -2) = 5 +3la -8 = 0 ⇒ la= 1.
Referințe
- Fleming, W. și Varberg, D. E. (1989). Precalcul Matematică. Prentice Hall PTR.
- Kolman, B. (2006). Algebră liniară. Pearson Education.
- Leal, J. M. și Viloria, N. G. (2005). Geometrie analitică plană. Mérida - Venezuela: Editorial Venezolana C. A.
- Navarro, Rocio. Vectori. Recuperat de la: books.google.co.ve.
- Pérez, C. D. (2006). Precalcul. Pearson Education.
- Prenowitz, W. 2012. Conceptele de bază ale geometriei. Rowman și Littlefield.
- Sullivan, M. (1997). Precalcul. Pearson Education.


Nimeni nu a comentat acest articol încă.