
Caracteristici, exemple și exerciții ale vectorilor concurenți
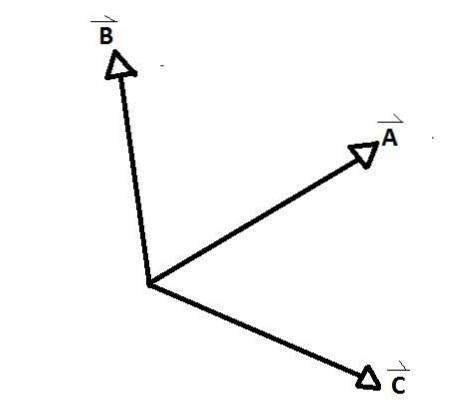
vectori concurenti sunt grupurile de vectori ale căror axe coincid într-un punct, formând între fiecare pereche a acestora un unghi intern și unul extern. Un exemplu clar este văzut în figura de mai jos, unde A, B și C sunt vectori concurenți între ei.
D și E spre deosebire de restul nu sunt. Există unghiuri formate între vectorii concurenți AB, AC și CB. Se numesc unghiuri de relație între vectori.
Indice articol
- 1 Caracteristici
- 2 Tipuri de vectori
- 3 Notare vectorială
- 3.1 cartezian
- 3.2 Polar
- 3.3 Analitic
- 3.4 Sferic
- 4 Operații cu vectori concurenți
- 4.1 Suma (A + B)
- 4.2 Diferență (A - B)
- 4.3 Produs scalar (A. B)
- 4.4 Produs vector (A x B)
- 5 Exemple: exerciții rezolvate
- 5.1 Exercițiul 1
- 5.2 Exercițiul 2
- 6 Exerciții propuse
- 7 Referințe
Caracteristici
-Au un punct comun, care coincide cu originea lor: toate mărimile vectorilor concurenți pleacă de la un punct comun la extremele lor respective..
-Originea este considerată punctul de acțiune al vectorului: trebuie stabilit un punct de acțiune care va fi direct afectat de fiecare dintre vectorii concurenți.
-Domeniul său în plan și spațiu este RDouă și R3 respectiv: vectorii concurenți sunt liberi să acopere întregul spațiu geometric.
-Permite notații diferite în același grup de vectori. Conform ramurilor de studiu, diferite notații sunt prezente în operațiile cu vectori.
Tipuri de vectori
Ramura vectorilor are mai multe subdiviziuni, dintre care unele pot fi denumite: paralel, perpendicular, coplanar, corespunzător, opus și unitar. Vectorii concurenți sunt enumerați aici și, ca toți cei menționați mai sus, au multe aplicații în diferite științe..
Sunt foarte frecvente în studiul vectorilor, deoarece reprezintă o generalizare utilă în operațiile cu aceștia. Atât în plan, cât și în spațiu, vectorii concurenți sunt utilizați în mod obișnuit pentru a reprezenta diferite elemente și a studia influența lor asupra unui anumit sistem..
Notare vectorială
Există mai multe moduri de a reprezenta un element vector. Principalele și cele mai cunoscute sunt:
Cartezian
Propus de aceeași abordare matematică, denotă vectorii cu un triplu corespunzător mărimilor fiecărei axe (x, y, z)
A: (1, 1, -1) Spațiul A: (1, 1) Avion
Polar
Ele servesc doar la desemnarea vectorilor din plan, deși în calculul integral li se atribuie componenta de adâncime. Este compus cu o magnitudine liniară r și un unghi față de axa polară Ɵ.
A: (3, 450 ) Planul A: (2, 450 , 3) Spațiu
Analitic
Ele definesc mărimile vectorului folosind versorii. Versorii (i + j + k) reprezintă vectorii unitari corespunzători axelor X Y Da
A: 3i + 2j - 3k
Sferic
Acestea sunt similare cu notația polară, dar cu adăugarea unui al doilea unghi care străbate planul X y simbolizat prin δ.
A: (4, 60sau , π / 4)
Operații vectoriale concurente
Vectorii concurenți sunt utilizați în cea mai mare parte pentru a defini operațiuni între vectori, deoarece este mai ușor să comparați elementele vectorilor atunci când sunt prezentate simultan..
Suma (A + B)
Suma vectorilor concurenți are ca scop găsirea vectorului rezultat Vr. Care, conform ramurii de studiu, corespunde unei acțiuni finale
De exemplu: 3 șiruri A, B, C sunt legate de o cutie, fiecare capăt al șirului este ținut de un subiect. Fiecare dintre cei 3 subiecți trebuie să tragă frânghia într-o direcție diferită de celelalte 2.
A: (ax, ay, az) B: (bx, by, bz) C: (cx, cy, cz)
A + B + C = (ax + bx + cx; ay + by + cy; az + bz + cz) = Vr
Prin urmare, caseta se va putea deplasa într-o singură direcție Vr va indica direcția și direcția de mișcare a cutiei.
Diferență (A - B)
Există multe criterii în ceea ce privește diferența dintre vectori, mulți autori aleg să o excludă și afirmă că este stipulată doar suma dintre vectori, unde diferența este de aproximativ suma vectorului opus. Adevărul este că algebric vectorii pot fi scăși.
A: (ax, ay, az) B: (bx, by, bz)
A - B = A + (-B) = (ax-bx; ay-by; az-bz) = [ax + (-bx); ay + (-by); az + (-bz)]
Produs scalar (A. B)
De asemenea, cunoscut sub numele de produs dot, generează o valoare scalară care poate fi legată de diferite magnitudini în funcție de ramura de studiu..
Pentru geometrie indică aria paralelogramului format de perechea de vectori concurenți prin metoda paralelogramului. Căci fizica mecanică definește munca realizată de o forță F la deplasarea unui corp la distanță Δr.
ѡ = F . Δr
După cum indică și numele, generează o valoare scalară și este definită după cum urmează:
Să fie vectorii A și B
A: (ax, ay, az) B: (bx, by, bz)
-Forma analitică:
(A. B) = | A |. | B | .Cos θ
Unde θ este unghiul intern dintre ambii vectori
-Forma algebrică:
(A. B) = (ax.bx + ay.by + az.bz)
Produs încrucișat (A x B)
Produsul încrucișat sau produs punctual între doi vectori, definește un al treilea vector C care are calitatea de a fi perpendicular pe B Da C. În fizică definiți vectorul cuplului τ element de bază al dinamicii de rotație.
-Forma analitică:
| A x B | = | A |. | B | .Sen θ
-Forma algebrică:
(A x B) = = (Ax. By - ay. Bx) - (ax. Bz - az. Bx) j + (ax. by - ay. bx) k
-Mișcare relativă: rA / B
Baza relativității este mișcarea relativă, iar vectorii concurenți sunt baza mișcării relative. Pozițiile relative, vitezele și accelerațiile pot fi deduse aplicând următoarea ordine de idei.
r A / B = rLA - rB ; Poziția relativă a lui A față de B
v A / B = vLA - vB ; Viteza relativă a lui A față de B
la A / B = aLA - laB ; Accelerația relativă a lui A față de B
Exemple: exerciții rezolvate
Exercitiul 1
Fie A, B și C vectori simultan.
A = (-1, 3, 5) B = (3, 5, -2) C = (-4, -2, 1)
-Definiți vectorul rezultat Vr = 2A - 3B + C
2A = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)
-3B = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)
Vr = 2A + (-3B) + C = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)
Vr = ([-2 + (- 9) + (- 4)]; [6 + (- 15) + (- 2)]; (10 + 6 + 1))
Vr = (-15, -11, 17)
-Definiți produsul punct (A. C)
(A. C) = (-1, 3, 5). (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4 - 6 + 5
(A. C) = 3
-Calculați unghiul dintre A și C
(A. C) = | A |. | C |. Cos θ Unde θ este unghiul cel mai scurt dintre vectori
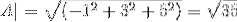
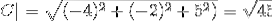
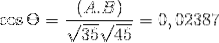
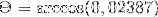
θ = 88,630
-Găsiți un vector perpendicular pe A și B
Pentru aceasta este necesar să se definească produsul vector între (-1, 3, 5) și (3, 5, -2). Așa cum s-a explicat mai înainte, se construiește o matrice 3 x 3 unde primul rând este compus din vectorii de unități triple (i, j, k). Apoi, al doilea și al treilea rând sunt alcătuite din vectorii de operat, respectând ordinea operațională.
(A x B) = = [(-1). 5 - (3. 3)] eu - [(-1). (-2) - (5. 3)] j + [(-1). 5 - (3. 3)] k
(A x B) = (-5 - 9) Eu - (2 - 15) j + (-5 - 9) k
(A x B) = -14 I + 13 j - 14 k
Exercițiul 2
Să Vla și Vb vectorii vitezei lui A și respectiv B. Calculați viteza lui B văzută din A.
Vla = (3, -1, 5) Vb = (2, 5, -3)
În acest caz, se solicită viteza relativă a lui B față de A VB / A
VB / A = VB - VLA
VB / A = (2, 5, -3) - (3, -1, 5) = (-1, 6, -8)
Acesta este vectorul vitezei lui B văzut din A. În cazul în care este descris un nou vector al vitezei lui B, luând referință de la un observator poziționat la A și care se mișcă cu viteza lui A.
Exerciții propuse
1-Construiește 3 vectori A, B și C care sunt concurenți și raportează 3 operații între ei printr-un exercițiu practic.
2-Fie vectorii A: (-2, 4, -11), B: (1, -6, 9) și C: (-2, -1, 10). Găsiți vectori perpendiculari pe: A și B, C și B, suma A + B + C.
4-Determinați 3 vectori care sunt perpendiculari unul pe celălalt, fără a lua în considerare axele de coordonate.
5-Definiți munca efectuată de o forță care ridică un bloc de masă de 5 kg, de la fundul unui puț de 20m adâncime.
6-Arătați algebric că scăderea vectorilor este egală cu suma vectorului opus. Justificați-vă postulatele.
7-Denotați un vector în toate notațiile dezvoltate în acest articol. (Cartezian, polar, analitic și sferic).
8-Forțele magnetice exercitate asupra unui magnet care se sprijină pe o masă, sunt date de următorii vectori; V: (5, 3, -2), T: (4, 7, 9), H: (-3, 5, -4). Determinați în ce direcție se va mișca magnetul dacă toate forțele magnetice acționează în același timp.
Referințe
- Geometrie și transformări euclidiene. Clayton W. Dodge. Courier Corporation, 1 ianuarie 2004
- Cum se rezolvă probleme de matematică aplicată L. Moiseiwitsch. Courier Corporation, 10 aprilie 2013
- Concepte de bază ale geometriei. Walter Prenowitz, Meyer Jordan. Rowman & Littlefield, 4 oct 2012
- Vectori. Rocío Navarro Lacoba, 7 iunie. 2014
- Algebră liniară. Bernard Kolman, David R. Hill. Pearson Education, 2006



Nimeni nu a comentat acest articol încă.