
Definirea vitezei unghiulare, formula, calculul și exercițiile
viteză unghiulară este o măsură a vitezei de rotație și este definită ca unghiul pe care vectorul de poziție al obiectului rotativ îl rotește, pe unitate de timp. Este o magnitudine care descrie foarte bine mișcarea unei multitudini de obiecte care se rotesc constant peste tot: CD-uri, roți de mașini, mașini, Pământ și multe altele..
O diagramă a „ochiului londonez” poate fi văzută în figura următoare. Reprezintă mișcarea unui pasager reprezentat de punctul P, care urmează calea circulară, numită c:
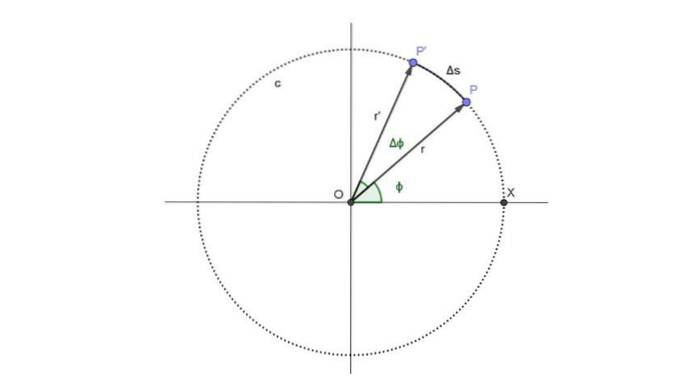
Pasagerul ocupă poziția P la momentul t și poziția unghiulară corespunzătoare acelui moment este ϕ.
Din momentul t, se scurge o perioadă de timp Δt. În această perioadă, noua poziție a pasagerului punctual este P ', iar poziția unghiulară a crescut cu un unghi Δϕ.
Indice articol
- 1 Cum calculați viteza unghiulară ?
- 1.1 Relația dintre viteza liniară și unghiulară
- 2 Mișcare de rotație uniformă
- 3 S-au rezolvat probleme de viteză unghiulară
- 3.1 Exercițiul 1
- 4 Exercițiul 2
- 4.1 Exercițiul 3
- 4.2 Exercițiul 4
- 5 Referințe
Cum calculați viteza unghiulară ?
Pentru cantitățile de rotație, literele grecești sunt utilizate pe scară largă pentru a le diferenția de cantitățile liniare. Deci inițial definim viteza unghiulară medie ωm ca unghiul parcurs într-o anumită perioadă de timp.
Atunci coeficientul Δϕ / Δt va reprezenta viteza unghiulară medie ωm între timpurile t și t + Δt.
Dacă doriți să calculați viteză unghiulară tocmai în momentul t, atunci va trebui să calculăm coeficientul Δϕ / Δt când Δt ➡0:

Relația dintre viteza liniară și unghiulară
Viteza liniară v, este coeficientul dintre distanța parcursă și timpul necesar parcurgerii acesteia.
În figura de mai sus, arcul parcurs este Δs. Dar acel arc este proporțional cu unghiul parcurs și raza, relația următoare fiind îndeplinită, care este valabilă atâta timp cât Δϕ este măsurat în radiani:
Δs = r ・ Δϕ
Dacă împărțim expresia anterioară la intervalul de timp Δt și luăm limita când Δt ➡0, vom obține:
v = r ・ ω
Mișcare de rotație uniformă

O mișcare de rotație este uniformă dacă, în orice moment observat, unghiul parcurs este același în aceeași perioadă de timp.
Dacă rotația este uniformă, atunci viteza unghiulară în orice moment coincide cu viteza unghiulară medie.

Mai mult, atunci când se face o întoarcere completă, unghiul parcurs este de 2π (echivalent cu 360 °). Prin urmare, într-o rotație uniformă, viteza unghiulară ω este legată de perioada T, prin următoarea formulă:

f = 1 / T
Cu alte cuvinte, într-o rotație uniformă, viteza unghiulară este legată de frecvență prin:
ω = 2π ・ f
S-au rezolvat probleme de viteză unghiulară
Exercitiul 1
Cabinele marii roți rotative cunoscute sub numele de „London Eye”Se mișcă încet. Viteza cabinei este de 26 cm / s, iar roata are un diametru de 135 m.
Cu aceste date calculați:
i) Viteza unghiulară a roții
ii) Frecvența de rotație
iii) Timpul necesar unei cabine pentru a face un viraj complet.
Răspunsuri:
i) Viteza v în m / s este: v = 26 cm / s = 0,26 m / s.
Raza este jumătate din diametru: r = (135 m) / 2 = 67,5 m
v = r ・ ω => ω = v / r = (0,26 m / s) / (67,5 m) = 0,00385 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (0,00385 rad / s) / (2π rad) = 6,13 x 10-4 ture / s
f = 6,13 x 10 ^ -4 tura / s = 0,0368 tura / min = 2,21 tura / oră.
iii) T = 1 / f = 1 / 2,21 tur / oră = 0,45311 oră = 27 min 11 sec
Exercițiul 2
O mașină de jucărie se deplasează pe o pistă circulară cu o rază de 2m. La 0 s poziția sa unghiulară este 0 rad, dar după un timp t poziția sa unghiulară este dată de:
φ (t) = 2 ・ t
A determina:
i) Viteza unghiulară
ii) Viteza liniară în orice moment.
Răspunsuri:
i) Viteza unghiulară este derivata poziției unghiulare: ω = φ '(t) = 2.
Adică mașina de jucărie are în orice moment o viteză unghiulară constantă egală cu 2 rad / s.
ii) Viteza liniară a mașinii este: v = r ・ ω = 2 m ・ 2 rad / s = 4 m / s = 14,4 Km / h
Exercițiul 3
Aceeași mașină din exercițiul anterior începe să se oprească. Poziția sa unghiulară în funcție de timp este dată de următoarea expresie:
φ (t) = 2 ・ t - 0,5 ・ tDouă
A determina:
i) Viteza unghiulară în orice moment
ii) Viteza liniară în orice moment
iii) Timpul necesar pentru a se opri din momentul în care începe să încetinească
iv) Unghiul parcurs
v) distanța parcursă
Răspunsuri:
i) Viteza unghiulară este derivata poziției unghiulare: ω = φ '(t)
ω (t) = φ '(t) = (2 ・ t - 0,5 ・ tDouă) '= 2 - t
ii) Viteza liniară a mașinii în orice moment este dată de:
v (t) = r ・ ω (t) = 2 ・ (2 - t) = 4 - 2 t
iii) Timpul necesar pentru a se opri din momentul în care începe să decelereze, este determinat de cunoașterea momentului în care viteza v (t) devine zero.
v (t) = 4 - 2 t = 0 => t = 2
Adică se oprește 2 s după ce începe să frâneze.
iv) În perioada de 2s de când începe să frâneze până când se oprește, se parcurge un unghi dat de φ (2):
φ (2) = 2 ・ 2 - 0,5 ・ 2 ^ 2 = 4 - 2 = 2 rad = 2 x 180 / π = 114,6 grade
v) În perioada de 2 s de când începe să frâneze până când se oprește, o distanță s dată de:
s = r ・ φ = 2m ・ 2 rad = 4 m
Exercițiul 4
Roțile unei mașini au un diametru de 80 cm. Dacă mașina circulă cu 100 km / h. Găsiți: i) viteza unghiulară de rotație a roților, ii) frecvența de rotație a roților, iii) numărul de rotații pe care roata le face într-o călătorie de 1 oră.
Răspunsuri:
i) Mai întâi vom converti viteza mașinii de la Km / h la m / s
v = 100 Km / h = (100 / 3,6) m / s = 27,78 m / s
Viteza unghiulară de rotație a roților este dată de:
ω = v / r = (27,78 m / s) / (0,4 m) = 69,44 rad / s
ii) Frecvența de rotație a roților este dată de:
f = ω / 2π = (69,44 rad / s) / (2π rad) = 11,05 tura / s
Frecvența de rotație este de obicei exprimată în rotații pe minut r.p.m.
f = 11,05 tura / s = 11,05 tura / (1/60) min = 663,15 r.p.m
iii) Numărul de ture efectuate de roată într-o călătorie de 1 oră se calculează știind că 1 oră = 60 min și că frecvența este numărul de ture N împărțit la timpul în care se efectuează acele N ture.
f = N / t => N = f ・ t = 663,15 (ture / min) x 60 min = 39788,7 ture.
Referințe
- Giancoli, D. Fizică. Principii cu aplicații. Ediția a 6-a. Prentice Hall. 106-108.
- Resnick, R. (1999). Fizic. Volumul 1. Ediția a treia în limba spaniolă. Mexic. Compañía Editorial Continental S.A. de C.V. 67-69.
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7. Ediție. Mexic. Editorii de învățare Cengage. 84-85.
- geogebra.org



Nimeni nu a comentat acest articol încă.