platformă factorială Este o mașină simplă care constă dintr-un aranjament de scripete cu efect multiplicator al forței. În acest fel, o sarcină poate fi ridicată aplicând doar echivalentul unei fracțiuni din greutate la capătul liber al frânghiei..
Se compune din două seturi de scripeți: unul care este fixat pe un suport și altul care exercită forța rezultată asupra sarcinii. Scripetele sunt montate pe un cadru general metalic care le ține.
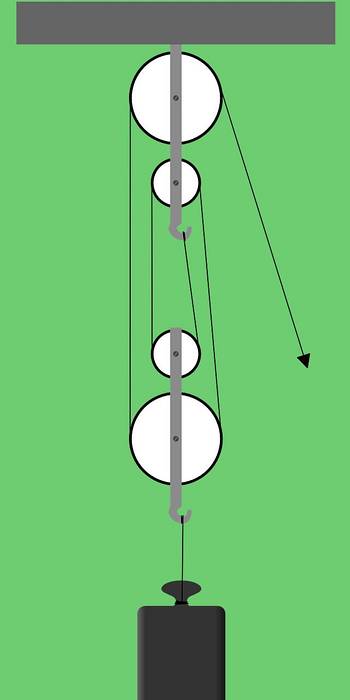
Figura 1 prezintă o platformă factorială formată din două grupuri de câte două scripeți. Acest tip de aranjament de scripete se mai numește montaj serial sau palanuri.
Indice articol
Pentru a înțelege de ce această dispunere înmulțește forța exercitată, vom începe cu cel mai simplu caz, care constă dintr-un scripete fix și un scripete mobil..
În figura 2 avem un scripete A fixat de tavan cu ajutorul unui suport. Rola A se poate roti liber în jurul axei sale. Avem, de asemenea, un scripete B care are un suport atașat la arborele fuliei, pe care este așezată sarcina. Rola B, pe lângă faptul că poate roti liber în jurul axei sale, are posibilitatea de a se deplasa vertical.
Să presupunem că suntem într-o situație de echilibru. Luați în considerare forțele care acționează asupra scripetului B. Axa scripetelui B suportă o greutate totală P care este îndreptată în jos. Dacă aceasta ar fi singura forță pe scripetele B, atunci ar cădea, dar știm că frânghia care trece prin acest scripete exercită și două forțe, care sunt T1 și T2 care sunt direcționate în sus..
Pentru a exista un echilibru translațional, cele două forțe ascendente trebuie să fie egale cu greutatea susținută de axa fuliei B.
T1 + T2 = P
Dar, deoarece scripetele B se află și în echilibru de rotație, atunci T1 = T2. Forțele T1 și T2 provin din tensiunea aplicată șirului, numită T.
Prin urmare T1 = T2 = T. Înlocuind în ecuația anterioară rămâne:
T + T = P
2T = P
Ceea ce indică faptul că tensiunea aplicată coardei este doar jumătate din greutate:
T = P / 2
De exemplu, dacă sarcina ar fi de 100 kg, ar fi suficient să se aplice o forță de 50 kg la capătul liber al frânghiei pentru a ridica sarcina la o viteză constantă..
Să luăm acum în considerare tensiunile și forțele care acționează asupra unui ansamblu format din două aranjamente ale suporturilor A și B cu câte două scripeți..
Suportul B are posibilitatea de a se deplasa vertical, iar forțele care acționează asupra acestuia sunt:
- Greutatea P a sarcinii, îndreptată vertical în jos.
- Două solicitări pe scripetele mari și două solicitări pe scripetele mici. În total, patru tensiuni, toate orientate în sus.
Pentru a exista un echilibru translațional este necesar ca forțele îndreptate vertical în sus să fie egale în valoare cu sarcina îndreptată în jos. Adică trebuie îndeplinit:
T + T + T + T = P
Adică 4 T = P
Din care rezultă că forța aplicată T la capătul liber al frânghiei este doar un sfert din greutate datorită sarcinii care se dorește a fi ridicată., T = P / 4.
Cu această valoare pentru tensiunea T, sarcina poate fi menținută statică sau poate crește cu viteză constantă. Dacă s-ar aplica o tensiune mai mare decât această valoare, atunci sarcina ar accelera în sus, o condiție care este necesară pentru ao scoate din repaus..
Conform celor observate în cazurile anterioare, pentru fiecare scripete a ansamblului mobil există câteva forțe ascendente exercitate de frânghia care trece prin scripete. Dar această forță nu poate fi altceva decât tensiunea aplicată coardei la capătul liber.
Astfel încât pentru fiecare scripete a ansamblului mobil să existe o forță verticală ascendentă egală cu 2T. Dar, deoarece există n scripete în ansamblul mobil, rezultă că forța totală îndreptată vertical în sus este:
2 n T
Pentru a exista un echilibru vertical este necesar ca:
2 n T = P
prin urmare, forța aplicată la capătul liber este:
T = P / (2 n)
În acest caz se poate spune că forța exercitată T se înmulțește de 2 ori pe sarcină.
De exemplu, dacă am avea o platformă factorială cu 3 scripeți fixi și 3 scripeți mobili, numărul n ar fi egal cu 3. Pe de altă parte, dacă sarcina ar fi P = 120 kg, atunci forța aplicată la capătul liber ar fi T = 120 kg / (2 * 3) = 20 kg.
Luați în considerare o platformă factorială formată din două scripete fixe și două scripete mobile. Tensiunea maximă pe care o poate rezista coarda este de 60 kg. Determinați care este sarcina maximă care poate fi plasată.
Când sarcina este în repaus sau în mișcare cu viteză constantă, greutatea sa P este legată de tensiunea T aplicată cablului prin următoarea relație:
P = 2 n T
Deoarece este un aparat cu două scripeți mobili și două scripeți fixi, atunci n = 2.
Sarcina maximă care poate fi plasată se obține atunci când T are valoarea maximă posibilă, care în acest caz este de 60 kg.
Sarcina maximă = 2 * 2 * 60kg = 240kg
Găsiți relația dintre tensiunea cablului și greutatea sarcinii, într-o platformă factorială cu două scripete în care sarcina este accelerată cu accelerație la.
Diferența acestui exemplu față de ceea ce sa văzut până acum este că dinamica sistemului trebuie luată în considerare. Deci, propunem a doua lege a lui Newton pentru a găsi relația solicitată.
În figura 4 desenăm în galben forțele datorate tensiunii T a frânghiei. Partea în mișcare a palanului are o masă totală M. Luăm ca sistem de referință unul la nivelul primei scripete fixe și pozitiv în jos.
Y1 este cea mai joasă poziție a arborelui fuliei.
Aplicăm a doua lege a lui Newton pentru a determina accelerația a1 a părții mobile a platformei:
-4 T + Mg = M a1
Deoarece greutatea sarcinii este P = Mg, unde g este accelerația gravitației, relația de mai sus poate fi scrisă:
-4T + P = P (a1 / g)
Dacă am dori să determinăm tensiunea aplicată cablului atunci când o anumită sarcină P este accelerată cu accelerația a1, atunci relația anterioară ar arăta astfel:
T = P (1 - a1 / g) / 4
Rețineți că dacă sistemul ar fi în repaus sau în mișcare cu viteză constantă, atunci a1 = 0 și am recupera aceeași expresie pe care am obținut-o în cazul 2.
În acest exemplu, se utilizează același accesoriu de la exercițiul 1, cu aceeași frânghie care suportă maximum 60 kg de tensiune. O anumită sarcină este ridicată, accelerând-o de la repaus la 1 m / s în 0,5 s, folosind tensiunea maximă a corzii. Găsiți greutatea maximă a sarcinii.
Vom folosi expresiile obținute în exercițiul 2 și sistemul de referință din figura 4 în care direcția pozitivă este verticală în jos.
Accelerația sarcinii este a1 = (-1 m / s - 0 m / s) / 0,5 s = -2 m / s ^ 2.
Greutatea sarcinii în kilograme-forță este dată de
P = 4 T / (1 - a1 / g)
P = 4 * 60 kg / (1 + 2 / 9,8) = 199,3 kg
Aceasta este greutatea maximă posibilă a sarcinii fără ruperea frânghiei. Rețineți că valoarea obținută este mai mică decât cea obținută în exemplul 1, în care sarcina a fost presupusă a avea o accelerație zero, adică în repaus sau cu viteză constantă..
Nimeni nu a comentat acest articol încă.