Șocuri elastice într-o singură dimensiune, cazuri speciale, exerciții

șocuri elastice sau coliziunile elastice constau în interacțiuni scurte, dar intense între obiecte, în care sunt conservate atât impulsul, cât și energia cinetică. Accidentele sunt evenimente foarte frecvente în natură: de la particule subatomice la galaxii, la bile de biliard și mașini de protecție în parcurile de distracții, toate acestea sunt obiecte capabile să se ciocnească.

În timpul unei coliziuni sau coliziuni, forțele de interacțiune dintre obiecte sunt foarte puternice, mult mai mult decât cele care pot acționa extern. În acest fel se poate afirma că în timpul coliziunii, particulele formează un sistem izolat.

În acest caz, este adevărat că:

P_sau = P_F

Cantitatea de mișcare P_sau înainte de coliziune este la fel ca după coliziune. Acest lucru este valabil pentru orice tip de coliziune, atât elastică, cât și inelastică..

Acum luați în considerare următoarele: în timpul unei coliziuni obiectele suferă o anumită deformare. Când șocul este elastic, obiectele își recapătă rapid forma originală.

Indice articol

• 1 Conservarea energiei cinetice
• 2 Șocuri elastice într-o singură dimensiune
  • 2.1 -Formule pentru coliziuni elastice
• 3 Cazuri speciale în coliziuni elastice
  • 3.1 Două mase identice
  • 3.2 Două mase identice, dintre care una a fost inițial în repaus
  • 3.3 Două mase diferite, una dintre ele inițial în repaus
• 4 Coeficientul de restituire sau regula Huygens-Newton
• 5 Exerciții rezolvate
  • 5.1 - Exercițiu rezolvat 1
  • 5.2 - Exercițiu rezolvat 2
  • 5.3 - Exercițiu rezolvat 3
  • 5.4 - Exercițiu rezolvat 4
• 6 Referințe

Conservarea energiei cinetice

În mod normal în timpul unui accident, o parte din energia obiectelor este cheltuită pe căldură, deformare, sunet și uneori chiar pe producerea de lumină. Deci, energia cinetică a sistemului după coliziune este mai mică decât energia cinetică originală.

Când energia cinetică K este conservată atunci:

K_sau = K_F

Ceea ce înseamnă că forțele care acționează în timpul coliziunii sunt conservatoare. În timpul coliziunii, energia cinetică este transformată pe scurt în energie potențială și apoi înapoi la energia cinetică. Energiile cinetice respective variază, dar suma rămâne constantă.

Coliziunile perfect elastice sunt rare, deși bilele de biliard sunt o aproximare destul de bună, la fel ca și coliziile care apar între moleculele de gaz ideale..

Șocuri elastice într-o singură dimensiune

Să examinăm o coliziune a două particule din aceasta într-o singură dimensiune; adică particulele care interacționează se mișcă, să zicem, de-a lungul axei x. Să presupunem că au mase m₁ Da m_Două. Viteza inițială a fiecăruia este sau₁ Da sau_Două respectiv. Vitezele finale sunt v₁ Da v_Două.

Putem renunța la notația vectorială, deoarece mișcarea se efectuează de-a lungul axei x, însă semnele (-) și (+) indică direcția mișcării. În stânga este negativ și în dreapta pozitiv, prin convenție.

-Formule pentru coliziuni elastice

Pentru cantitatea de mișcare

m₁sau₁ + m_Douăsau_Două = m₁v₁ + m_Douăv_Două

Pentru energia cinetică

½ m₁sau^Două₁ + ½ m_Douăsau^Două_Două = ½ m₁v^Două₁ +  ½ m_Douăv^Două_Două

Cu condiția să se cunoască masele și viteza inițială, ecuațiile pot fi regrupate pentru a găsi viteza finală.

Problema este că, în principiu, este necesar să se realizeze o algebră puțin plictisitoare, deoarece ecuațiile pentru energia cinetică conțin pătratele vitezei, ceea ce face calculul un pic greoi. Idealul ar fi să găsim expresii care nu le conțin.

Primul lucru este de a face fără factorul ½ și de a rearanja ambele ecuații în așa fel încât să apară un semn negativ și masele să poată fi luate în considerare:

m₁sau₁ - m₁v₁ = M_Douăv_Două - m_Douăsau_Două

m₁sau^Două₁ - m₁v^Două₁  = + M_Douăv^Două_Două - m_Douăsau^Două_Două

Fiind exprimat în acest fel:

m₁(sau₁ - v₁ ) = m_Două(v_Două - sau_Două)

m₁(sau^Două₁ - v^Două₁ ) = m_Două (v^Două_Două - sau^Două_Două)

Simplificare pentru a elimina pătratele vitezei

Acum trebuie să folosim produsul suma notabilă prin diferența sa în a doua ecuație, cu care obținem o expresie care nu conține pătratele, așa cum se dorea inițial:

m₁(sau₁ - v₁ ) = m_Două(v_Două - sau_Două)

m₁(sau₁ - v₁ ) (sau₁ + v₁ ) = m_Două (v_Două - sau_Două) (v_Două + sau_Două)

Următorul pas este înlocuirea primei ecuații din a doua:

m_Două(v_Două - sau_Două) (sau₁ + v₁ ) = m_Două (v_Două - sau_Două) (v_Două + sau_Două)

Și când termenul se repetă m_Două(v_Două - sau_Două) de ambele părți ale egalității, termenul menționat este anulat și arată astfel:

(sau₁ + v₁) = (v_Două + sau_Două)

Sau chiar mai bine:

sau₁ - sau_Două= v_Două -  v₁

Viteze finale v₁ și V_Două a particulelor

Acum aveți două ecuații liniare cu care sunt mai ușor de lucrat. Le vom pune înapoi una sub alta:

m₁sau₁ + m_Douăsau_Două = m₁v₁ + m_Douăv_Două

sau₁ - sau_Două= v_Două -  v₁

Înmulțind a doua ecuație cu m₁ și adăugarea termenului la termen este:

m₁sau₁ + m_Douăsau_Două = m₁v₁ + m_Douăv_Două

m₁sau₁ - m₁sau_Două= m₁v_Două - m₁ v₁

-

2 m₁sau₁ + (m_Două - m₁) sau_Două = (m_Două + m₁) v_Două

Și este deja posibil să clarificăm v_Două. De exemplu:

Cazuri speciale în coliziuni elastice

Acum că sunt disponibile ecuații pentru viteza finală a ambelor particule, este timpul să analizăm câteva situații speciale.

Două mase identice

Atunci m₁ = m_Două = m Y:

v₁ = u_Două

v_Două = u₁

Particulele își schimbă pur și simplu viteza după coliziune.

Două mase identice, dintre care una a fost inițial în repaus

Din nou  m₁ = m_Două = m și presupunând că sau₁ = 0:

v₁ = u_Două

v_Două = 0

După coliziune, particula aflată în repaus capătă aceeași viteză cu particula care se mișca, iar aceasta la rândul ei se oprește.

Două mase diferite, una dintre ele inițial în repaus

În acest caz, să presupunem că sau₁ = 0, dar masele sunt diferite:

Ce-ar fi dacă m₁ este mult mai mare decât m_Două?

Se întâmplă ca m₁ este încă în repaus și m_Două revine la fel de repede ca a lovit.

Coeficientul de restituire sau regula Huygens-Newton

Anterior, următoarea relație între viteze a fost derivată pentru două obiecte aflate în coliziune elastică: sau₁ - sau_Două = v_Două -  v₁. Aceste diferențe sunt viteza relativă înainte și după coliziune. În general, pentru o coliziune este adevărat că:

sau₁ - sau_Două = - (v₁ -  v_Două)

Conceptul de viteză relativă este cel mai bine apreciat dacă cititorul își imaginează că se află pe una dintre particule și din această poziție observă viteza cu care se deplasează cealaltă particulă. Ecuația de mai sus este rescrisă astfel:

Exerciții rezolvate

-Exercițiu rezolvat 1

O bilă de biliard se deplasează spre stânga la 30 cm / s, ciocnind frontal cu o altă bilă identică care se deplasează spre dreapta la 20 cm / s. Cele două bile au aceeași masă, iar coliziunea este perfect elastică. Găsirea vitezei fiecărei mingi după impact.

Soluţie

sau₁ = -30 cm / s

sau_Două = +20 cm / s

Este cazul special în care două mase identice se ciocnesc elastic într-o singură dimensiune, prin urmare se schimbă vitezele.

v₁ = +20 cm / s

v_Două = -30 cm / s

-Exercițiu rezolvat 2

Coeficientul de restituire a unei mingi care sări de pe sol este egal cu 0,82. Dacă cade din repaus, ce fracțiune din înălțimea sa inițială va atinge mingea după ce va sări o dată? Și după 3 sări?

Soluţie

Solul poate fi obiectul 1 în ecuația coeficientului de restituire. Și rămâne întotdeauna odihnit, astfel încât:

Cu această viteză, ricoșează:

Semnul + indică faptul că este o viteză ascendentă. Și conform acestuia, mingea atinge o înălțime maximă de:

Acum revine din nou la pământ cu o viteză de aceeași magnitudine, dar semnul opus:

Aceasta atinge o înălțime maximă de:

Reveniți la pământ cu:

Salturi succesive

De fiecare dată când mingea sare și crește, înmulțiți din nou viteza cu 0,82:

Până acum h₃ este de aproximativ 30% din h_sau. Care ar fi înălțimea până la al 6-lea săritură fără a fi nevoie să faceți calcule atât de detaliate precum cele precedente?

Ar fi h₆ = 0,82¹² h_sau = 0,092h_sau sau doar 9% din h_sau.

-Exercițiu rezolvat 3

Un bloc de 300 g se deplasează spre nord la 50 cm / s și se ciocnește cu un bloc de 200 g care se îndreaptă spre sud, la 100 cm / s. Să presupunem că șocul este perfect elastic. Găsiți viteza după impact.

Date

m₁ = 300 g; sau₁ = + 50 cm / s

m_Două = 200 g; sau_Două = -100 cm / s

-Exercițiu rezolvat 4

Se eliberează o masă de m₁ = 4 kg de la punctul indicat pe pista fără frecare, până când se ciocnește cu m_Două = 10 kg în repaus. Cât de mare crește m?₁ după coliziune?

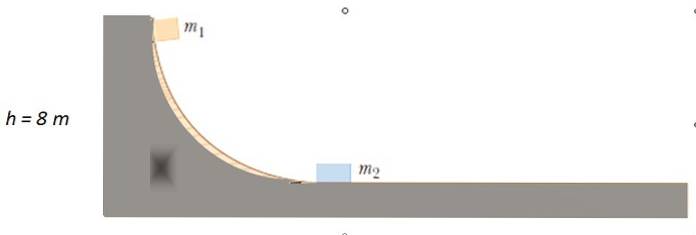
Soluţie

Deoarece nu există frecare, energia mecanică este conservată pentru a găsi viteza sau₁ cu ce m₁ impacturi  m_Două. Inițial energia cinetică este 0, deoarece m₁ o parte din odihnă. Când se deplasează pe suprafața orizontală nu are înălțime, deci energia potențială este 0.

mgh = ½ mu₁ ^Două

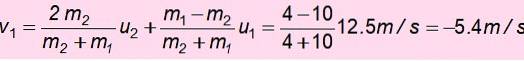
sau_Două = 0

Acum viteza de m₁ după coliziune:

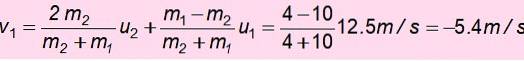
Semnul negativ înseamnă că a fost returnat. Cu această viteză crește și energia mecanică este conservată din nou pentru a o găsi h ', înălțimea la care puteți urca după prăbușire:

½ mv₁^Două = mgh '

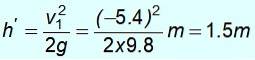
Rețineți că nu revine la punctul de plecare la o altitudine de 8 m. Nu are suficientă energie, deoarece masa a dat o parte din energia sa cinetică m_1.

Referințe

1. Giancoli, D. 2006. Fizică: principii cu aplicații. 6^a. Sala Ed Prentice. 175-181
2. Rex, A. 2011. Fundamentele fizicii. Pearson. 135-155.
3. Serway, R., Vulle, C. 2011. Fundamentele fizicii. 9^{n / A} Cengage Learning. 172-182
4. Tipler, P. (2006) Fizică pentru știință și tehnologie. Ediția a 5-a Volumul 1. Editorial Reverté. 217-238
5. Tippens, P. 2011. Fizică: concepte și aplicații. Ediția a VII-a. MacGraw Hill. 185-195