
Elemente cvadrilaterale, proprietăți, clasificare, exemple
A patrulater este un poligon cu patru laturi și patru vârfuri. Al lor părți opuse sunt cele care nu au vârfuri în comun, în timp ce sunt laturi consecutive cei cu un vârf comun.
Într-un patrulater sunt unghiuri adiacente cei care împărtășesc o parte, în timp ce unghiuri opuse nu au părți comune. O altă caracteristică importantă a unui patrulater este că suma celor patru unghiuri interne este de două ori unghiul plan, adică 360º sau 2π radiani.
Diagonale sunt segmentele care unesc un vârf cu opusul său și într-un patrulater dat, din fiecare vârf poate fi trasă o singură diagonală. Numărul total de diagonale într-un patrulater este de două.
Cadrilaterele sunt figuri cunoscute omenirii din cele mai vechi timpuri. Înregistrările arheologice, precum și construcțiile care supraviețuiesc astăzi, atestă acest lucru..
La fel, astăzi patrulaterele continuă să aibă o prezență importantă în viața de zi cu zi a tuturor. Cititorul poate găsi acest formular pe ecranul în care textul este citit chiar în acest moment, pe ferestre, uși, piese auto și nenumărate alte locuri..
Indice articol
- 1 Clasificarea patrulaterelor
- 1.1 Tipuri de paralelogram
- 2 Trapez
- 2.1 Tipuri de trapezoide
- 3 Paralelogramă
- 3.1 Aria unui paralelogram
- 3.2 Diagonalele unui paralelogram
- 3.3 Legea paralelogramelor
- 4 Dreptunghi
- 4.1 Diagonalele unui dreptunghi
- 5 Pătrat
- 6 Romb
- 7 Exemple
- 7.1 Exemplul 1
- 7.2 Exemplul 2
- 7.3 Exemplul 3
- 8 Exerciții rezolvate
- 8.1 - Exercițiul 1
- 8.2 - Exercițiul 2
- 9 Referințe
Clasificare cvadrilaterală
Conform paralelismului laturilor opuse, patrulaterele sunt clasificate după cum urmează:
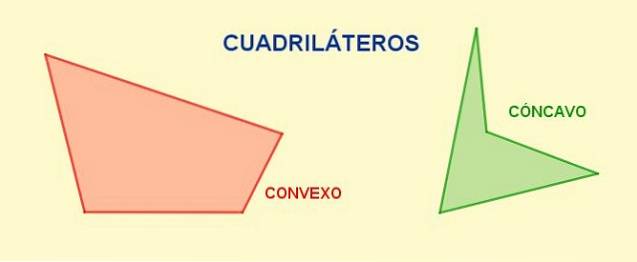
- Trapez, când nu există paralelism și patrulaterul este convex.
- Trapez, când există paralelism între o singură pereche de laturi opuse.
- Paralelogram, când laturile sale opuse sunt paralele două câte două.
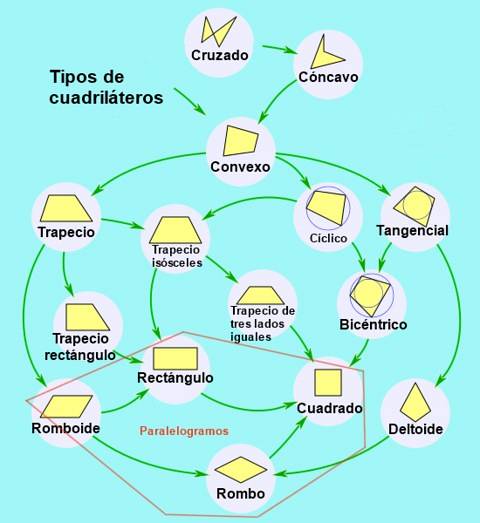
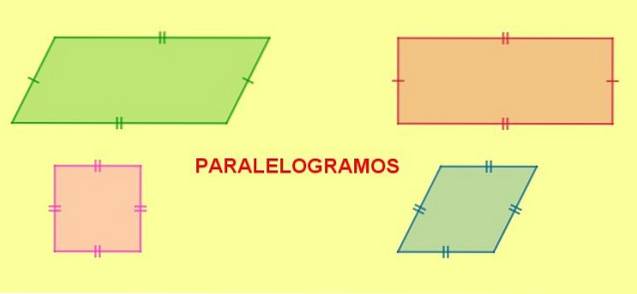
Tipuri de paralelogram
La rândul lor, paralelogramele pot fi clasificate în funcție de unghiurile și laturile lor după cum urmează:
- Dreptunghi, este paralelogramul care are cele patru unghiuri interne de măsură egală. Unghiurile interioare ale unui dreptunghi formează un unghi drept (90º).
- Pătrat, este un dreptunghi cu cele patru laturi de aceeași măsură.
- Diamant, este paralelogramul cu cele patru laturi egale ale acestuia, dar unghiuri adiacente diferite.
- Romboid, paralelogram cu diferite unghiuri adiacente.
Trapez
Trapezul este un patrulater convex cu două laturi paralele.
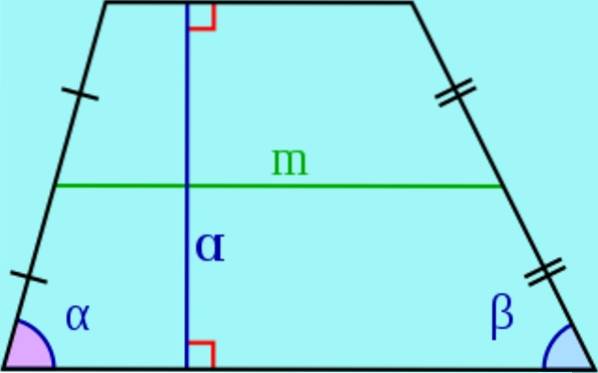
- Într-un trapez se numesc laturile paralele baze iar nonparalelele sunt numite lateral.
- înălţime a unui trapez este distanța dintre cele două baze, adică lungimea unui segment cu capete la baze și perpendiculare pe ele. Acest segment este numit și înălțimea trapezului..
- median este segmentul care unește punctele medii ale lateralelor. Se poate arăta că mediana este paralelă cu bazele trapezului și lungimea acestuia este egală cu semisuma bazelor.
- Aria unui trapez este înălțimea sa înmulțită cu semi-suma bazelor:
Aria unui trapez = înălțime * (baza 1 + baza 2) / 2
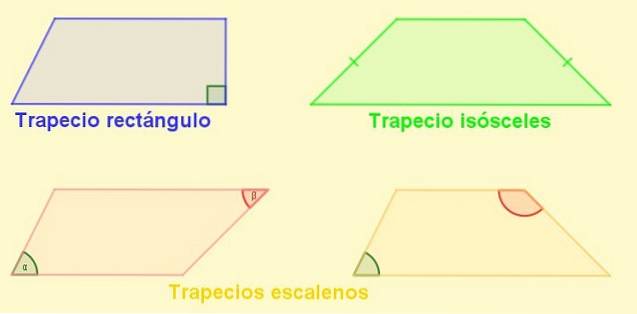
Tipuri de trapezoide
-Trapez dreptunghiular: Este cel cu o perpendiculară laterală pe baze. Acest lateral este, de asemenea, înălțimea trapezului.
-Izoscel trapez: Cel cu laturile de lungime egală. Într-un trapez isoscel unghiurile adiacente bazelor sunt egale.
-Trapezoid scalen: Cel cu laturile sale de diferite lungimi. Unghiurile sale opuse pot fi una acută și cealaltă obtuză, dar se poate întâmpla și ca ambele să fie obtuse sau ambele să fie acute..
Paralelogram
Paralelogramul este un patrulater ale cărui laturi opuse sunt paralele două câte două. Într-un paralelogram unghiurile opuse sunt egale, iar unghiurile adiacente sunt suplimentare sau, cu alte cuvinte, unghiurile adiacente se adaugă la 180º.
Dacă un paralelogram are un unghi drept, atunci toate celelalte unghiuri vor fi și ele, iar figura rezultată se numește dreptunghi. Dar dacă dreptunghiul are și laturile sale adiacente de aceeași lungime, atunci toate laturile sale sunt egale și figura rezultată este a pătrat.
Când un paralelogram are două laturi adiacente de aceeași lungime, toate laturile sale vor avea aceeași lungime și figura rezultată este a diamant.
Înălțimea unui paralelogram este un segment cu capete pe laturile sale opuse și perpendiculare pe ele..
Zona unui paralelogram
Zona unui paralelogram este produsul bazei de înălțimea sa, baza fiind o latură perpendiculară pe înălțime (figura 6).
Aria unui paralelogram = baza x înălțimea = a. h
Diagonalele unui paralelogram
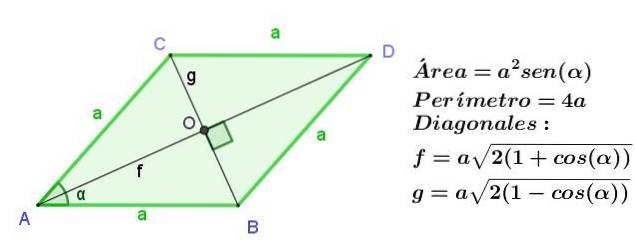
Pătratul diagonalei care începe de la un vârf este egal cu suma pătratelor celor două laturi adiacente vârfului menționat plus produsul dublu al acestor laturi de cosinusul unghiului acelui vârf:
FDouă = aDouă + dDouă + 2 a d Cos (α)
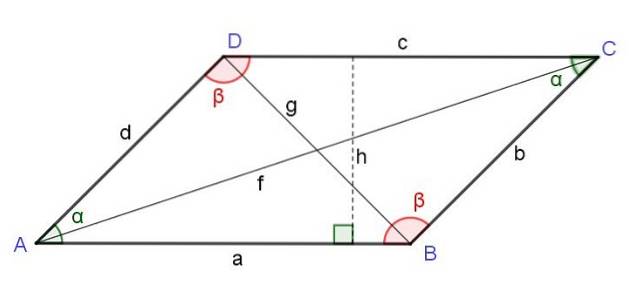
Pătratul diagonalei opuse vârfului unui paralelogram este egal cu suma pătratelor celor două laturi adiacente vârfului menționat și scăderea produsului dublu al acestor laturi de cosinusul unghiului acelui vârf:
gDouă = aDouă + dDouă - 2 a d Cos (α)
Legea paralelogramelor
În orice paralelogram suma pătratelor laturilor sale este egală cu suma pătratelor diagonalelor:
laDouă + bDouă + cDouă + dDouă = fDouă + gDouă
Rectangle
Dreptunghiul este un patrulater cu laturile sale opuse paralele două câte două și care are și un unghi drept. Cu alte cuvinte, dreptunghiul este un tip de paralelogram cu unghi drept. Pentru că este paralelogram, dreptunghiul are laturi opuse de lungime egală a = c și b = d.
Dar, ca în orice paralelogram, unghiurile adiacente sunt suplimentare și unghiurile opuse egale, în dreptunghi, deoarece are un unghi drept, va forma în mod necesar unghiuri drepte în celelalte trei unghiuri. Și anume într-un dreptunghi toate unghiurile interioare măsoară 90º sau π / 2 radiani.
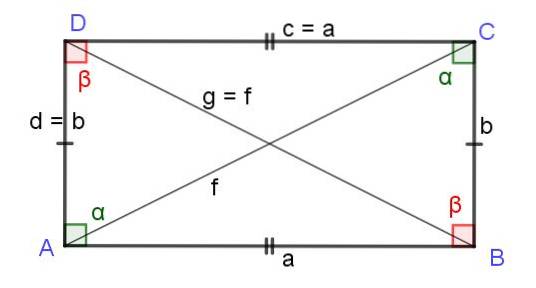
Diagonalele unui dreptunghi
Într-un dreptunghi diagonalele sunt de lungime egală, așa cum se va demonstra mai jos. Raționamentul este următorul; Un dreptunghi este un paralelogram cu toate unghiurile sale drepte și, prin urmare, moștenește toate proprietățile paralelogramului, inclusiv formula care dă lungimea diagonalelor:
FDouă = aDouă+ dDouă + 2 a d Cos (α)
gDouă = aDouă + dDouă - 2 a d Cos (α)
cu α = 90º
Ce Cos (90º) = 0, atunci se întâmplă că:
FDouă = gDouă = aDouă + dDouă
Acesta este f = g, și deci lungimile F Da g dintre cele două diagonale ale dreptunghiului sunt egale și lungimea lor este dată de:
Lungimea diagonalelor unui dreptunghi = √ (aDouă + bDouă)
De asemenea, dacă este într-un dreptunghi cu laturile adiacente la Da b o parte este luată ca bază, cealaltă parte va fi înălțime și, prin urmare, aria dreptunghiului va fi:
Aria dreptunghiului = a x b.
Perimetrul este suma tuturor laturilor dreptunghiului, dar din moment ce contrariile sunt egale, rezultă că pentru un dreptunghi cu laturi la Da b perimetrul este dat de următoarea formulă:
Perimetrul dreptunghiului = 2 (a + b)
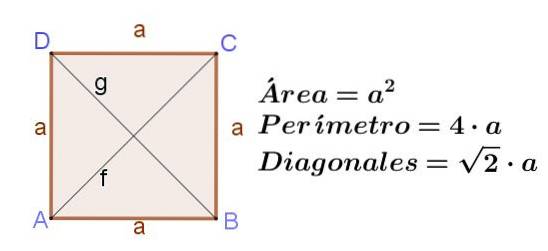
Pătrat
Pătratul este un dreptunghi cu laturile sale adiacente de aceeași lungime. Dacă pătratul are o latură la, apoi diagonalele sale F Da g au aceeași lungime, adică f = g = (√2) a.
Suprafața unui pătrat este partea pătrată:
Suprafața unui pătrat = aDouă
Perimetrul unui pătrat este de două ori latura:
Perimetrul unui pătrat = 4 a
Diamant
Rombul este un paralelogram cu laturile sale adiacente de aceeași lungime, dar ca într-un paralelogram laturile opuse sunt egale atunci, toate laturile unui romb au o lungime egală.
Diagonalele unui romb sunt de lungime diferită, dar se intersectează în unghi drept.
Exemple
Exemplul 1
Arătați că într-un patrulater (neîncrucișat) unghiurile interne se ridică la 360 °.
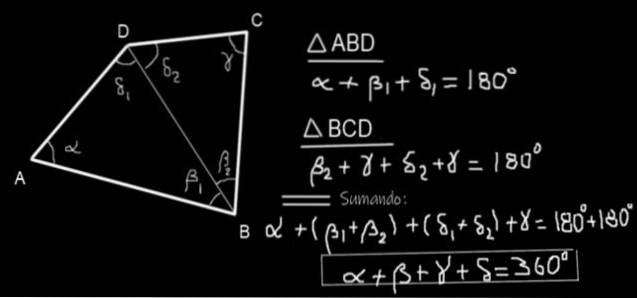
Se ia în considerare un patrulater ABCD (vezi figura 10) și se trasează diagonala BD. Se formează două triunghiuri ABD și BCD. Suma unghiurilor interioare ale triunghiului ABD este:
α + β1 + δ1 = 180º
Iar suma unghiurilor interne ale triunghiului BCD este:
β2 + γ + δDouă = 180º
Adunând cele două ecuații obținem:
α + β1 + δ1 + βDouă + γ + δDouă = 180º + 180º
Gruparea:
α + (β1 + βDouă) + (δ1 + δDouă) + γ = 2 * 180º
Prin grupare și redenumire, se arată în cele din urmă că:
α + β + δ + γ = 360º
Exemplul 2
Arătați că mediana unui trapez este paralelă cu bazele sale și lungimea sa este semisuma bazelor.
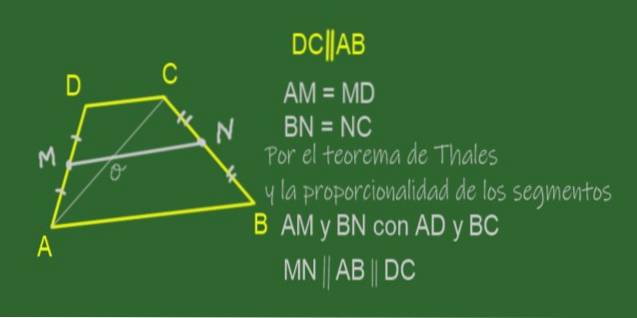
Mediana unui trapez este segmentul care unește punctele medii ale laturilor sale, adică laturile neparalele. În trapezul ABCD prezentat în figura 11 mediana este MN.
Deoarece M este punctul mediu al AD și N este punctul mediu al BC, este adevărat că raporturile AM / AD și BN / BC sunt egale.
Adică, AM este proporțional cu BN în aceeași proporție cu AD este față de BC, deci sunt date condițiile pentru aplicarea teoremei Thales (reciprocă) care afirmă următoarele:
"Dacă segmentele proporționale sunt determinate în trei sau mai multe linii tăiate de două secante, atunci aceste linii sunt toate paralele".
În cazul nostru, se concluzionează că liniile MN, AB și DC sunt paralele între ele, prin urmare:
„Lmediana unui trapez este paralelă cu bazele sale".
Acum se va aplica teorema Thales:
"Un set de paralele tăiate de două sau mai multe secante determină segmente proporționale".
În cazul nostru AD = 2 AM, AC = 2 AO, deci triunghiul DAC este similar cu triunghiul MAO și, în consecință, DC = 2 MO.
Un argument similar ne permite să afirmăm că CAB este similar cu CON, unde CA = 2 CO și CB = 2 CN. Urmează imediat că AB = 2 ON.
Pe scurt, AB = 2 ON și DC = 2 MO. Deci, atunci când adăugăm, avem:
AB + DC = 2 ON + 2 MO = 2 (MO + ON) = 2 MN
În cele din urmă, MN este șters:
MN = (AB + DC) / 2
Și se concluzionează că mediana unui trapez măsoară semi-suma bazelor, sau cu alte cuvinte: mediana măsoară suma bazelor, împărțită la două.
Exemplul 3
Arată că într-un romb diagonalele se intersectează în unghi drept.

Tabla din figura 12 prezintă construcția necesară. Mai întâi paralelogramul ABCD este desenat cu AB = BC, adică un romb. Diagonalele AC și DB determină opt unghiuri prezentate în figură.
Folosind teorema (a.i.p.) care afirmă că alternează unghiuri interioare între paralele tăiate printr-o secantă determină unghiuri egale, putem stabili următoarele:
α1 = γ1, α2 = γ2, δ1 = Β1 și δ2 = β2. (*)
Pe de altă parte, deoarece laturile adiacente ale unui romb sunt de lungime egală, se determină patru triunghiuri isoscele:
DAB, BCD, CDA și ABC
Acum se invocă teorema triunghiului (isoscel), care afirmă că unghiurile adiacente bazei sunt de măsură egală, din care se concluzionează că:
δ1 = β2, δ2 = β1, α2 = γ1 și α1 = γ2 (**)
Dacă relațiile (*) și (**) sunt combinate, se ajunge la următorul egal de unghi:
α1 = α2 = γ1 = γ1 pe de o parte și β1 = Β2 = δ1 = δ2 pe de altă parte.
Reamintind teorema triunghiurilor egale care afirmă că două triunghiuri cu o latură egală între două unghiuri egale sunt egale, avem:
AOD = AOB și, prin urmare, și unghiurile ∡AOD = ∡AOB.
Apoi ∡AOD + ∡AOB = 180º, dar din moment ce ambele unghiuri sunt de măsură egală, avem 2 ∡AOD = 180º ceea ce implică faptul că ∡AOD = 90º.
Adică, se arată geometric că diagonalele unui romb se intersectează în unghi drept.
Exerciții rezolvate
- Exercitiul 1
Arată că într-un trapez drept, unghiurile non-drepte sunt suplimentare.
Soluţie
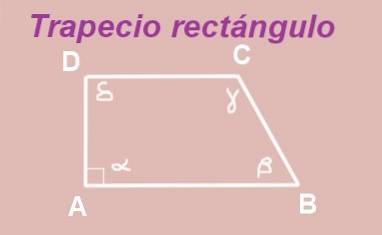
Trapezul ABCD este construit cu bazele AB și DC paralele. Unghiul interior al vârfului A este drept (măsoară 90º), deci avem un trapez drept.
Unghiurile α și δ sunt unghiuri interne între două paralele AB și DC, prin urmare sunt egale, adică δ = α = 90º.
Pe de altă parte, s-a arătat că suma unghiurilor interne ale unui patrulater se adaugă la 360 °, adică:
α + β + γ + δ = 90º + β + 90º + δ = 360º.
Cele de mai sus conduc la:
β + δ = 180º
Confirmând ceea ce se dorea să se arate, că unghiurile β și δ sunt suplimentare.
- Exercițiul 2
Un paralelogram ABCD are AB = 2 cm și AD = 1 cm, în plus unghiul BAD este de 30º. Determinați aria paralelogramului menționat și lungimea celor două diagonale ale acestuia.
Soluţie
Aria unui paralelogram este produsul lungimii bazei sale de înălțimea sa. În acest caz, lungimea segmentului b = AB = 2 cm va fi luată ca bază, cealaltă parte are lungimea a = AD = 1 cm și înălțimea h va fi calculată după cum urmează:
h = AD * Sen (30º) = 1 cm * (1/2) = ½ cm.
Deci: Suprafață = b * h = 2 cm * ½ cm = 1 cmDouă.
Referințe
- C. E. A. (2003). Elemente de geometrie: cu exerciții și geometria busolei. Universitatea din Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematică 2. Grupo Editorial Patria.
- Eliberat, K. (2007). Descoperiți poligoanele. Benchmark Education Company.
- Hendrik, V. (2013). Poligoane generalizate. Birkhäuser.
- IGER. (s.f.). Matematică Primul semestru Tacaná. IGER.
- Jr. geometrie. (2014). Poligoane. Lulu Press, Inc..
- Miller, Heeren și Hornsby. (2006). Matematică: raționament și aplicații (ediția a zecea). Pearson Education.
- Patiño, M. (2006). Matematică 5. Editorial Progreso.
- Wikipedia. Cadrilaterale. Recuperat de pe: es.wikipedia.com

Nimeni nu a comentat acest articol încă.