Corp rigid

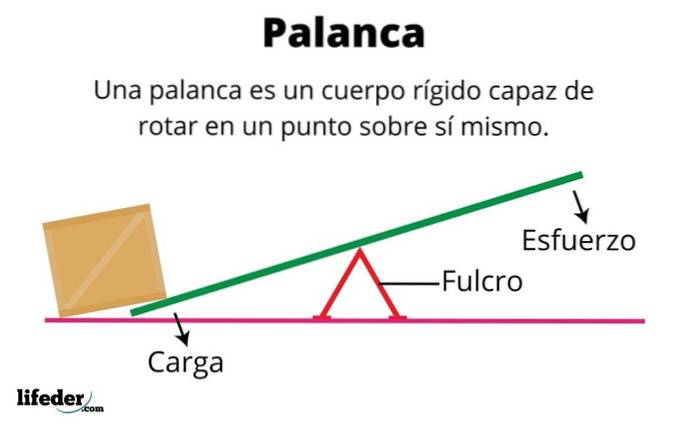
Ce este un corp rigid?

Un corp rigid este un obiect material ale cărui particule rămân întotdeauna în aceleași poziții relative. Prin urmare, este un obiect care nu se deformează, o calitate atribuită forțelor puternice de coeziune care țin particulele la locul lor..

În realitate, particulele oricărui corp supus forțelor externe tind să vibreze sau să se miște, astfel încât obiectul se deformează întotdeauna într-o oarecare măsură, dar aceste efecte sunt de obicei mici.

Când acesta este cazul, se poate presupune că corpul este rigid și are o foarte bună aproximare a comportamentului său, chiar dacă este o idealizare.

Tipuri de corpuri rigide

Se pot distinge două tipuri de corp rigid:

• Cei ale căror particule vin în cantități discrete, adică pot fi numărate. De exemplu, două sfere metalice unite printr-o tijă subțire și ușoară pot fi considerate ca o singură entitate. Dacă tija este suficient de rigidă pentru a nu se îndoaie, sistemul este considerat un corp rigid.
• Cele care sunt continue, ceea ce înseamnă că particulele care le compun nu pot fi distinse. Obiectele de zi cu zi și natura sunt exemple bune: pietre, mobilier și altele, precum și Pământul și alte corpuri cerești stâncoase.

Mișcarea și dinamica rigidă a corpului

La fel ca obiectele considerate particule, corpurile rigide se pot traduce, roti și au o mișcare mai generală, combinând translația și rotația.

Pentru a studia traducerea, nu este necesar să se analizeze separat mișcarea fiecărei particule, ci mai degrabă mișcarea centrului de masă, un punct în care se consideră că toată masa obiectului este concentrată..

Aceste mișcări de translație și rotație pot fi:

• Independent, ca și în cazul planetelor, care au o mișcare de rotație în jurul axei lor (considerate fixe) și o mișcare de translație în jurul Soarelui, dar viteza fiecărei nu este legată..
• Roto-traducere, dacă viteza unghiulară și viteza de translație a centrului de masă sunt corelate. În acest caz, axa de rotație este mobilă, ca în cazul cilindrului care se rostogolește pe o pantă abruptă fără a aluneca..

Dinamica corpului rigid

Următoarele cantități sunt relevante în dinamica corpului rigid:

Centrul de masă

Centrul de masă este punctul în care toată masa corpului este considerată concentrată. Dacă este un corp omogen și simetric, cum ar fi o sferă, centrul de masă coincide cu centrul geometric.

Moment de inerție

Această magnitudine scalară este valoarea inerției de rotație sau a rezistenței pe care un obiect se opune să o rotească în jurul unei anumite axe. Depinde în totalitate de geometria obiectului și de masa acestuia și, prin urmare, în anumite cazuri, este mai ușor să se rotească în jurul anumitor axe decât altele..

Pentru corpurile cu forme geometrice bine definite, există tabele cu momentele de inerție în raport cu axele de simetrie, de exemplu, cel care trece prin centrul de masă. Cu aceste informații și teoremele legate de momentul de inerție, momentele despre alte axe pot fi ușor calculate..

Forțe și cuplu sau cuplu

Este nevoie de forțe pentru a mișca un corp. Dacă centrul de masă al solidului rigid este tradus, ecuația mișcării, conform celei de-a doua legi a lui Newton, este:

F_net = M ∙la_cm

Unde:

-Forța netă este F_net

-M este masa

-Accelerarea centrului de masă este la_cm

Cu toate acestea, nu toate forțele aplicate reușesc să determine rotirea obiectului. Acest lucru necesită cuplul sau cuplul, care arată cât de eficientă este acțiunea de rotație a unei forțe. Este definit ca produsul vectorial între vectorul de poziție r în ceea ce privește un anumit punct O și forța F în cauză. Este notat prin litera greacă τ (cu caractere aldine, deoarece este și un vector):

τ = r × F

În sistemul internațional SI, unitatea pentru cuplu este N⋅m (newton pe metru).

În multe cazuri, mișcarea de rotație în jurul unei axe prin centrul de masă este descrisă printr-o ecuație analogă celei de-a doua legi a lui Newton:

Energia cinetică a unui solid rigid

Mișcarea unui corp rigid este descrisă prin traduceri ale centrului de masă și rotații în jurul acelui punct, prin urmare, energia sa cinetică are ambele contribuții.

Fie K energia cinetică a corpului, v_cm viteza centrului de masă, M masa corpului, I_cm momentul său de inerție cu privire la centrul de masă și ω viteza unghiulară. Se poate demonstra că energia cinetică este:

K = ½ Mv_cm^Două + ½ I_cm ω^Două

Se observă că al doilea termen din dreapta este analogul de rotație al termenului din stânga. Acolo momentul de inerție joacă același rol ca masa, în timp ce viteza unghiulară are același rol ca viteza liniară..

Exemple în viața de zi cu zi

Pendul fizic

Pendulul fizic sau pendulul real este foarte ușor de construit: constă dintr-un solid rigid, cum ar fi o tijă sau o bară, oscilând liber în jurul unei axe orizontale. Axa de rotație nu trece prin centrul de masă al obiectului și aceasta, în principiu, poate avea orice formă.

Acest pendul diferă de pendulul simplu, deoarece în acesta din urmă masa care o compune este considerată a fi punctuală.

Roată de bicicletă

Un alt exemplu de corp rigid cunoscut este roata bicicletei, a cărei axă trece prin centrul de masă, care trece prin centrul roții. Atâta timp cât nu se înclină spre o parte sau se rotește, ecuațiile dinamicii descrise mai sus se aplică pentru a descrie mișcarea acesteia..

O minge de bowling

Modelul solid rigid este potrivit pentru a descrie mișcarea mingii de bowling pe bandă sau atunci când rulează fără a aluneca pe rampa de întoarcere.

Yoyo

Această jucărie populară este realizată cu un cilindru din lemn sau plastic și un șnur înfășurat într-o canelură care o înconjoară..

Cilindrul poate fi modelat ca un corp rigid în care tensiunea din șir asigură cuplul pentru viraj, în timp ce greutatea (aplicată la centrul de masă) și tensiunea sunt responsabile pentru accelerația verticală a centrului de masă..

Referințe

1. Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill. 
2. Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
3.  Katz, D. 2013. Fizica pentru oamenii de știință și ingineri. Fundamente și conexiuni. Cengage Learning.
4. Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 1. Pearson.
5. Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7. Ed. Cengage Learning.