diferențele dintre viteză și viteză există, chiar dacă ambele sunt mărimi fizice înrudite. În limbajul comun, un termen sau altul este folosit în mod interschimbabil ca și cum ar fi sinonime, dar în Fizică este necesar să se facă distincția între ele..
Acest articol definește ambele concepte, subliniază diferențele și explică, folosind exemple, cum și când se aplică unul sau altul. Pentru a simplifica, luăm în considerare o particulă în mișcare și de aici vom revizui conceptele de viteză și viteză.
| Viteză | Viteză | |
| Definiție | Este distanța parcursă pe unitate de timp. | Este deplasarea (sau schimbarea poziției) în fiecare unitate de timp. |
| Notaţie | v | v |
| Tipul de obiect matematic | A urca. | Vector. |
| Formula (pentru o perioadă de timp finită) * | v = Δs / Δt | v = Δr / Δt |
| Formula (pentru un moment dat de timp) ** | v = ds / dt = s '(t) | v = dr / dt = r '(t) |
| Explicația formulei | * Lungimea căii parcurse împărțită la perioada de timp utilizată pentru a o parcurge. ** În viteza instantanee, perioada de timp tinde la zero. | * Deplasarea vectorială împărțită la intervalul de timp în care s-a produs deplasarea. |
| Caracteristici | Pentru a-l exprima, este necesar doar un număr real pozitiv, indiferent de dimensiunile spațiale în care are loc mișcarea.. | Poate dura mai mult de un număr real (pozitiv sau negativ) pentru a-l exprima, în funcție de dimensiunile spațiale în care are loc mișcarea.. |
Diferite aspecte ale vitezei și vitezei au fost rezumate în tabelul de mai sus. Și apoi, pentru a completa, sunt luate în considerare câteva exemple care ilustrează conceptele implicate și relațiile lor:
Să presupunem că o furnică roșie se mișcă de-a lungul unei linii drepte și în direcția indicată în figura de mai jos.
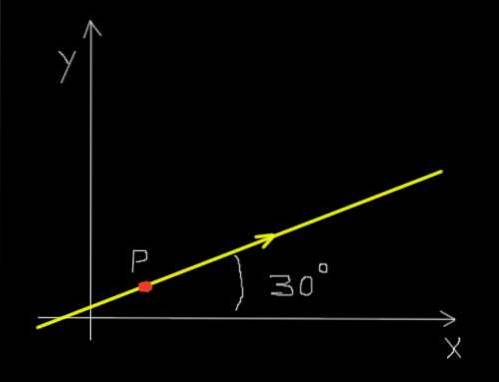
În plus, furnica se mișcă uniform, astfel încât să parcurgă o distanță de 30 milimetri într-o perioadă de timp de 0,25 secunde..
Determinați viteza și viteza furnicii.
Viteza furnicii se calculează împărțind distanța Δs a călătorit între intervalul de timp Δt.
v = Δs / Δt = (30 mm) / (0.25s) = 120 mm / s = 12 cm / s
Viteza furnicii se calculează prin împărțirea deplasării Δr între perioada de timp în care s-a făcut deplasarea menționată.
Deplasarea a fost de 30 mm în direcția de 30 ° față de axa X sau în formă compactă:
Δr = (30 mm ¦ 30º)
Se poate observa că deplasarea constă dintr-o mărime și o direcție, deoarece este o mărime vectorială. Alternativ, deplasarea poate fi exprimată în conformitate cu componentele sale carteziene X și Y, în acest fel:
Δr = (30 mm * cos (30º); 30 mm * sin (30º)) = (25,98 mm; 15,00 mm)
Viteza furnicii se calculează împărțind deplasarea la perioada de timp în care a fost realizată:
v = Δr/ Δt = (25,98 mm / 0,25 sec; 15,00 mm / 0,25 sec) = (103,92; 60,00) mm / sec
Această viteză în componentele carteziene X și Y și în unități de cm / s este:
v = (10,392; 6,000) cm / s.
Alternativ, vectorul vitezei poate fi exprimat în forma sa polară (modulul modul direcție) așa cum se arată:
v = (12 cm / s ¦ 30º).
Notă: în acest exemplu, deoarece viteza este constantă, viteza medie și viteza instantanee coincid. Se constată că modulul vitezei instantanee este viteza instantanee.
Aceeași furnică din exemplul anterior merge de la A la B, apoi de la B la C și în cele din urmă de la C la A, urmând calea triunghiulară prezentată în figura următoare.
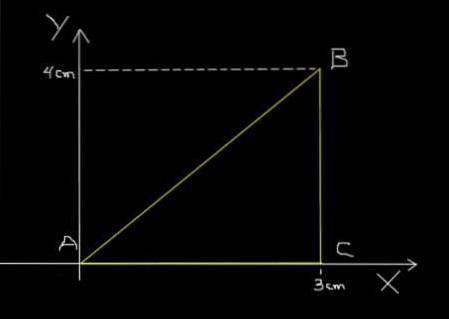
Secțiunea AB o acoperă în 0,2 secunde; BC îl traversează în 0,1 secunde și în cele din urmă CA îl traversează în 0,3 secunde. Calculați viteza medie a călătoriei ABCA și viteza medie a călătoriei ABCA.
Pentru a calcula viteza medie a furnicii, începem prin a determina distanța totală parcursă:
Δs = 5 cm + 4 cm + 3 cm = 12 cm.
Perioada de timp utilizată pentru întreaga călătorie este:
Δt = 0.2s + 0.1s + 0.3s = 0.6 s.
Deci, viteza medie a furnicii este:
v = Δs / Δt = (12 cm) / (0.6s) = 20 cm / s.
Apoi, se calculează viteza medie a furnicii în ruta ABCA. În acest caz, deplasarea făcută de furnică este:
Δr = (0 cm; 0 cm)
Acest lucru se datorează faptului că decalajul este diferența dintre poziția finală minus poziția inițială. Deoarece ambele poziții sunt aceleași, atunci diferența lor este nulă, rezultând o deplasare nulă.
Această deplasare nulă a fost efectuată într-o perioadă de timp de 0.6s, deci viteza medie a furnicii a fost:
v =(0 cm; 0 cm) / 0.6s = (0; 0) cm / s.
Concluzie: viteza medie 20 cm / s, dar viteza medie este zero pe ruta ABCA.
O insectă se mișcă pe un cerc cu o rază de 0,2 m cu o viteză uniformă, astfel încât, începând de la A și ajungând la B, călătorește ¼ a unei circumferințe în 0,25 s.
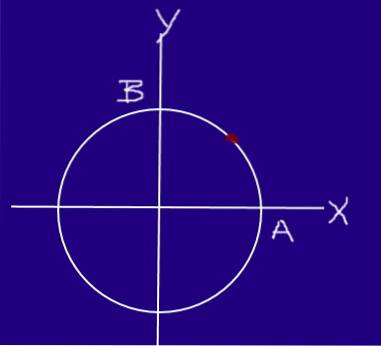
Determinați viteza și viteza insectei în secțiunea AB.
Lungimea arcului de circumferință dintre A și B este:
Δs = 2πR / 4 = 2π (0,2 m) / 4 = 0,32 m.
Aplicând definiția vitezei medii, avem:
v = Δs / Δt = 0,32 m / 0,25 s = 1,28 m / s.
Pentru a calcula viteza medie, este necesar să se calculeze vectorul de deplasare între poziția inițială A și poziția finală B:
Δr = (0, R) - (R, 0) = (-R, R) = (-0,2, 0,2) m
Aplicând definiția vitezei medii, obținem:
v = Δr/ Δt = (-0,2, 0,2) m / 0,25s = (-0,8, 0,8) m / s.
Expresia anterioară este viteza medie între A și B exprimată în formă carteziană. Alternativ, viteza medie poate fi exprimată sub formă polară, adică modul și direcție:
| v | = ((-0,8) ^ 2 + 0,8 ^ 2) ^ (½) = 1,13 m / s
Direcție = arctan (0,8 / (-0,8)) = arctan (-1) = -45º + 180º = 135º în raport cu axa X.
În cele din urmă, vectorul vitezei medii în formă polară este: v =(1,13 m / s ¦ 135º).
Presupunând că timpul de pornire al insectei din exemplul anterior este 0s de la punctul A, avem că vectorul său de poziție în orice moment t este dat de:
r(t) = [R cos ((π / 2) t); R sin ((π / 2) t)].
Determinați viteza și viteza instantanee pentru orice moment t.
Viteza instantanee este derivata în raport cu timpul funcției de poziție:
v(t) = dr/ dt = [-R (π / 2) sin ((π / 2) t); R (π / 2) cos ((π / 2) t)]
Viteza instantanee este modulul vectorului vitezei instantanee:
v (t) = | v(t) | = π R / 2 ^ ½
Nimeni nu a comentat acest articol încă.