
Formula ecuațiilor de gradul I, modul de rezolvare a acestora, exemplu, exerciții
ecuații de gradul I sau liniare cu o necunoscută sunt cele care pot fi exprimate ca suma a doi termeni, după cum urmează:
ax + b = 0
Unde a și b, cu la ≠ 0, sunt numere reale R sau, de asemenea, complexe C. Pentru a o rezolva, termenii sunt transpuși, ceea ce înseamnă schimbarea termenilor dintr-o parte a egalității în cealaltă.
Pentru a rezolva necunoscutul, se transpune termenul + b, care trebuie să meargă în partea dreaptă a egalității cu semnul schimbat.
topor = -b
Apoi, valoarea lui x este ștearsă, astfel:
x = - b / a
De exemplu, vom rezolva următoarea ecuație:
6x - 5 = 4
Transpunem termenul -5 în partea dreaptă cu un semn modificat:
6x = 4 + 5
Acest lucru este echivalent cu a adăuga 5 la ambele părți ale ecuației inițiale:
6x - 5 + 5 = 4 + 5 → 6x = 9
Și acum rezolvăm necunoscutul „x”:
x = 9/6 = 3/2
Ceea ce este echivalent cu împărțirea ambelor părți ale egalității la 6. Deci putem folosi următoarele pentru a obține soluția:
-Aceeași cantitate poate fi adăugată sau scăzută de pe ambele părți ale egalității într-o ecuație, fără a o modifica.
-De asemenea, puteți înmulți (sau împărți) cu aceeași cantitate toți termenii atât la stânga, cât și la dreapta ecuației.
-Și dacă ambii membri ai unei ecuații sunt ridicați la aceeași putere, nici egalitatea nu se modifică.
Indice articol
- 1 Cum se rezolvă ecuațiile de gradul I
- 1.1 Interpretarea grafică
- 2 Exemple de ecuații liniare simple
- 2.1 Ecuații întregi
- 2.2 Ecuații fracționare
- 2.3 Ecuații literale
- 2.4 Sisteme de ecuații de gradul I
- 2.5 Ecuații liniare cu valoare absolută
- 3 exerciții simple rezolvate
- 3.1 - Exercițiul 1
- 3.2 - Exercițiul 2
- 3.3 - Exercițiul 3
- 4 Referințe
Cum se rezolvă ecuațiile de gradul I
Soluția unei ecuații de gradul întâi este cunoscută și sub numele de rădăcină. Valoarea lui x transformă expresia originală într-o egalitate. De exemplu în:
5x = 8x - 15
Dacă substituim x = 5 în această ecuație, obținem:
5⋅5 = 8⋅5 - 15
25 = 40 - 15
25 = 25
Deoarece ecuațiile liniare de gradul întâi vin în multe forme, care uneori nu sunt evidente, există o serie de reguli generale care includ diverse manipulări algebrice, pentru a găsi valoarea necunoscutului:
-În primul rând, dacă există operațiuni indicate, acestea ar trebui efectuate.
-Simbolurile de grupare, cum ar fi parantezele, parantezele pătrate și parantezele, dacă există, ar trebui eliminate, păstrând semnele corespunzătoare.
-Termenii sunt transpuși pentru a plasa pe toți cei care conțin necunoscutul pe o parte a egalității, iar cei care nu o conțin pe cealaltă.
-Apoi, toți termenii similari sunt reduși pentru a ajunge la formular topor = -b.
-Și ultimul pas este să ștergi necunoscutul.
Interpretare grafică
Ecuația de primul grad ridicată la început poate fi derivată din ecuația liniei y = mx + c, făcând y = 0. Valoarea rezultată a lui x corespunde intersecției liniei cu axa orizontală.
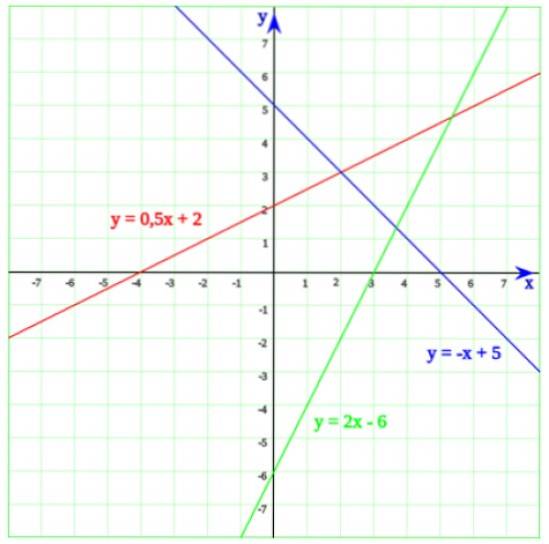
În figura următoare sunt trei linii. Începând cu linia verde, a cărei ecuație este:
y = 2x - 6
Făcând y = 0 în ecuația liniei se obține ecuația de gradul I:
2x - 6 = 0
A cărei soluție este x = 6/2 = 3. Acum, când detaliem graficul, este ușor să ne dăm seama că, de fapt, linia intersectează axa orizontală la x = 3.
Linia albastră intersectează axa x la x = 5, care este soluția la ecuația -x + 5 = 0. În cele din urmă, linia a cărei ecuație este y = 0,5x + 2 intersectează axa x la x = - 4 , care este ușor de văzut din ecuația primului grad:
0,5 x + 2 = 0
x = 2 / 0,5 = 4
Exemple de ecuații liniare simple
Ecuații întregi
Sunt aceia în termenii cărora nu există numitori, de exemplu:
21 - 6x = 27 - 8x
Soluția dvs. este:
-6x + 8x = 27 - 21
2x = 6
x = 3
Ecuații fracționare
Aceste ecuații conțin cel puțin un numitor diferit de 1. Pentru a le rezolva, este recomandabil să înmulțim toți termenii cu cel mai mic multiplu comun (MCM) al numitorilor, pentru a-i elimina.
Următoarea ecuație este de tip fracționar:

Deoarece aceste numere sunt mici, nu este dificil să vedem că m.c.m (6, 8,12) = 24. Acest rezultat se obține cu ușurință prin exprimarea numerelor ca produs al numerelor prime sau al puterilor lor, să vedem:
6 = 3,2
8 = 23
12 = 2Două⋅3
Cel mai mic multiplu comun este determinat de înmulțirea factorilor comuni și neobișnuiți de 6, 8 și 12 cu cel mai mare exponent al lor, apoi:
mcm (6,8,12) = 23 ⋅3 = 8 × 3 = 24
Deoarece avem cel mai mic multiplu comun, acesta trebuie înmulțit cu fiecare dintre termenii ecuației:

4 (x + 5) -3 (2x + 3) = 2 (1-5x)
Facem uz de proprietatea distributivă:
4x + 20 - 6x -9 = 2 - 10x
Toți termenii care conțin „x” necunoscut sunt grupați pe partea stângă a egalității, lăsând termenii independenți sau numerici pe partea dreaptă:
4x - 6x + 10 x = 2 +9 - 20
8x = -9
x = - 9/8
Ecuații literale
Sunt ecuații liniare cu o singură necunoscută, care totuși sunt însoțite de coeficienți literali (litere). Aceste litere sunt tratate la fel ca numerele. Un exemplu de ecuație literală de primul grad este:
-3ax + 2a = 5x - b
Această ecuație este rezolvată în același mod ca și cum termenii și coeficienții independenți ar fi numerici:
-3ax - 5x = - b - 2a
Factorizarea „x” necunoscut:
x (-3a - 5) = - b - 2a
x = (- b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)
Sisteme de ecuații de gradul I
Sistemele de ecuații constau dintr-un set de ecuații cu două sau mai multe necunoscute. Soluția sistemului constă în valori care satisfac ecuațiile simultan și pentru a o determina fără echivoc, trebuie să existe o ecuație pentru fiecare necunoscut.
Forma generală a unui sistem de m ecuații liniare cu n necunoscute sunt:
launsprezeceX1 + la12XDouă +… la1nXn = b1
ladouăzeci și unuX1 + la22XDouă +… la2nXn = bDouă
...
lam1X1 + lam2XDouă +… lamnXn = bm
Dacă sistemul are o soluție, se spune că este compatibil determinat, atunci când există un set infinit de valori care îl satisfac este compatibil nedeterminat, și, în cele din urmă, dacă nu are nicio soluție, atunci este incompatibil.
În rezolvarea sistemelor de ecuații liniare, se utilizează mai multe metode: reducerea, substituția, egalizarea, metodele grafice, eliminarea Gauss-Jordan și utilizarea determinanților sunt printre cele mai utilizate. Dar există și alți algoritmi pentru a ajunge la soluție, mai convenabili pentru sistemele cu multe ecuații și necunoscute.
Un exemplu de sistem de ecuații liniare cu două necunoscute este:
8x - 5 = 7y - 9
6x = 3y + 6
Soluția acestui sistem este prezentată mai târziu în secțiunea de exerciții rezolvate..
Ecuații liniare cu valoare absolută
Valoarea absolută a unui număr real este distanța dintre locația sa pe linia numerică și 0 pe linia numerică. Deoarece este o distanță, valoarea ei este întotdeauna pozitivă.
Valoarea absolută a unui număr este notată de barele modulo: │x│. Valoarea absolută a unui număr pozitiv sau negativ este întotdeauna pozitivă, de exemplu:
│ + 8│ = 8
│-3│ = 3
Într-o ecuație a valorii absolute, necunoscutul se află între barele de modul. Să luăm în considerare următoarea ecuație simplă:
│x│ = 10
Există două posibilități, prima este că x este un număr pozitiv, caz în care avem:
x = 10
Și cealaltă posibilitate este că x este un număr negativ, în acest caz:
x = -10
Acestea sunt soluțiile acestei ecuații. Acum să vedem un alt exemplu:
│x + 6│ = 11
Cantitatea din interiorul barelor poate fi pozitivă, deci:
x + 6 = 11
x = 11 -6 = 5
Sau poate fi negativ. În acest caz:
-(x + 6) = 11
-x - 6 = 11 ⇒ -x = 11 + 6 = 17
Și valoarea necunoscutului este:
x = -17
Această ecuație a valorii absolute are, prin urmare, două soluții: x1 = 5 și xDouă = -17. Putem verifica dacă ambele soluții conduc la o egalitate în ecuația inițială:
│5 + 6│ = 11
│11│ = 11
Da
│-17 + 6│ = 11
│-11│ = 11
Exerciții simple rezolvate
- Exercitiul 1
Rezolvați următorul sistem de ecuații liniare cu două necunoscute:
8x - 5 = 7y -9
6x = 3y + 6
Soluţie
După cum se propune, acest sistem este ideal pentru utilizarea metodei de substituție, deoarece în a doua ecuație necunoscutul X este aproape gata de autorizare:
x = (3y + 6) / 6
Și poate fi imediat substituit în prima ecuație, care apoi devine o ecuație de gradul întâi cu „y” necunoscut:
8 [(3y + 6) / 6] - 5 = 7y - 9
Numitorul poate fi eliminat înmulțind fiecare termen cu 6:
6. 8⋅ [(3y + 6) / 6] - 6,5 = 6 .7y- 6. 9
8⋅ (3y + 6) - 30 = 42y - 54
Aplicarea proprietății distributive în primul termen la dreptul de egalitate:
24y + 48 -30 = 42y - 54 ⇒ 24y + 18 = 42y - 54
Ecuația poate fi simplificată, deoarece toți coeficienții sunt multipli ai lui 6:
4y + 3 = 7y - 9
-3y = -12
y = 4
Cu acest rezultat mergem la compensarea lui x:
x = (3y +6) / 6 → x = (12 + 6) / 6 = 3
- Exercițiul 2
Rezolvați următoarea ecuație:
Soluţie
Produsele apar în această ecuație și urmând instrucțiunile date la început, acestea trebuie dezvoltate mai întâi:
3x - 10x +14 = 5x + 36x + 12
Apoi, toți termenii care conțin necunoscutele sunt duse în partea stângă a egalității, iar în partea dreaptă vor fi termenii independenți:
3x - 10x - 5x - 36x = 12-14
-48x = -2
x = 1/24
- Exercițiul 3
Adăugarea celor trei unghiuri interioare ale unui triunghi dă 180º. Maiorul îl depășește pe minor cu 35 °, iar acesta din urmă depășește la rândul său cu 20 ° diferența dintre major și mediu. Care sunt unghiurile?
Soluţie
Vom numi „x” unghiul mai mare, „y” cel din mijloc și „z” cel mai mic. Când declarația afirmă că suma acestora este de 180º, se poate scrie:
x + y + z = 180
Atunci știm că cu cât depășește cel mai mic cu 35º, putem scrie acest lucru astfel:
x = z + 35
În cele din urmă, cel mai mic depășește diferența dintre cel mai mare și mijloc cu 20 °:
z = x - y + 20
Avem un sistem de 3 ecuații și 3 necunoscute:
x + y + z = 180
x = z + 35
z = x - y + 20
Rezolvând pentru z din prima ecuație avem:
z = 180 - x - y
Potrivit cu al treilea:
180 - x - y = x - y + 20
Trecerea necunoscutelor în partea stângă ca întotdeauna:
-x - y - x + y = 20 - 180
„Y” este anulat și rămâne:
-2x = - 160
x = 80º
Din a doua ecuație găsim valoarea lui z:
z = x - 35 = 80 - 35 = 45º
Și valoarea lui y se găsește din prima sau a treia:
y = 180 - x - z = 180 - 80 - 45 = 55º
Referințe
- Baldor. 1977. Algebra elementară. Ediții culturale venezuelene.
- Institutul Monterey. Ecuații, inegalități și valoare absolută. Recuperat de pe: montereyinstitute.org.
- Profesor online. Clasificarea ecuațiilor liniare sau de gradul I. Recuperat de la: profesorenlinea.cl.
- Hoffman, J. Selecția subiectelor de matematică. Volumul 2.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Zill, D. 1984. Algebră și trigonometrie. Dealul Mcgraw.



Nimeni nu a comentat acest articol încă.