
Caracteristicile oglinzii concavă, exemple, aplicații

Oglindă concavă sau convergent este o oglindă cu o formă sferică aproape întotdeauna, în care suprafața reflectantă se află pe partea interioară a sferei sau mai degrabă o parte a acesteia. Sunt posibile și alte forme curbate, cum ar fi parabola.
Cu oglinzile curbate, precum oglinda concavă, este posibil să se realizeze diverse imagini: mărite, diminuate sau chiar inversate. Imaginile mărite facilitează vizualizarea detaliilor fine ale unui obiect.

Într-o oglindă concavă, mărirea se realizează deoarece curbura permite luminii să se concentreze în același mod ca și un obiectiv..
Oglinda funcționează așa cum se arată în figura de mai sus. Razele de lumină orizontale incidente provin din stânga, unde există o sursă îndepărtată, cum ar fi Soarele. Aceste raze îndeplinesc legea reflecției, care afirmă că unghiul de incidență al razei de lumină este egal cu unghiul său de reflexie..
După ce sunt reflectate, razele se intersectează într-un punct special, punctul F sau Punct focal, pentru că acolo este focalizată lumina. Plasând obiecte în diferite locații pe axa care trece prin C, F și V, se obțin diferitele imagini.
De exemplu, între punctul focal și vârful oglinzii este locul ideal pentru a plasa fața atunci când aplici machiaj sau bărbierit, deoarece în acest fel se obține o imagine cu detalii deosebite care nu este posibilă cu o oglindă plană..
Indice articol
- 1 Caracteristicile unei oglinzi concavă
- 1.1 Metoda grafică
- 2 Exemple de oglinzi concave
- 2.1 Obiect între F și V
- 2.2 Obiect între C și F
- 2.3 Obiect dincolo de centru
- 3 Mărire laterală
- 4 Aplicații ale oglinzilor concave
- 4.1 Oglinzi de mărire
- 4.2 Telescop optic cu reflexie
- 4.3 Oglinzi dentare
- 4.4 Faruri auto
- 4.5 Concentratoare solare
- 5 Subiecte de interes
- 6 Referințe
Caracteristicile unei oglinzi concavă
Înainte de a vedea cum se formează imaginea, analizăm cu atenție punctele și distanțele prezentate în această ilustrație:
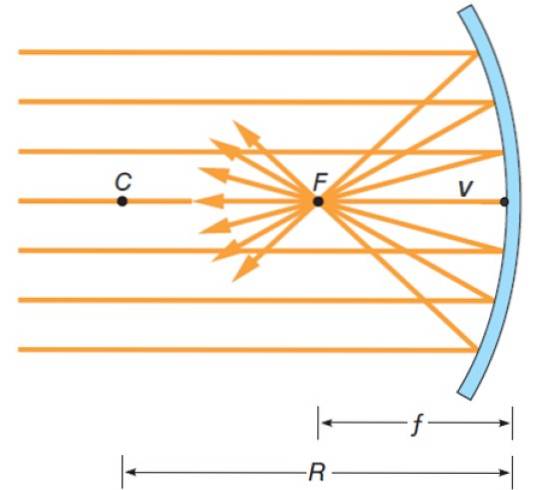
-Centrul sferei căreia îi aparține oglinda este în punctul C, iar R este raza sa. Punctul C este cunoscut sub numele de centrul de curbură iar R este Raza de curbură.
-Punctul V este vârf a oglinzii.
-Linia care unește punctele C, F și V este cunoscută sub numele de axa optică a oglinzii și este perpendiculară pe suprafața acesteia. O rază care lovește trecând prin aceste puncte se reflectă în aceeași direcție și în direcția opusă..
-Reflecția razelor incidente paralele cu axa optică se intersectează în punctul F, numit Punct focal a oglinzii.
-Rețineți că punctul F este aproximativ la jumătatea distanței dintre C și V.
-La distanța dintre F și V, notată ca F, se numeste distanța focală și se calculează ca:
f = R / 2
Metoda grafică
Așa cum am spus mai devreme, în funcție de punctul în care este plasat obiectul, se obțin mai multe imagini, care sunt ușor vizualizate prin metoda grafică pentru oglinzi..
Această metodă constă în trasarea razelor de lumină provenind din punctele strategice ale obiectului și observarea modului în care acestea sunt reflectate în suprafața speculară. Imaginea este obținută prin prelungirea acestor reflexii și privirea unde se intersectează.
În acest fel se știe dacă imaginea este mai mare sau mai mică, reală sau virtuală - dacă este formată în spatele oglinzii - și dreaptă sau inversată.
Exemple de oglinzi concave
Să vedem câteva exemple de imagini obținute folosind oglinzi concavă:
Obiect între F și V
Plasând obiectul între punctele F și V putem obține o imagine virtuală amplificată. Pentru a-l vizualiza, sunt trasate trei raze principale, așa cum se arată în ilustrația de mai jos:
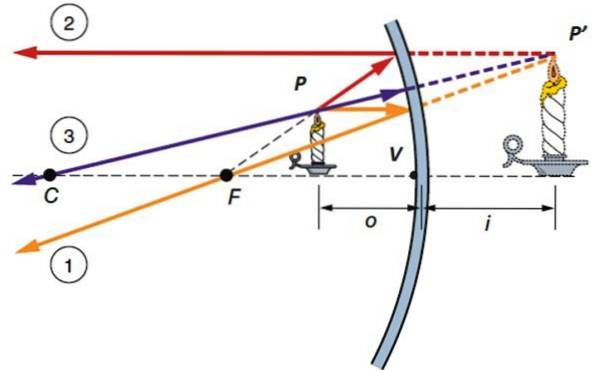
-Raza 1, care lasă flacăra în punctul P, este paralelă cu axa optică și se reflectă prin F.
-Raza 2: lovește în așa fel încât să fie reflectată într-o direcție paralelă cu axa optică.
-În cele din urmă, raza 3, care este radială, ajunge perpendicular pe oglindă și se reflectă în direcția opusă, trecând prin C.
Rețineți că legea reflexiei este îndeplinită la fel ca în oglinda plană, cu diferența că normalul de la suprafața oglinzii curbe se schimbă continuu.
De fapt, două raze sunt suficiente pentru a localiza imaginea. În acest caz, prin prelungirea celor trei raze, toate se intersectează într-un punct P 'din spatele oglinzii, care este locul în care se formează imaginea. Această imagine este virtuală - în realitate nu este traversată de nicio rază de lumină -, este verticală și este, de asemenea, mai mare decât originalul.
Obiect între C și F
Când obiectul se află între punctul focal și centrul de curbură al oglinzii, imaginea care se formează este reală - nu se află în spatele oglinzii, ci în fața ei - este mărită și inversată..
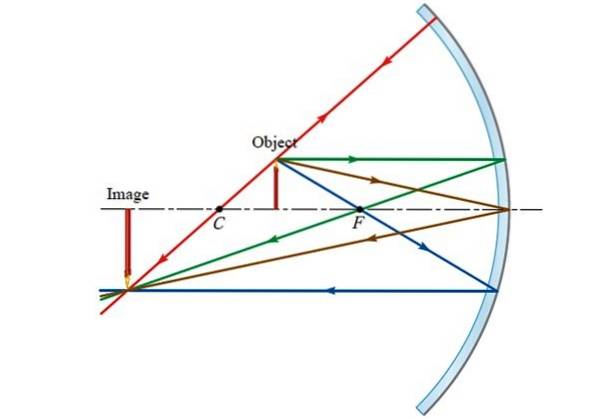
Obiectează dincolo de centru
Ilustrația de mai jos prezintă imaginea formată de un obiect departe de centrul oglinzii. Imaginea este formată în acest caz între punctul focal F iar centrul de curbură C. Este o imagine reală, inversată și mai mică decât obiectul în sine.
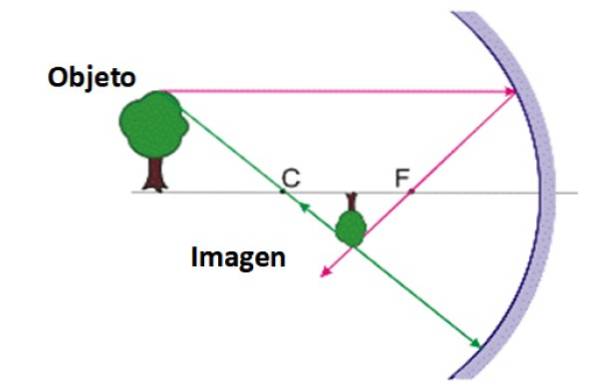
Mărire laterală
Ne putem întreba cât de amplificată sau diminuată este imaginea obținută prin intermediul oglinzii concavă, pentru aceasta mărire laterală, notat ca m. Este dat de coeficientul dintre dimensiunea imaginii și dimensiunea obiectului:
m = dimensiunea imaginii / dimensiunea obiectului
Imaginea formată dintr-o oglindă poate fi mai mică decât dimensiunea obiectului, chiar și așa, m este încă numit mărire sau crește latură.
Aplicații oglindă concavă
Proprietatea oglinzilor concave de a mări imaginile este utilizată în aplicații importante, de la îngrijire până la obținerea de energii curat.
Oglinzi de mărire

Acestea sunt utilizate în mod obișnuit în masa de toaletă în scopuri de îngrijire: machiaj, bărbierit și legarea unei cravate.
Telescop optic de reflexie
Primul telescop reflectorizant a fost creat de Isaac Newton și folosește o oglindă concavă plus un ocular. Una dintre oglinzile telescopice de tip Cassegrain este concavă și parabolică și este utilizată pentru a colecta lumina la punctul focal.
Oglinzi dentare

Stomatologii folosesc, de asemenea, oglinzi concavă pentru a obține o imagine mărită a dinților, astfel încât să poată examina dinții și gingiile cât mai detaliat posibil..
Faruri auto
În farurile auto, filamentul becului este plasat în punctul focal al unei oglinzi concavă. Razele de lumină provenite din filament sunt reflectate într-un fascicul de raze paralele.
Oglinda este adesea sferică, dar uneori se folosește forma parabolică, care are avantajul de a reflecta într-un fascicul paralel toate razele care provin de la punctul focal și nu numai cele care sunt aproape de axa optică..
Concentratoare solare
Lumina dintr-o sursă îndepărtată precum Soarele poate fi focalizată pe un punct de oglinda concavă. Datorită acestui fapt, căldura este concentrată în acel moment. La scară largă, cu această căldură se poate încălzi un fluid, cum ar fi apa sau uleiul de exemplu.
Acesta este concentrarea energiei solare termice care încearcă să producă energie electrică activând o turbină alimentată de căldura concentrată a Soarelui la un moment dat. Este o procedură alternativă la celula fotovoltaică semiconductoare.
Teme de interes
Oglindă convexă.
Referințe
- Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
- Giambattista, A. 2010. Fizică. Al 2-lea. Ed. McGraw Hill.
- Sala de clasă de fizică. Diagrame cu raze pentru oglinzi concavă. Recuperat de pe: physicsclassroom.com.
- Thomas, W. 2008. Fizică conceptuală. Dealul Mcgraw.
- Tippens, P. 2011. Fizică: concepte și aplicații. Ediția a VII-a. Dealul Mcgraw.


Nimeni nu a comentat acest articol încă.