
Coeficient de frecare static, exemplu, exercițiu

frecare statică este forța care apare între două suprafețe atunci când o suprafață nu alunecă față de cealaltă. Este de o mare importanță, deoarece ne permite să mergem înainte când mergem, deoarece este forța prezentă între podea și talpa pantofilor.
De asemenea, fricțiunea statică apare între trotuar și anvelopele mașinii. Dacă această forță nu este prezentă, atunci este imposibil ca mașina să înceapă să se miște, așa cum se întâmplă într-o mașină care încearcă să pornească pe o suprafață înghețată: roțile alunecă, dar mașina nu se mișcă.

Fricțiunea statică depinde de rugozitatea suprafețelor în contact și, de asemenea, de tipul de material din care sunt fabricate. De aceea anvelopele și pantofii sport sunt din cauciuc, pentru a crește frecarea cu trotuarul..
În modelul de frecare statică, caracteristicile materialelor și gradul de rugozitate dintre suprafețe sunt rezumate într-un număr numit coeficient de frecare static, care se determină experimental.
Indice articol
- 1 Coeficientul de frecare static
- 2 Exemplu: determinarea coeficientului de frecare static
- 3 Exercițiu
- 3.1 Soluție
- 4 Referințe
Coeficient de frecare static

Figura de mai sus prezintă o carte care este odihnită pe o masă cu o înclinație de 15,7º.
Dacă suprafețele cărții și ale mesei erau foarte netede și lustruite, cartea nu putea sta nemișcată. Dar, deoarece nu sunt, apare o forță care este tangentă la suprafețele în contact numite forța lui frecare statică.
Dacă unghiul de înclinare este suficient de mare, atunci nu este suficient forța de frecare statică pentru a echilibra cartea și ar începe să alunece.
În acest caz, există și frecare între carte și masă, dar asta ar fi un puterea de fricțiune dinamică, numit si frecare cinetică.
Există o graniță între fricțiunea statică și fricțiunea dinamică, care are loc în momentul în care fricțiunea statică atinge valoarea maximă.
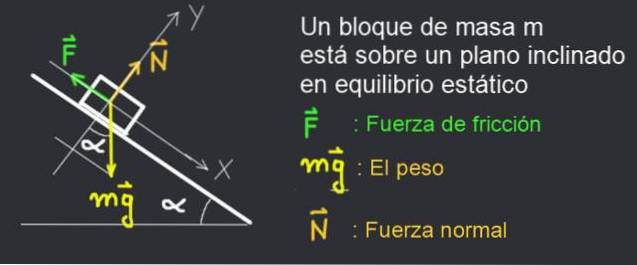
Să luăm în considerare în figura 2, diagrama forței unei cărți de masă m care este ținută în repaus pe un plan de înclinație α.
Cartea rămâne în repaus, deoarece forța de frecare statică F echilibrează sistemul.
Dacă unghiul de înclinare crește puțin, atunci suprafețele în contact trebuie să furnizeze mai multă forță de frecare, dar cantitatea de frecare statică pe care o pot furniza suprafețele în contact are o limită maximă Fmax, și anume:
F ≤ Fmax.
Forța maximă de frecare statică va depinde de materiale și de gradul de rugozitate al suprafețelor în contact, precum și de fermitatea prinderii.
Coeficientul static de frecare μși este un număr pozitiv care depinde de caracteristicile suprafețelor în contact. Forta normala N că planul exercită asupra blocului arată gradul de etanșeitate între suprafața blocului și planul. Acesta este modul în care determină forța maximă de frecare pe care o oferă suprafețele atunci când nu există alunecare:
Fmax = μși N
În rezumat, forța de frecare statică urmează următorul model:
F ≤ μși N
Exemplu: determinarea coeficientului de frecare static
Coeficientul de frecare static este un număr adimensional care se determină experimental pentru fiecare pereche de suprafețe.
Considerăm blocul în repaus în figura 2. Următoarele forțe acționează asupra acestuia:
- Forța de frecare: F
- Greutatea blocului de masă m: mg
- Forta normala: N
Deoarece blocul este în repaus și nu are nicio accelerație, conform celei de-a doua legi a lui Newton, forța rezultată - o sumă vectorială - este zero:
F + N + mg = 0
Un sistem fix de coordonate XY este considerat cu axa X de-a lungul planului înclinat și axa Y perpendiculară pe acesta, așa cum se arată în figura 2.
Forțele trebuie separate în funcție de componentele lor carteziene, dând naștere următorului sistem de ecuații:
-Componenta X: -F + mg Sen (α) = 0
-Componenta Y: N - mg Cos (α) = 0
Valoarea forței de frecare statică este rezolvată din prima ecuație:
F = mg Sen (α)
Și din a doua valoarea forței normale:
N = mg Cos (α)
Forța de frecare statică F respectă următorul model:
F ≤ μși N
Înlocuind valorile obținute anterior în inegalitatea avem:
mg Sen (α) ≤ μși mg Cos (α)
Luând în considerare faptul că pentru valori α cuprinse între 0º și 90º, funcțiile sinus și cosinus sunt ambele pozitive și că coeficientul dintre sinus și cosinus este tangent, avem:
Tan (α) ≤ μși
Egalitatea este valabilă pentru o anumită valoare a lui α numită unghiul critic și pe care o notăm cu α *, adică:
μși = Tan (α *)
Unghiul critic este determinat experimental, crescând înclinația treptat până la unghiul drept la care blocul începe să alunece, adică unghiul critic α *.
În cartea din figura 1, acest unghi a fost determinat experimental rezultând 24 °. Atunci coeficientul de frecare static este:
μși = Tan (24º) = 0,45.
Este un număr pozitiv între 0 și infinit. Dacă μși = 0 suprafețele sunt perfect netede. Dacă μși → ∞ suprafețele sunt perfect îmbinate sau sudate.
În general, valoarea coeficientului de frecare este între 0 și 10.
Exercițiu
În cursele de sprint sau dragster, se obțin accelerații de până la 4g în timpul startului, care se realizează tocmai atunci când anvelopele nu alunecă în raport cu trotuarul..
Acest lucru se datorează faptului că coeficientul de frecare static este întotdeauna mai mare decât coeficientul de frecare dinamic..
Presupunând că greutatea totală a vehiculului plus șoferul este de 600 kg și că roțile din spate suportă 80% din greutate, determinați forța de frecare statică în timpul startului de 4 g și coeficientul de frecare statică dintre anvelope și trotuar..

Soluţie
Conform celei de-a doua legi a lui Newton, forța rezultată este egală cu masa totală a vehiculului de câte ori accelerația pe care o dobândește.
Deoarece vehiculul se află în echilibru vertical, normalul și greutatea se anulează, lăsând ca forță rezultantă forța de frecare F pe care pavajul o exercită asupra zonei de contact a roților de tracțiune, lăsând astfel:
F = m (4g) = 600 kg (4 x 9,8 m / sDouă) = 23520 N = 2400 kg-f
Aceasta înseamnă că forța de tracțiune este de 2,4 tone.
Forța de frecare pe care o exercită roata pe sol merge înapoi, dar reacția sa, care este aceeași și opusă, acționează asupra anvelopei și merge înainte. Aceasta este forța care conduce vehiculul.
Desigur, toată această forță este produsă de motorul care încearcă să împingă podeaua înapoi prin roată, dar roata și podeaua sunt cuplate de forța de frecare.
Pentru a determina coeficientul de frecare statică folosim faptul că F obținut este fricțiunea maximă posibilă, deoarece ne aflăm la limita accelerației maxime, prin urmare:
F = μși N = μe (0,8 mg)
S-a luat în considerare faptul că roțile motoare spate suportă 0,8 ori greutatea. Rezolvând coeficientul de frecare, obținem:
μși = F / (0,8 mg) = 23520 N / (0,8 x 600 kg x 9,8 m / s ^ 2) = 5.
Concluzie: μși = 5.
Referințe
- Alonso M., Finn E. 1970. Fizica volumul I: Mecanică. Fondul Interamerican pentru Educație S.A.
- Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill.
- Hewitt, P. 2012. Științe fizice conceptuale. A cincea ediție.
- Rex, A. 2011. Fundamentele fizicii. Pearson. 190-200.
- Tânăr, Hugh. 2015. Fizică universitară cu fizică modernă. Ed. 14 Pearson.

Nimeni nu a comentat acest articol încă.