
Funcția omografică cum se grafizează, exerciții rezolvate
a mersion omografic sau rațional Este un tip de funcție matematică compusă din împărțirea a două componente polinomiale. Se supune formei P (x) / Q (x), unde Q (x) nu poate lua o formă nulă.
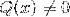
De exemplu, expresia (2x - 1) / (x + 3) corespunde unei funcții omografice cu P (x) = 2x - 1 și Q (x) = x + 3.

Funcțiile omografice constituie o secțiune de studiu a funcțiilor analitice, fiind tratate din abordarea grafică și din studiul domeniului și intervalului. Acest lucru se datorează restricțiilor și motivelor care trebuie aplicate pentru rezoluțiile lor..
Indice articol
- 1 Ce este o funcție omografică?
- 2 Funcție omografică mixtă
- 2.1 Chiar și a n-a rădăcină a funcției omografice
- 2.2 Logaritmul funcției omografice
- 3 Cum se grafizează o funcție omografică?
- 3.1 Rădăcini
- 3.2 Asimptotă verticală
- 3.3 Asimptotă orizontală
- 3.4 Intervalul de creștere
- 3.5 Interval de descompunere
- 3.6 Intersecția cu Y
- 4 Exemple
- 4.1 Exercițiul 1
- 4.2 Exercițiul 1.2
- 5 Exercițiul 2
- 6 Referințe
Ce este o funcție omografică?
Sunt expresii raționale ale unei singure variabile, deși acest lucru nu înseamnă că nu există o expresie similară pentru două sau mai multe variabile, unde ar fi deja în prezența corpurilor în spațiu care respectă aceleași tipare ca și funcția omografică din avionul.
Au rădăcini reale în unele cazuri, dar existența asimptotelor verticale și orizontale este întotdeauna menținută, precum și intervale de creștere și scădere. În mod obișnuit este prezentă doar una dintre aceste tendințe, dar există expresii capabile să le arate atât în dezvoltarea lor..
Domeniul său este restricționat de rădăcinile numitorului, deoarece nu există o divizare cu zero a numerelor reale.
Funcția omografică mixtă
Acestea sunt foarte frecvente în calcul, mai ales diferențiale și integrale, fiind necesare pentru a obține și antiderivide sub anumite formule. Unele dintre cele mai frecvente sunt clasificate mai jos.
Chiar și a n-a rădăcină a funcției omografice
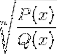
Excludeți toate elementele din domeniu care fac ca argumentul să fie negativ. Rădăcinile prezente în fiecare polinom valorile randamentului de zero atunci când sunt evaluate.
Aceste valori sunt acceptate de radical, deși trebuie luată în considerare restricția fundamentală a funcției omografice. În cazul în care Q (x) nu poate primi valori nule.
Soluțiile intervalelor trebuie interceptate:
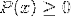
Pentru a obține soluția intersecțiilor, metoda semnelor poate fi utilizată, printre altele.
Logaritmul funcției omografice
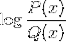
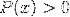
De asemenea, este comun să găsești ambele expresii într-una, printre alte combinații posibile.
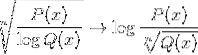
Cum se grafizează o funcție omografică?
Funcțiile omografice corespund grafic hiperbolelor din plan. Care sunt transportate orizontal și vertical conform valorilor care definesc polinoamele.
Există mai multe elemente pe care trebuie să le definim pentru a grafica o funcție rațională sau omografică.
Imobiliar
Prima va fi rădăcinile sau zerourile funcțiilor P și Q.
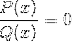
Valorile realizate vor fi notate pe axa x a graficului. Indicarea intersecțiilor grafului cu axa.
Asimptotă verticală
Ele corespund liniilor verticale, care delimitează graficul în funcție de tendințele pe care acestea le prezintă. Acestea ating axa x la valorile care fac numitorul zero și nu vor fi niciodată atinse de graficul funcției omografice.
Asimptotă orizontală
Reprezentată printr-o linie de cusătură orizontală, delimitează o limită pentru care funcția nu va fi definită la punctul exact. Tendințele vor fi observate înainte și după această linie.
Pentru a o calcula trebuie să recurgem la o metodă similară metodei L'Hopital, utilizată pentru a rezolva limitele funcțiilor raționale care tind spre infinit. Trebuie să luăm coeficienții celor mai mari puteri în numărătorul și numitorul funcției.
De exemplu, următoarea expresie are o asimptotă orizontală la y = 2/1 = 2.
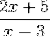
Interval de creștere
Valorile ordonate vor avea tendințe marcate pe grafic datorită asimptotelor. În cazul creșterii, funcția va crește în valori pe măsură ce elementele domeniului sunt evaluate de la stânga la dreapta.
Reduceți intervalul
Valorile ordonatei vor scădea pe măsură ce elementele domeniului sunt evaluate de la stânga la dreapta.
Salturile găsite în valori nu vor fi luate în considerare pe măsură ce crește sau scade. Acest lucru se întâmplă atunci când graficul este aproape de o asimptotă verticală sau orizontală, unde valorile pot varia de la infinit la infinit negativ și invers..
Intersecția Y
Prin setarea valorii lui x la zero, găsim interceptarea cu axa ordonată. Aceasta este o informație foarte utilă pentru obținerea graficului funcției raționale.
Exemple
Definiți graficul următoarelor expresii, găsiți rădăcinile lor, asimptotele verticale și orizontale, intervalele de creștere și scădere și intersecția cu axa ordonată.
Exercitiul 1
Expresia nu are rădăcini, deoarece are o valoare constantă în numărător. Restricția de aplicat va fi x diferit de zero. Cu asimptotă orizontală la y = 0 și asimptotă verticală la x = 0. Nu există puncte de intersecție cu axa y.
Se observă că nu există intervale de creștere chiar și cu saltul de la minus la plus infinit la x = 0.
Intervalul de descompunere este
ID: (-∞; o) U (0, ∞)
Exercițiul 1.2
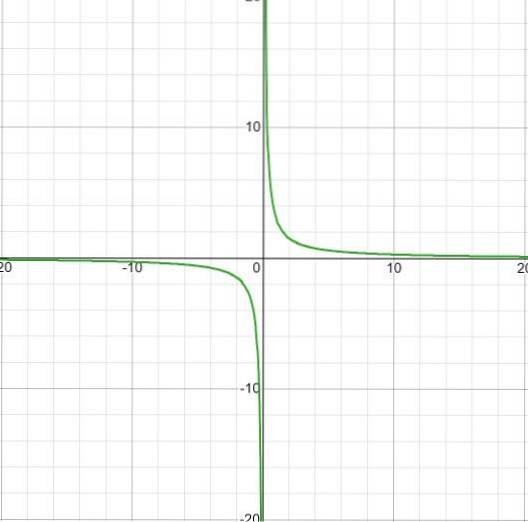
Se observă 2 polinoame ca în definiția inițială, deci procedăm în conformitate cu pașii stabiliți.
Rădăcina găsită este x = 7/2, care rezultă din setarea funcției egală cu zero.
Asimptota verticală este la x = - 4, care este valoarea exclusă din domeniu de condiția funcției raționale.
Asimptota orizontală este la y = 2, aceasta după împărțirea 2/1, coeficienții variabilelor de gradul 1.
Are o interceptare y = - 7/4. Valoare găsită după egalarea x la zero.
Funcția crește constant, cu un salt de la plus la minus infinit în jurul rădăcinii x = -4.
Intervalul său de creștere este (-∞, - 4) U (- 4, ∞).
Când valoarea lui x se apropie de minus infinit, funcția ia valori apropiate de 2. La fel se întâmplă atunci când x se apropie de mai mult infinit.
Expresia se apropie de plus infinit atunci când se evaluează la - 4 din stânga și la minus infinit atunci când se evaluează la - 4 din dreapta.
Exercițiul 2
Se observă graficul următoarei funcții omografice:
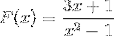
Descrieți comportamentul, rădăcinile, asimptotele verticale și orizontale, intervalele de creștere și scădere și intersecția cu axa ordonată..
Numitorul expresiei ne spune prin factorizarea diferenței de pătrate (x + 1) (x - 1) valorile rădăcinilor. În acest fel, ambele asimptote verticale pot fi definite ca:
x = -1 și x = 1
Asimptota orizontală corespunde axei absciselor, deoarece puterea cea mai mare este în numitor.
Singura sa rădăcină este definită de x = -1/3.
Expresia scade întotdeauna de la stânga la dreapta. Se apropie de zero când se apropie de infinit. Minus infinit pe măsură ce vă apropiați de -1 din stânga. Un infinit plus pe măsură ce se apropie de -1 din dreapta. Minus infinit când te apropii de 1 din stânga și mai mult infinit când te apropii de 1 din dreapta.
Referințe
- Aproximarea cu funcțiile raționale. Donald J. Newman. American Mathematical Soc., 31 dec. 1979
- Funcții raționale ortogonale. UNIVERSIDAD DE LA LAGUNA TENERIFE ADHEMAR BULTHEEL, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njastad. Cambridge University Press, 13 februarie. 1999
- Aproximarea rațională a funcțiilor reale. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 mar. 2011
- Funcții algebrice. Gilbert Ames Bliss. Courier Corporation, 1 ianuarie 2004
- Jurnalul Societății Matematice Spaniole, Volumele 5-6. Societatea spaniolă de matematică, Madrid 1916

Nimeni nu a comentat acest articol încă.