Gradele de libertate cum să le calculăm, tipuri, exemple

 grade de libertate în statistici sunt numărul de componente independente ale unui vector aleatoriu. Dacă vectorul are n componente și există p ecuații liniare care își raportează componentele, apoi grad de libertate este n-p.

Conceptul de grade de libertate Apare și în mecanica teoretică, unde aproximativ acestea sunt echivalente cu dimensiunea spațiului în care particula se mișcă, minus numărul de legături..

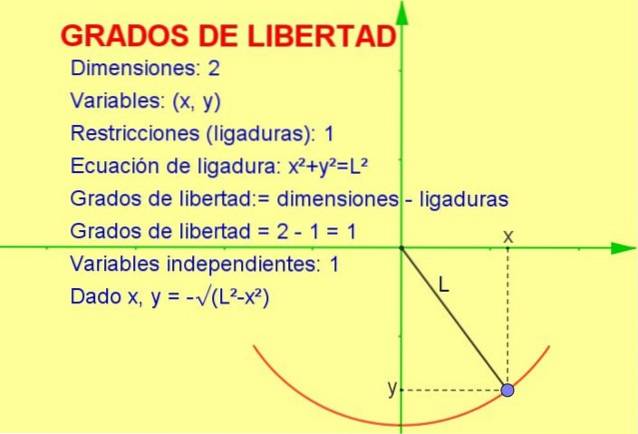
Acest articol va discuta conceptul de grade de libertate aplicat statisticilor, dar un exemplu mecanic este mai ușor de vizualizat sub formă geometrică.

Indice articol

• 1 Tipuri de grade de libertate
  • 1.1 Într-o carcasă mecanică
  • 1.2 Într-un set de valori aleatorii
• 2 Exemple
  • 2.1 Varianța și gradele de libertate
  • 2.2 În distribuția pătratului Chi
  • 2.3 În testarea ipotezelor (cu un exemplu elaborat)
• 3 Referințe

Tipuri de grade de libertate

În funcție de contextul în care este aplicat, modul de calcul al numărului de grade de libertate poate varia, dar ideea de bază este întotdeauna aceeași: dimensiunile totale minus numărul de restricții.

Într-o carcasă mecanică

Să luăm în considerare o particulă oscilantă legată de un șir (un pendul) care se deplasează în plan vertical x-y (2 dimensiuni). Cu toate acestea, particula este forțată să se deplaseze pe circumferința razei egale cu lungimea coardei.

Deoarece particula se poate deplasa numai pe acea curbă, numărul de grade de libertate este 1. Acest lucru poate fi văzut în figura 1.

Modul de a calcula numărul de grade de libertate este luând diferența dintre numărul de dimensiuni minus numărul de constrângeri:

grade de libertate: = 2 (dimensiuni) - 1 (ligatură) = 1

O altă explicație care ne permite să ajungem la rezultat este următoarea:

-Știm că poziția în două dimensiuni este reprezentată de un punct de coordonate (x, y).

-Dar întrucât punctul trebuie să satisfacă ecuația circumferinței (x^Două + Da^Două = L^Două) pentru o valoare dată a variabilei x, variabila y este determinată de respectiva ecuație sau restricție.

Astfel, doar una dintre variabile este independentă și sistemul are un (1) grad de libertate.

Într-un set de valori aleatorii

Pentru a ilustra ce înseamnă conceptul, să presupunem vectorul

X = (x₁, X_Două,..., X_n)

Ce reprezintă eșantionul n valori aleatorii distribuite în mod normal. În acest caz vectorul aleator X avea n componente independente și de aceea se spune că X avea n grade de libertate.

Acum să construim vectorul r de deșeuri

r = (x₁ - , X_Două - ,…., X_n - )

Unde reprezintă media eșantionului, care se calculează după cum urmează:

= (x₁ + X_Două +…. + X_n) / n

Deci suma

(X₁ - ) + (x_Două - ) + .... + (X_n - ) = (x₁ + X_Două +…. + X_n) - n= 0

Este o ecuație care reprezintă o constrângere (sau legare) asupra elementelor vectorului r din reziduuri, deoarece dacă sunt cunoscute n-1 componente ale vectorului r, ecuația de constrângere determină componenta necunoscută.

Prin urmare vectorul r de dimensiunea n cu restricția:

∑ (x_eu - ) = 0

Avea (n - 1) grade de libertate.

Se aplică din nou că calculul numărului de grade de libertate este:

grade de libertate: = n (dimensiuni) - 1 (constrângeri) = n-1

Exemple

Varianța și gradele de libertate

Varianța s^Două este definit ca media pătratului abaterilor (sau reziduurilor) eșantionului de n date:

s^Două = (r•r) / (n-1)

Unde r este vectorul reziduurilor r = (x1 - , x2 - ,…., Xn - ) și punctul gros (•) este operatorul de produs scalar. Alternativ, formula varianței poate fi scrisă după cum urmează:

s^Două = ∑ (x_eu - )^Două / (n-1)

În orice caz, trebuie remarcat faptul că atunci când se calculează media pătratului reziduurilor, acesta este împărțit la (n-1) și nu la n, deoarece, după cum sa discutat în secțiunea anterioară, numărul de grade de libertate al vector r este (n-1).

Dacă pentru calculul varianței s-au împărțit la n în loc de (n-1), rezultatul ar avea o prejudecată care este foarte semnificativă pentru valorile de n sub 50.

În literatură, formula varianței apare și cu divizorul n în loc de (n-1), când vine vorba de varianța unei populații.

Dar setul variabilei aleatorii a reziduurilor, reprezentat de vector r, Deși are dimensiunea n, are doar (n-1) grade de libertate. Cu toate acestea, dacă numărul de date este suficient de mare (n> 500), ambele formule converg la același rezultat.

Calculatoarele și foile de calcul oferă ambele versiuni ale varianței și abaterii standard (care este rădăcina pătrată a varianței).

Recomandarea noastră, având în vedere analiza prezentată aici, este să alegeți întotdeauna versiunea cu (n-1) de fiecare dată când este necesar să calculați varianța sau abaterea standard, pentru a evita rezultatele părtinitoare..

În distribuția pătratului Chi

Unele distribuții de probabilitate în variabile aleatoare continue depind de un parametru numit grad de libertate, este cazul distribuției Chi pătrat (χ^Două).

Numele acestui parametru provine tocmai din gradele de libertate ale vectorului aleatoriu subiacent căruia i se aplică această distribuție.

Să presupunem că avem g populații, din care sunt luate probe de mărime n:

X₁ = (x1₁, x1_Două,… X1_n)

X2 = (x2₁, x2_Două,… X2_n)

... .

X_j = (xj₁, xj_Două,… Xj_n)

... .

Xg = (xg₁, xg_Două,… Xg_n)

O populatie j ce are media și abaterea standard Sj, urmează distribuția normală N (, Sj ).

Variabila standardizată sau normalizată zj_eu este definit ca:

zj_eu = (xj_eu - ) / Sj.

Și vectorul Zj este definit astfel:

Zj = (zj₁, zj_Două,..., zj_eu,..., zj_n) și urmează distribuția normală normalizată N (0,1).

Deci variabila:

Π= ((z1₁ ^ 2 + z2₁^ 2 +…. + zg₁^ 2),…., (Z1_n^ 2 + z2_n^ 2 +…. + zg_n^ 2))

urmați distribuția χ^Două(g) numit distribuție chi pătrat cu grad de libertate g.

În testul de ipoteză (cu un exemplu elaborat)

Când doriți să testați ipoteze pe baza unui anumit set de date aleatorii, trebuie să cunoașteți numărul de grade de libertate g pentru a putea aplica testul Chi pătrat.

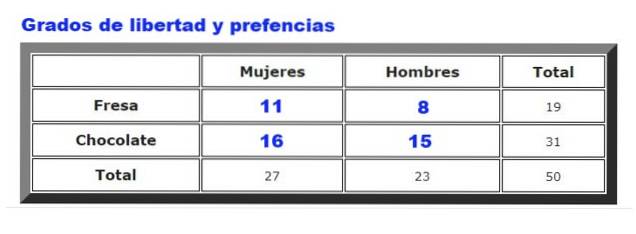
De exemplu, vor fi analizate datele colectate cu privire la preferințele înghețatei de ciocolată sau căpșuni în rândul bărbaților și femeilor dintr-o anumită înghețată. Frecvența cu care bărbații și femeile aleg căpșuna sau ciocolata este rezumată în figura 2.

În primul rând, se calculează tabelul frecvențelor așteptate, care este pregătit prin înmulțirea rânduri totale pentru el coloane totale, impartit de date totale. Rezultatul este prezentat în figura următoare:

Apoi continuăm să calculăm pătratul Chi (din date) folosind următoarea formulă:

χ^Două = ∑ (F_sau - F_și)^Două / F_și

Unde F_sau sunt frecvențele observate (Figura 2) și F_și sunt frecvențele așteptate (Figura 3). Suma merge peste toate rândurile și coloanele, care în exemplul nostru dau patru termeni.

După efectuarea operațiunilor, veți obține:

χ^Două = 0,2043.

Acum este necesar să comparăm cu pătratul teoretic Chi, care depinde de numărul de grade de libertate g.

În cazul nostru, acest număr este determinat după cum urmează:

g = (# rânduri - 1) (# coloane - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Se pare că numărul de grade de libertate g din acest exemplu este 1.

Dacă doriți să verificați sau să respingeți ipoteza nulă (H0: nu există nicio corelație între GUST și GEN) cu un nivel de semnificație de 1%, valoarea teoretică Chi-pătrat este calculată cu gradul de libertate g = 1.

Se caută valoarea care face ca frecvența acumulată (1 - 0,01) = 0,99, adică 99%. Această valoare (care poate fi obținută din tabele) este 6.636.

Deoarece Chi-ul teoretic îl depășește pe cel calculat, atunci se verifică ipoteza nulă.

Adică cu datele colectate, Neobservat relația dintre variabilele GUST și GEN.

Referințe

1. Minitab. Care sunt gradele de libertate? Recuperat de la: support.minitab.com.
2. Moore, David. (2009) Statistici de bază aplicate. Editor Antoni Bosch.
3. Leigh, Jennifer. Cum se calculează gradele de libertate în modelele statistice. Recuperat de pe: geniolandia.com
4. Wikipedia. Gradul de libertate (statistici). Recuperat de pe: es.wikipedia.com
5. Wikipedia. Gradul de libertate (fizic). Recuperat de pe: es.wikipedia.com